Put spreads
We’ll dive deep into put spreads in this chapter. As a reminder, a put spread is:
Long put & short put
Like call spreads, you should expect most math-based spread test questions to be on vertical (price) spreads, where the contracts have the same expiration but different strike prices. For example:
Short 1 ABC Jan 40 put
Long 1 ABC Jan 50 put
We’ll use the same four-step system used in the call spreads chapter to answer maximum gain, maximum loss, and breakeven questions. Again, this system only works with spreads, which is why it’s so important to identify strategies correctly.
Let’s go through the spread system together using this example:
Short 1 ABC Jan 40 put @ $5
Long 1 ABC Jan 50 put @ $11
Step 1: Net the premiums
The investor sold the short put for $5 and bought the long put for $11, creating a net debit (purchase) of $6, or $600 overall ($6 x 100 shares). This step determines the maximum gain or loss. Use this as your rule of thumb:
- Net debit = maximum loss
- Net credit = maximum gain
Because the investor had a net debit of $600, their maximum loss is $600.
Step 2: Net the strike prices
The second step is the only step that does not provide an answer. It will lead us to the other answers, though.
Short 1 ABC Jan 40 put @ $5
Long 1 ABC Jan 50 put @ $11
The difference between the two strike prices ($40 and $50) is $10.
Step 3: Net strikes - net premium
Take the difference between the strike prices ($10) and subtract the original net premium ($6). The difference is $4, which represents the “other max.” In step 1, we answered the maximum loss. Therefore, we’re finding the maximum gain in this step, which is $400 ($4 x 100 shares).
If step 1 determines the maximum loss, step 3 will answer the maximum gain. This applies in reverse also. If step 1 determines the maximum gain, step 3 will answer the maximum loss.
Step 4: Strike price +/- net premium
We must return to the original net premium determined in the first step ($6 debit) to find the breakeven. For the last step, you’ll use one of two processes, depending on whether it’s a call or put spread:
- Call spreads = add the net premium to the low strike
- Put spreads = subtract the net premium from the high strike
Short 1 ABC Jan 40 put @ $5
Long 1 ABC Jan 50 put @ $11
This is a put spread, so we’ll subtract the net premium ($6) from the high strike price ($50) to find breakeven at $44.
The options payoff chart can summarize the “big picture” of this long put spread. First, let’s re-establish the strategy:
Short 1 ABC Jan 40 put @ $5
Long 1 ABC Jan 50 put @ $11
Here’s the payoff chart:
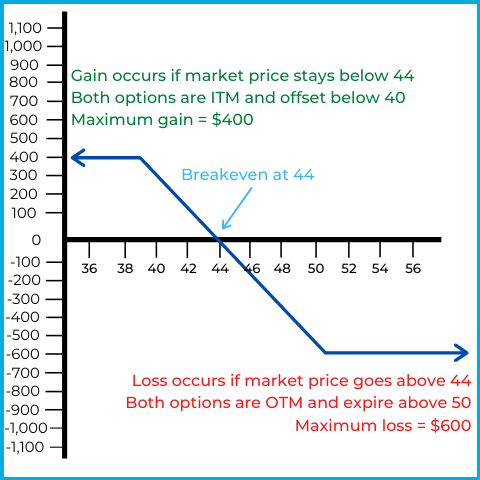
The horizontal axis represents the market price of ABC stock, while the vertical axis represents overall gain or loss.
- Maximum gain = $400
- Maximum loss = $600
- Breakeven = $44
- Option names = Long/bear/debit put spread
The investor is betting on a bear market, but also limited their gain potential. Let’s continue to analyze this strategy in a few phases:
If ABC’s market price stays above $50
Both options are “out of the money” and expire worthless, leaving the investor with their original net premium as their overall return. The net debit was $600, and that’s also the maximum loss.
If ABC’s market price goes below $50, but stays above $40
The long put goes “in the money” and gains intrinsic value. If ABC’s market price goes to $44, the long put gains $6 of intrinsic value, offsetting the $6 net debit and resulting in breakeven. The investor starts profiting below $44, as the long put gains more intrinsic value. The short put stays “out of the money” and expires as long as the market remains above $40.
If ABC’s market price goes below $40
Both options are “in the money” and begin offsetting each other. For every dollar gained on the long put as the market falls, a dollar is lost on the short put. The investor reaches their maximum gain at $40, but gains and losses are offset below $40.
What was the investor’s intent?
They were bearish on ABC’s market price but felt the long put’s premium ($1,100) was too expensive. Selling the other put for $500 reduces the net debit to $600. The option strategy is cheaper, but selling the put enforces a “floor” at $40. No matter how far the market falls, the short put offsets the long put’s gains below $40.
Let’s see if you can make it through an example on your own:
An investor goes long 1 XYZ Dec 30 put at $2 and short 1 XYZ Dec 45 put at $10. Answer the following:
Maximum loss?
Maximum gain?
Breakeven?
Names of the spread?
- Maximum loss = $700
- Maximum gain = $800
- Breakeven = $37
- Names of the spread = Short/bull/credit spread
This is how you can determine the answers:
Step 1: Net the premiums
Bought at $2 and sold at $10, creating a net credit of $8. Therefore, the maximum gain is $800
Step 2: Net the strike prices
The difference between $30 and $45 is $15.
Step 3: Net strikes - net premium
$15 (net strikes) - $8 (net premium) = $7. This represents the “other max” not found in the first step. The maximum gain was determined in step 1, so the maximum loss is $700.
Step 4: Strike price +/- net premium
This is a put spread, so we’ll subtract the $8 (net premium) from $45 (high strike price). Therefore, the breakeven is $37.
Naming the spread
We can utilize two methods to name this spread. First, the short put has the highest premium, making it the dominant leg. Also, it maintains the higher strike price, which is always the dominant leg on a vertical (price) put spread. With the short put being the dominant leg, this spread is a:
- Short put spread
- Bull put spread
- Credit put spread
The options payoff chart can summarize the “big picture” of this short put spread. First, let’s re-establish the strategy:
Long 1 XYZ Dec 30 put @ $2
Short 1 XYZ Dec 45 put @ $10
Here’s the payoff chart:
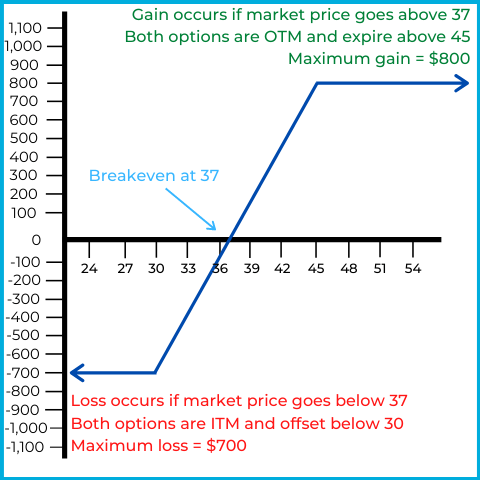
The horizontal axis represents the market price of ABC stock, while the vertical axis represents overall gain or loss.
- Maximum loss= $700
- Maximum gain = $800
- Breakeven = $37
- Option names = Short/bull/credit put spread
If XYZ’s market stays above $45
Both options are “out of the money” and expire worthless, resulting in the original net premium reflecting the investor’s overall return. The net credit was $800, which is also the maximum gain. This is why it’s a bull put spread - the investor prefers both options to expire so they can keep their initial net credit.
If XYZ’s market price goes below $45, but stays above $30
The short put goes “in the money” and begins gaining intrinsic value, which is not good for short options! When the market goes to $37, the short put loses $8 due to the option’s intrinsic value, offsetting the net credit and leading to breakeven. When the market goes below $37, the investor experiences an overall loss as the short put loses more value than the net credit received upfront. The long put stays “out of the money” and expires as long as XYZ’s market price remains above $30.
If XYZ’s market price goes below $30
Both options are “in the money” and begin offsetting each other. For every dollar lost on the short put as the market falls, a dollar is gained on the long put. Essentially, the long put “saves” the investor from losing more money.
What was the investor’s intent?
They were bullish on XYZ’s market price but wanted a hedge in case of a bear market. Buying the $200 put reduces the net credit to $800 (from $1,000). The investor receives a lower premium, but the investor’s loss potential is capped if the market price falls below $30.
Math-based spread questions on the exam tend to focus on the maximum gain, maximum loss, or breakeven. However, you may encounter other questions that test your general knowledge of spreads. For example:
An investor goes long 1 CBA Sep 70 put at $15 and short 1 CBA Sep 50 put at $4 when the market price is $60. The market goes to $52 and the investor closes the contracts at intrinsic value. What is the gain or loss?
Answer = $700 gain
| Action | Result |
|---|---|
| Buy put | -$1,500 |
| Sell put | +$400 |
| Close long put | +$1,800 |
| Close short put | $0 |
| Total | +$700 |
Initially, the investor buys the long put for $15 and sells the short put for $4, creating a net debit of $11 or $1,100 overall ($11 x 100 shares).
At $52, the long put is “in the money” (“put down”). To close the long put, the investor must perform a closing sale equal to the intrinsic value. The intrinsic value is $18 ($70 - $52), leading the investor to close the long put by selling it for $1,800.
At $52, the short put is “out of the money” and maintains no intrinsic value. To close the short put, the investor must perform a closing purchase equal to the intrinsic value. The intrinsic value is $0 (“out of the money”), leading the investor to close the short put by buying it for $0.
We have one last topic to cover in this chapter. Spread investors look for a specific outcome depending on whether the strategy is a debit or credit spread. Let’s start with what you need to know:
- Debit spreads = widen & exercise
- Credit spreads = narrow & expire
As we discussed in the call spreads chapter, you’ll likely answer every test question on this topic correctly if you know the word associations above. In most circumstances, you only need to know whether the strategy is a debit or credit spread.
In a debit spread, the investor hopes for the spread between the option premiums to widen. For example:
Short 1 ZYX Jan 20 put @ $1
Long 1 ZYX Jan 25 put @ $3
Market price = $24
The spread between the premiums is currently $2 ($3 - $1). This is a bear put spread (the long put has the higher premium and strike price), so the investor wants ZYX’s market price to fall.
If the market falls to $20, the long put’s premium will be at least $5, representing its intrinsic value. At $20, the short put still does not have intrinsic value. The short put premium could be approaching $0 if the option is about to expire. Let’s assume the long put’s premium is now $5, and the short put’s premium stays flat at $1. Now, the spread between the two premiums is $4 ($5 - $1), which is “wider” (bigger) than the original $2 spread. Now that the spread between the premiums has widened, the investor can close the contracts at a profit.
In a debit spread, the investor hopes for the options to exercise. Let’s use the same example:
Short 1 ZYX Jan 20 put @ $1
Long 1 ZYX Jan 25 put @ $3
Market price = $24
The investor is stuck with their original $200 net debit if both options expire, which is their maximum loss. This will occur if ZYX’s market price stays at or above $25. Obviously, the investor wants to avoid this scenario.
If ZYX’s market price falls below $25, the long put goes “in the money,” gains intrinsic value, and begins making a return for the investor. Once the market price declines below $20, the short put goes “in the money,” gains intrinsic value, and begins offsetting the long put’s gains.
If both options go “in the money” (when ZYX’s market price falls below $20), the investor is at their maximum gain. The long put is the investor’s “money maker,” and it’s the way the investor makes a profit with this call spread. Gains below $20 are negated due to the short put, but the investor still reaches their maximum gain if both options are “in the money” and get exercised.
For our last example, let’s take a look at credit spreads and how a test question on this topic may be tricky:
An investor goes long 1 LMN Jun 110 put and short 1 LMN Jun 125 put. Which of the following outcomes is the investor hoping for?
A) Spread between the premiums to widen and both options exercised
B) Spread between the premiums to narrow and both options expire
C) Spread between the premiums to widen and both options expire
D) Spread between the premiums to narrow and both options exercised
Answer = B
Premiums are not provided, but you can still determine the dominant leg on a vertical (price) put spread by identifying the option with the higher strike price. The short put has the highest strike price, making it the dominant leg. Therefore, the following names apply to this spread:
- Bull put spread
- Short put spread
- Credit put spread
Now that the spread is determined to be a credit spread, you can immediately identify the investor’s sentiment as narrow & expire.
If LMN’s market price rises above $125, both options go “out of the money” and have no intrinsic value. When this occurs, both option premiums will approach $0. We don’t know the original premiums, but we can assume the spread between them narrows as the premiums approach $0.
When the market price rises above the high strike price ($125), both options expire worthless, locking in the investor’s maximum gain. Therefore, it should be no surprise the investor prefers for both options to expire.
Whether you understand the context or not, here are the primary test points to know:
- Debit spreads = widen / exercise
- Credit spreads = narrow / expire
There are many memory tricks people use for this topic. For example, some remember the words credit, narrow, and expire all have six letters. The six-letter words all go together.
If you’re more of a visual learner, here’s a video combining all we’ve covered on put spreads:
Sign up for free to take 13 quiz questions on this topic