Triangles | Geometry | Achievable CLT

Introduction

Triangles questions are the largest single subcategory of questions (main categories being algebra, geometry, and math reasoning) on the CLT, forming at least some part of nearly 15% of CLT questions. Naturally, you should spend some extended time on this lesson! There are a number of formulas to memorize and properties to master; there are also important terms to define, such as the very frequent isosceles triangle. We have provided extra practice questions in this content area so you can spend plenty of time familiarizing yourself with the variety of triangle questions. As you work, make sure to sketch geometry figures on your scratch paper so you can add notations–especially if the question itself doesn’t give you a figure to start with!

Approach Question

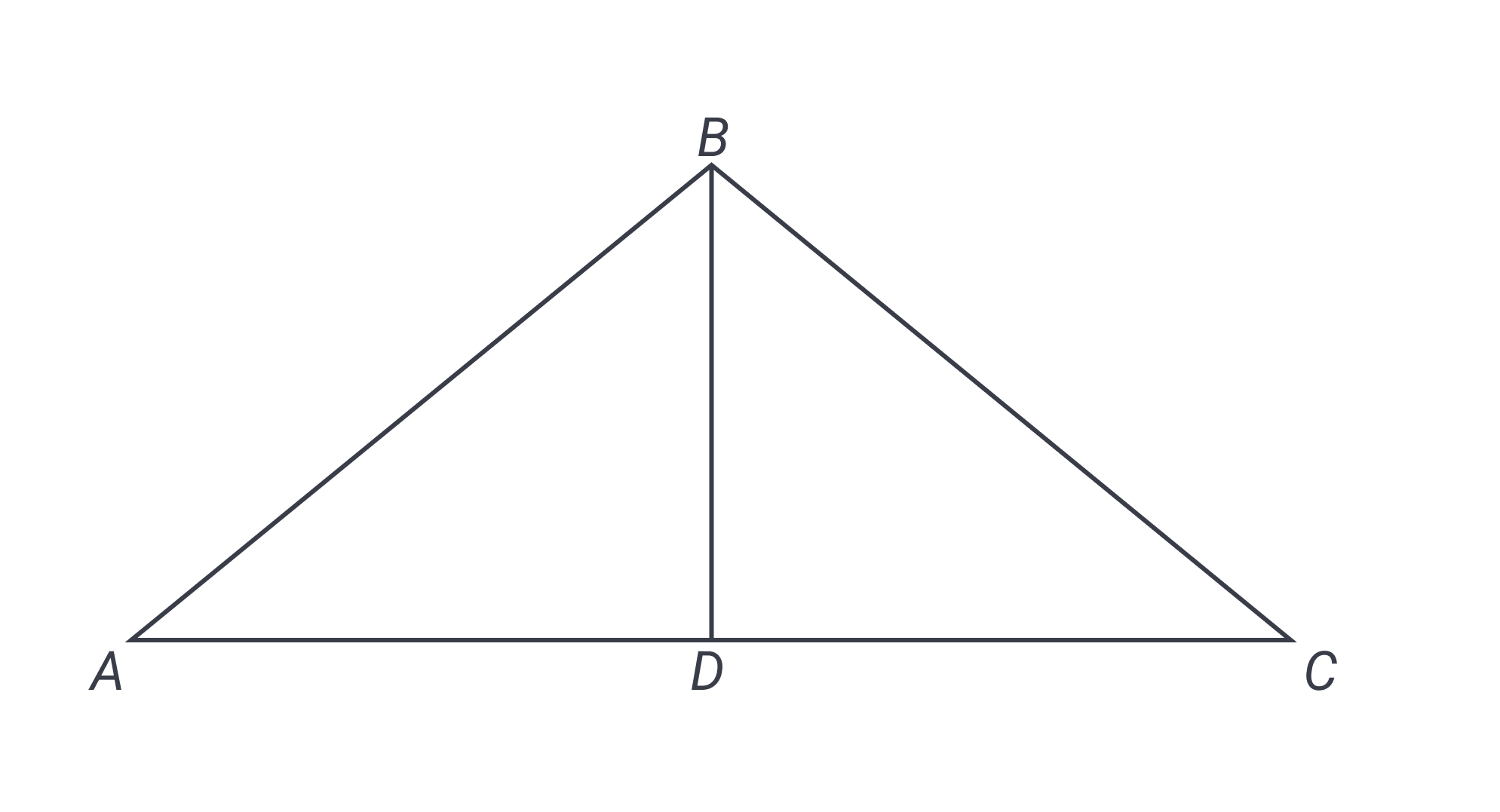
In the figure below, altitude BD is drawn within isosceles triangle ABC. If the length of BC is 15 and the length of AC, the longest side of the triangle, is three more than the length of AB, what is the area of the triangle? (Note: disregard units for this question.)

altitude BD drawn within isosceles triangle ABC

A. 72
B. 108
C. 144
D. 216

Explanation

This composite question tests our understanding of several related concepts, including area, isosceles triangles, and right triangles. We begin by copying the figure on our scratch paper so we can mark it up (except for the most basic questions, you should always copy the figure on geometry questions). Let’s label side $BC$ as $15$ . The objective is to get the area of the large triangle; given that the triangle area formula is (½)bh, we need to find the lengths of the base and height.

What else do we know? Two particularly important words are “isosceles” and “altitude”. Since an isosceles triangle has two equal sides, we should be able to use this information. But which two sides are congruent? We find our hint in the information given about side $A C$ ; since it is the longest side of the triangle, the other two sides must be the congruent pair. This means we can also label side $A B$ as $15$ . And while we’re at it, since that longest side $A C$ is three units longer than $A B$ , let’s label $A C$ as $18$ , perhaps using a bracket so it’s clear we’re labeling the whole base of the large triangle.

Meanwhile, an altitude is a line segment drawn from one vertex of a triangle and perpendicular to the opposite side. The altitude is equivalent to the height of the triangle if the side to which it is perpendicular is treated as the base. And because it is perpendicular, it makes right angles at point $D$ , so we know that triangles $A B D$ and $BC D$ are right triangles. Finally, since the large triangle is isosceles with equal sides on the left and right of the figure, the altitude must divide it evenly in half. So we can divide the base of 18 into two equal parts of $9$ .

We’re getting close to our goal! We know the base of $A BC$ is $18$ ; only the height remains unknown. Since we now have congruent right triangles on both left and right, we can use the Pythagorean theorem ( $a^{2} + b^{2} = c^{2}$ ) with either of these triangles to find the length of height $B D$ . We can say that $9^{2} + b^{2} = 1 5^{2}$ . With a little calculation (remember that we recommend learning all your multiples up to 15!), we get $b^{2} = 225 - 81 = 144$ , and if $b^{2} = 144$ then $b = 12$ . The height is $12$ . Don’t forget that our full base is $18$ , not $9$ ; we now enter the base and height into the area formula to discover that $(½) (12) (18) = 108$ . The answer is B.

Did you recognize anything about that right triangle? If you’ve learned anything about “Pythagorean triples” in geometry, you may have noticed a pattern that can streamline our process here. These “triples” are sets of three integers that satisfy the Pythagorean theorem. There are relatively few sets of three whole numbers that fit the theorem, so standardized tests will often emphasize the few that do. The most common is the $3 : 4 : 5$ triple. Notice from the colons (:) in between the numbers that we are describing a ratio; this means that while $3$ , $4$ , and $5$ can be the fixed lengths of a right triangle, multiples of the three numbers will also work. So $6$ , $8$ , and $10$ would be fine; $30$ , $40$ , and $50$ would fit as well; and our numbers here, $9$ , $12$ , and $15$ , if divided by $3$ , represent the $3 : 4 : 5$ ratio as well. So if you know your hypotenuse is $15$ and one of the triangle’s legs is $9$ , you can shorten your solving process by identifying 12 as the middle number in that ratio. We’ll include the most commonly used Pythagorean triples in this lesson; memorize them to speed up your approach to right triangle problems!

Definitions

Hypotenuse: The longest side of a right triangle; the side across from the right angle. Represented by $c$ in the Pythagorean theorem.
Leg: One of the shorter two sides of a right triangle. Represented by $a$ and $b$ in the Pythagorean theorem.
Altitude: A line segment drawn from one vertex of a triangle and meeting the opposite side at a right angle. The altitude also constitutes the height of a triangle, for purposes of calculating its area.
Isosceles: A triangle with two congruent sides and two congruent angles.
Equilateral: A triangle in which all three sides are congruent and all three angles are congruent. In an equilateral triangle, each angle measures 60°.
Scalene: A triangle in which no side is equal to any other, and therefore no angle is equal to any other.
Similar: A description of two or more triangles whose corresponding angle pairs are congruent, but whose corresponding sides (typically) are not. Two similar triangles, if drawn to scale, will look like copies of each other, with similar dimensions except that one is larger than the other. In similar triangles, corresponding sides are proportional, that is, these pairs of sides all share the same ratio of their lengths. This means that proportions are helpful algebra tools for working with similar triangles.
Congruent: Two shapes (in this case triangles) that are identical to each other in every way. Congruence can be proved by various theorems comparing their sides and angles; some notable examples are abbreviated SSS, SAS, AAS, and ASA.
Vertex: The points at which any two sides of a triangle meet; the “corners” of a triangle. A letter denoting the vertex of a triangle can also be used to the interior angle at that vertex.

Topics for Cross-Reference

Variations

Most of the variations of triangle problems involve triangles being drawn inside, or making up some part of, another shape. For example, a triangle might be inscribed in a circle–drawn so that all three of its vertices touch the circle. In this module, you’ll see an example wherein a triangle hidden inside a trapezoid helps us find the area of that trapezoid and another in which a hexagon is divided up into triangles to help us find its area. Triangles and quadrilaterals overlap quite a bit in standardized test questions; we’ll explore this confluence in the lesson on quadrilaterals.

Strategy Insights

Here’s a visual exercise. Place your hands together so that only the bases of your hands are touching, with your fingertips about an inch apart from each other (index finger an inch away from the other index finger, etc.). Notice how the angle created next to the base of your hands is rather small. Now, keeping the base of your hands together, spread out your hands so your right-hand fingers are several inches apart from your left-hand fingers. Do you see how the angle at the base of your hands grew much larger? This visual tells us an important truth: The size of an angle is related to the length of its opposite side, and vice versa. A small angle will correspond to a small side across from it, which is why the side across from the $30°$ angle must be the smallest in a $30 - 60 - 90$ triangle. A large angle corresponds to a large side across from it, which is why the hypotenuse must be the largest side in a right triangle: it is, by definition, across from the largest angle.
Much triangle work begins with knowing the right formulas. There are several triangle-related formulas provided in the CLT reference list; even though they are given to you on the test, we will reproduce them in the “Flashcard Fodder” section because we think you should memorize them anyway. That way you don’t have to take time consulting the reference box unless absolutely necessary.

Flashcard Fodder

Triangle formulas provided by the CLT on test day:

Area of a triangle = $½ (ba se) (h e i g h t)$

The sum of the measures of the interior angles of a triangle is $180°$ .

Pythagorean theorem for a right triangle: If $a$ , $b$ , and $c$ are the side lengths of the triangle, and $c$ is the hypotenuse, then $a^{2} + b^{2} = c^{2}$ .

$30° - 60° - 90°$ triangles have side lengths in a ratio of $1 : 3 : 2$ , corresponding to their opposite angle.

$45° - 45° - 90°$ triangles have side lengths in a ratio of $1 : 1 : 2$ , corresponding to their opposite angle.

Triangle formulas NOT provided by the CLT on test day:

Pythagorean triples:

$3 : 4 : 5$

$5 : 12 : 13$

$7 : 24 : 25$

$8 : 15 : 17$

Area of an equilateral triangle: $\frac{s ^{2} 3}{4}$ , where $s$ is the length of one side

$2$ is approximately 1.4.

$3$ is approximately 1.7.

Sample Questions

Note: since triangle problems are so frequent on the CLT, this set of practice exercises contains two questions for every difficulty instead of one.

Difficulty 1

A right triangle has one leg of length $12$ cm and a hypotenuse of $13$ cm. What is the length of its other leg, in cm?

A. 5
B. 8
C. 10
D. 15

(spoiler)

The answer is A. Among other formulas, the CLT provides you with $a^{2} + b^{2} = c^{2}$ for right triangles. (We recommend memorizing the reference formulas so you don’t have to spend time consulting them on test day!) In this formula, $a$ and $b$ are interchangeable, representing the two legs of the triangle. The most common mistake is to confuse one of the legs with the hypotenuse, plugging in the wrong value for $c$ . For this reason, it’s helpful to think of the formula in the other $c^{2} = a^{2} + b^{2}$ and make sure to identify c first. In this case, we know the value of $c$ : it’s 13. So we can write the formula either as $1 3^{2} = 1 2^{2} + b^{2}$ or $1 3^{2} = a^{2} + 1 2^{2}$ . Either way, solving for our variable will yield $5$ ( $169 - 144 = 25$ , which is $5^{2}$ ). We shouldn’t need to use answer elimination on this question, but if you used UnCLES method step of looking at the answers, you may have noticed that answer choice D is impossible because it makes one of the legs larger than the hypotenuse.

Note: $5 : 12 : 13$ is a Pythagorean triple, so if you have that memorized, you don’t need to use the Pythagorean theorem at all!

Triangle $A BC$ is similar to triangle $FG H$ , where angle A corresponds to angle $F$ . If the measure of angle $B$ is $48°$ and the measure of angle $H$ is $72°$ , what is the measure of angle $F$ ?

A. 48°
B. 60°
C. 72°
D. 90°

(spoiler)

The answer is B. Similar triangles have congruent corresponding angles, so when the question tells us that angle $A$ corresponds to angle $F$ , we know that those two angles are congruent. In addition, we may assume that the alphabetical order of the angles shows us the other corresponding pairs: $B$ and $G$ are congruent, as are $C$ and $H$ . That means that to discover the measure of angle $F$ , we could also calculate the measure of angle $A$ . The information given pertains to two different triangles, so we need to replace one of the angles with its corresponding partner from the other triangle. For example, if angle $B$ has a measure of $48°$ , then so does angle $G$ . Now that we have the measure of angles $G$ and $H$ , we can subtract their measure from $180°$ : $180 - 72 - 48 = 60$ .

Difficulty 2

A student is studying right triangles and comes up with the following conjecture:

If the lengths of a right triangle’s legs are integers, the length of its hypotenuse is an integer as well.

Which of the following is a counterexample that disproves the above statement?

A. A right triangle with leg lengths 3 and 4
B. A right triangle with leg lengths 7 and 8
C. A right triangle with leg lengths 8 and 15
D. A right triangle with leg lengths 9 and 12

(spoiler)

The answer is B. If you’ve completed the course module on logic, you have encountered counterexample questions, which ask you to disprove a statement by finding an exception to the rule proposed. In this case, we need to find the hypotenuse of each triangle presented in the answer choices; don’t forget about the helpful Pythagorean triples! The classic $3 : 4 : 5$ triangle eliminates choice $A$ right away; the hypotenuse is certainly an integer. If you remember that Pythagorean triples are ratios and that their multiples are also triples, you might notice that $9$ and $12$ (choice $D$ ) are multiples of $3$ and $4$ , respectively, and therefore that this another trio of integers.

From here, you have a clear path to the answer if you remember that $8 : 15 : 17$ is also a triple. That means answer $C$ is eliminated as containing three integers. If you didn’t remember that triple, it would be better to test answer $B$ since it has smaller numbers. Trying the Pythagorean theorem, we get $7^{2} + 8^{2} = c^{2}$ . If, therefore, $c = 113$ , we need to determine whether $113$ is a perfect square. Since $1 0^{2} = 100$ and $1 1^{2} = 121$ , it becomes evident that $113$ is not an integer, confirming choice $B$ as the answer.

An isosceles triangle has a base of $24$ inches and its other sides each equal to $13$ inches in length. What is the length of its height, in inches?

A. 5
B. 12
C. 13
D. 18

(spoiler)

The answer is A. As is typical, drawing is the first step! If the base of the figure is $24$ and the other two sides are congruent, we know from our Approach question to draw a vertical line down the middle of the triangle–especially since that’s exactly the length we’re trying to find in this case. That vertical line, or altitude, divides the isosceles triangle into two right triangles, and it divides the base evenly into $12$ and $12$ . That means each of our triangles has one leg of length $12$ and a hypotenuse of $13$ . You can use $a^{2} + b^{2} = c^{2}$ , but do you see the Pythagorean triple? It’s $5 : 12 : 13$ . $5$ is the missing height.

Difficulty 3

A triangle has lengths of $5$ , $12$ , and $14$ . Which of the following best describes this triangle?

A. It is a scalene right triangle.
B. It is a scalene non-right triangle.
C. It is an isosceles right triangle.
D. It is an isosceles non-right triangle.

(spoiler)

The answer is B. Examining the answers, we can eliminate choices $C$ and $D$ right away because an isosceles triangle has two equal sides and this triangle does not. This triangle is scalene, meaning that all of its side lengths are different. Is it a right triangle? We answer that question by plugging in the side lengths into the Pythagorean theorem to see if they satisfy the equation. $5^{2} + 1 2^{2} = 25 + 144 = 169$ . But $169$ is not the square of $14$ (the square of $14$ is $196$ ), so this is not a right triangle.

One more note: once again, knowing Pythagorean triples helps us answer more quickly. If you remember that $5 : 12 : 13$ is one of the Pythagorean triples, then those numbers constitute the lengths of a right triangle. Changing the largest number to 14 changes the hypotenuse, so we no longer have a right triangle.

A certain triangle has a $45°$ angle, a $90°$ angle, and two sides of length of $52$ . What is the perimeter of the triangle?

A. $102$
B. $152$
C. $102 + 10$
D. $152 + 15$

(spoiler)

The answer is C. This problem provides partial information that tells us everything we need to know to complete the triangle. First off, we know that the angle not mentioned must be $45°$ , because $180 - 90 - 45 - 45$ . So we have an isosceles triangle, also known as a $45 - 45 - 90$ . Consulting the CLT reference formula list, we see that the ratio of sides in a $45 - 45 - 90$ is $1 : 1 : 2$ .

What does this mean for the third side, whose length is not mentioned here? The clue is that we already know the length of two equal sides, so those must be the legs; the hypotenuse is missing. The tricky part is to apply the ratio to the known length of the legs in order to find the length of the hypotenuse. If we see that the two lengths of $52$ must correspond to the “1’s” in the ratio, then the hypotenuse must correspond to the $2$ . That means we need to multiply the leg length by $2$ to find the hypotenuse. What is $2$ times itself? Simply $2$ , because we are essentially squaring a square root, thereby canceling it. This means that $52 \times 2 = 5 \times 2 = 10$ . The hypotenuse is $10$ . We can now add that hypotenuse to the two legs and discover our perimeter of $102 + 10$ .

In case it helps you to see that ratio calculation done a different way, consider setting up a proportion as follows:

$1/5 2 = 2 / x$

In this proportion, the ratio parts ( $1$ and $2$ ) are in the numerator and the side lengths ( $52$ and x for the unknown hypotenuse) are in the denominator. Once we set up a proportion we should always cross-multiply; doing so gives us $x = (52) 2 = 10$ .

Difficulty 4

In trapezoid $A BC D$ below, $\overline{BC}$ is parallel to $\overline{A D}$ and $\overline{A B}$ is perpendicular to $\overline{BC}$ . What is the area of the trapezoid?

Note: the figure is not drawn to scale.

A. 60
B. 72
C. 84
D. 96

(spoiler)

The answer is D. Why this question in a lesson on triangles? Consider it a hint! If you get a non-standard figure on the CLT, such as this trapezoid, you should feel free to draw extra lines on the figure to divide it into more accessible parts. If we drop a vertical line from the top of the figure down to point $D$ , we’ll create a right triangle, as shown below.

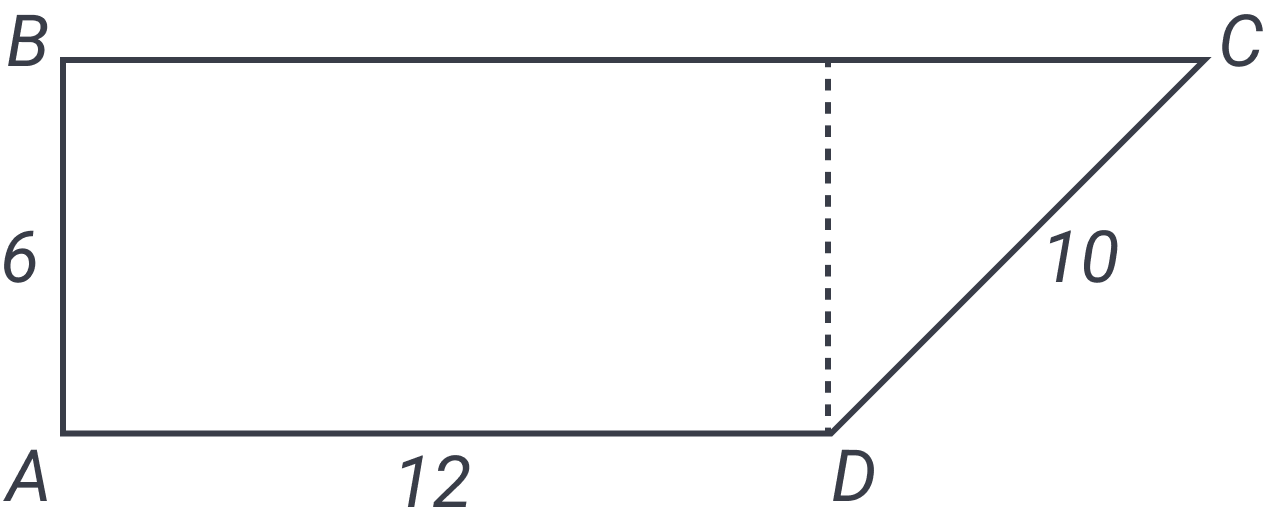
trapezoid ABCD with dashed line

We know the length of the dashed line is $6$ because it’s the same length as $A B$ . We now have a leg of length $6$ and a hypotenuse of length $10$ . Do you see the Pythagorean triple? It’s our old friend the $3 : 4 : 5$ , which means that the missing side is $8$ . After labeling that top portion of the triangle, notice that the rest of the upper side must be equal to side $A D$ , so we now know that the length of side $BC = 12 + 8 = 20$ . But even that isn’t strictly necessary; we can find the area of the trapezoid by adding the areas of its component parts, the rectangle and the triangle. The area of the rectangle is $6 x 12 = 72$ and the area of the triangle is $(½) (6) (8) = 24$ . $72 + 24 = 96$ .

The two-dimensional top of a paper airplane is represented by the figure below. A student wonders if triangles $A BC$ and $A C D$ are congruent. If it could be shown that $BC = C D$ , which of the following pieces of information would NOT be enough to provide that the two triangles are congruent?

A. $∠ B$ = $∠ D$
B. $∠ BC A = ∠ A C D$
C. $\overline{A B} = \overline{A D}$
D. Triangles $A BC$ and $A B D$ are similar triangles.

(spoiler)

The answer is A. In geometry, you probably learned about theorems side as $SSS$ (“side-side-side”) and $S A S$ (“side-angle-side”) that can be used to prove two triangles are congruent. Here are some reminders about that process:

Three congruent side pairs ( $SSS$ ) mean the triangles are congruent; three congruent angle pairs ( $AAA$ ) only prove that the triangles are similar.
If you have two congruent side pairs and one congruent angle pair, the angle pair must be the included angle between the two congruent sides in order to prove congruence. “Side-side-angle,” in that order, does not prove congruence.
Two congruent angle pairs and one congruent side pair always proves congruence; it doesn’t matter where the side is relative to the angles.

Given these principles, what can we conclude in this case? In the first place, this problem can’t be solved without noticing that we already have two congruent side pairs, not just one, because $A C$ is equal to itself and forms a side of both triangles. This means that we can prove congruence with either 1) a third side pair or 2) the included angle pair. Choice $C$ gives us the third side pair and choice $B$ shows us that the included angles (that is, the angles between the two sides we already know are part of congruent pairs) are indeed congruent. Both of those choices can be eliminated since we’re looking for the choice that is not sufficient.

Where from here? Think about what we learn from choice $D$ . If the triangles are similar, then all their corresponding angle pairs are congruent. So we have the angles we needed to prove congruence. Choice $A$ is the answer that does not prove congruence because it only supplies that insufficient “side-side-angle” relationship mentioned in principle #2 above.

Difficulty 5

A honeybee begins building a honeycomb with circular cells but the surface tension soon pulls the cells into a hexagonal shape. If each hexagon in the honeycomb has a side length of $3$ $mm$ , what is the area of each honeycomb? (Note: ignore the three-dimensional depth of the honeycomb.)

A. $63$ $m m^{2}$
B. $123$ $m m^{2}$
C. $13.5 3$ $m m^{2}$
D. $273$ $m m^{2}$

(spoiler)

The answer is C. Why is a hexagon question in this lesson? Because a regular hexagon divides nicely into six equilateral triangles, as shown in the figure below.

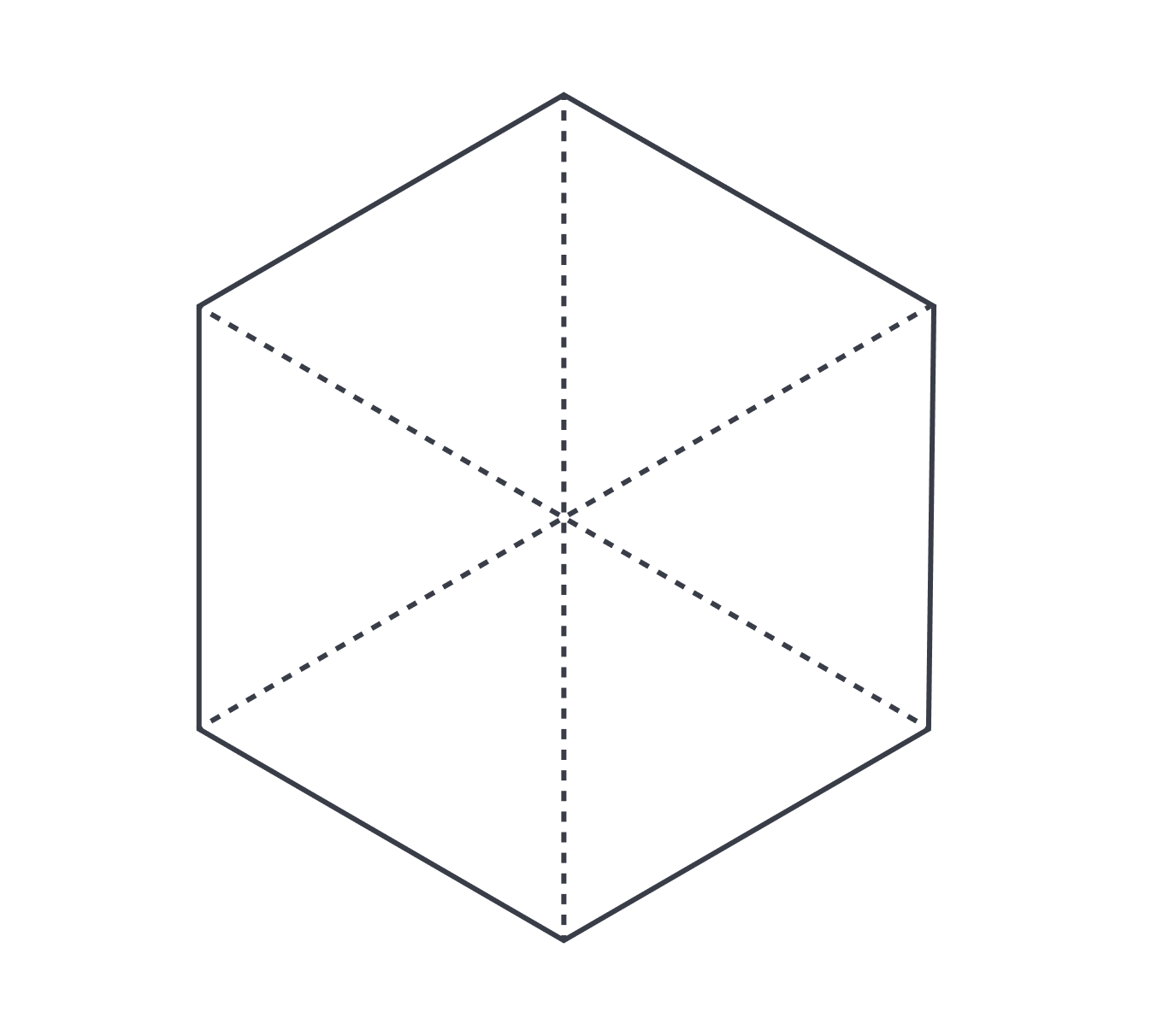
hexagon with six equilateral triangles

Each equilateral triangle has an area that can be discovered by dividing the triangle into two congruent $30 : 60 : 90$ right triangles. Pausing your reading for the moment, can you draw an equilateral triangle with sides of length and figure out its area using this method? It’s great practice in using a special right triangle such as a $30 : 60 : 90$ .

However, there is a faster way. The formula for the area of an equilateral triangle is $\frac{s ^{2} 3}{4}$ , where $s$ is the length of one side. Since these six triangles all have sides of length $3$ because they each share a side with the hexagon, we can plug three into the formula. That yields $(9/4) 3$ . But don’t forget that there are six of these triangles in the hexagon! Multiplying by $6$ and converting the fraction $54/4$ to decimal form yields answer $C$ .

By the way, unless the CLT specifically tells you to round or estimate, you should always leave the irrational numbers $π$ , $2$ , and $3$ as they are when making calculations. The answer choices will typically leave these values as they are as part of each answer. No one will ask you to make precise calculations of something like $3$ without a calculator!

Triangle $A$ is an isosceles triangle with two sides of length $3$ surrounding a $120°$ angle. Triangle $B$ is an equilateral triangle with sides of length $4$ . If:

P_A is the perimeter of triangle $A$ ,
A_Ais the area of triangle $A$ ,
P_Bis the perimeter of triangle $B$ , and
A_B is the area of triangle $B$ ,

which of the following lists the four quantities in order from least to greatest? (Disregard the “squareness” of the area units.)

A. P_A, A_B, A_A, P_B
B. A_A, P_A, A_B, P_B
C. P_B, A_A, P_A, A_B
D. A_A, A_B, P_A, P_B

(spoiler)

The answer is D. Jumping to Triangle $B$ , we can use the area of an equilateral triangle formula to find the area as $43$ . The perimeter is all the sides added together: $4 + 4 + 4 = 12$ . As mentioned in Flashcard Fodder, $2$ is approximately $1.4$ and $3$ is approximately $1.7$ . So the area of this triangle is approximately $5$ , which is much smaller than its perimeter. Using smart test strategy at this stage, we can eliminate any answer suggesting that the perimeter of Triangle $B$ is less than its area. That takes care of choice $C$ .

Triangle $A$ is not as straightforward. As with just about any isosceles triangle problem, it helps to draw the triangle with the equal sides diagonally on the right and left and draw a vertical line down the middle. In this case, the vertical line divides the triangles into two $30 - 60 - 90$ right triangles. Using those side ratios and discerning that the side of length $3$ would be the hypotenuse of each of these triangles, we can infer that the smallest side would $1.5$ and the middle side would be $1.5 3$ or $3/2 3$ . So the height of the isosceles triangle, being across from the $30°$ angle, is $1.5$ , and the base is both right triangle bases added together, or $33$ . That means its area is $2.25 3$ and its perimeter is $6 + 33$ . How do these numbers compare with the ones for Triangle B? $2.25 3$ is the smallest number we’ve found yet, as it’s clearly smaller than $43$ . This means that the area of triangle $A$ is the smallest value, so even just from that information, we can see that $D$ is the only possible answer. To confirm, we can note that the perimeter of triangle $A$ is about $11$ , just a little bit less than the perimeter of triangle $B$ . This also matches the list in answer choice $D$ .

This is a difficult problem, and if you have to make a guess, you might note that the side lengths for both triangles are fairly small, reasoning that, since the area formula for a triangle includes a $½$ , the areas of these triangles are likely going to smaller than the perimeters. (By contrast, if we imagine an equilateral triangle with sides of length $100$ , its area will be way larger than its perimeter.) That reasoning would lead you to the answer listing the areas as the two smallest quantities and the perimeter as the two largest quantities.

For Reflection

How will you approach triangles questions on test day? Write down at least three takeaways from this module.
Rate the difficulty of these ten questions for you from 1 (no problem) to 10 (problem!). This will help you decide when to answer them and when to skip them on test day.
There are a number of formulas and strategies in this lesson. Have you identified which ones you know and which you don’t? Make a plan to master the tools needed for triangles.