Right triangle trigonometry is one of the more consistent question types on the CLT; there is not a great degree of variation among these questions, and the acronym SOHCAHTOA is your relevant tool in virtually every case. Though word problems and logic problems can make the questions more complicated, the core skill of using SOHCAHTOA, plus a solid understanding of the tools for right triangles (Pythagorean triples, special right triangles, etc.) will equip you thoroughly for these questions.
Right triangle is similar to triangle . If , what is the value of ?
A.
B.
C.
D.
Draw, draw, draw! It is crucial to draw these figures so you can visualize them. (If, with practice, you find you see the figures in your head and answer more quickly, fine, but we heartily recommend you begin by drawing until you’re extremely comfortable). Your drawing of the two similar triangles should look something like this:
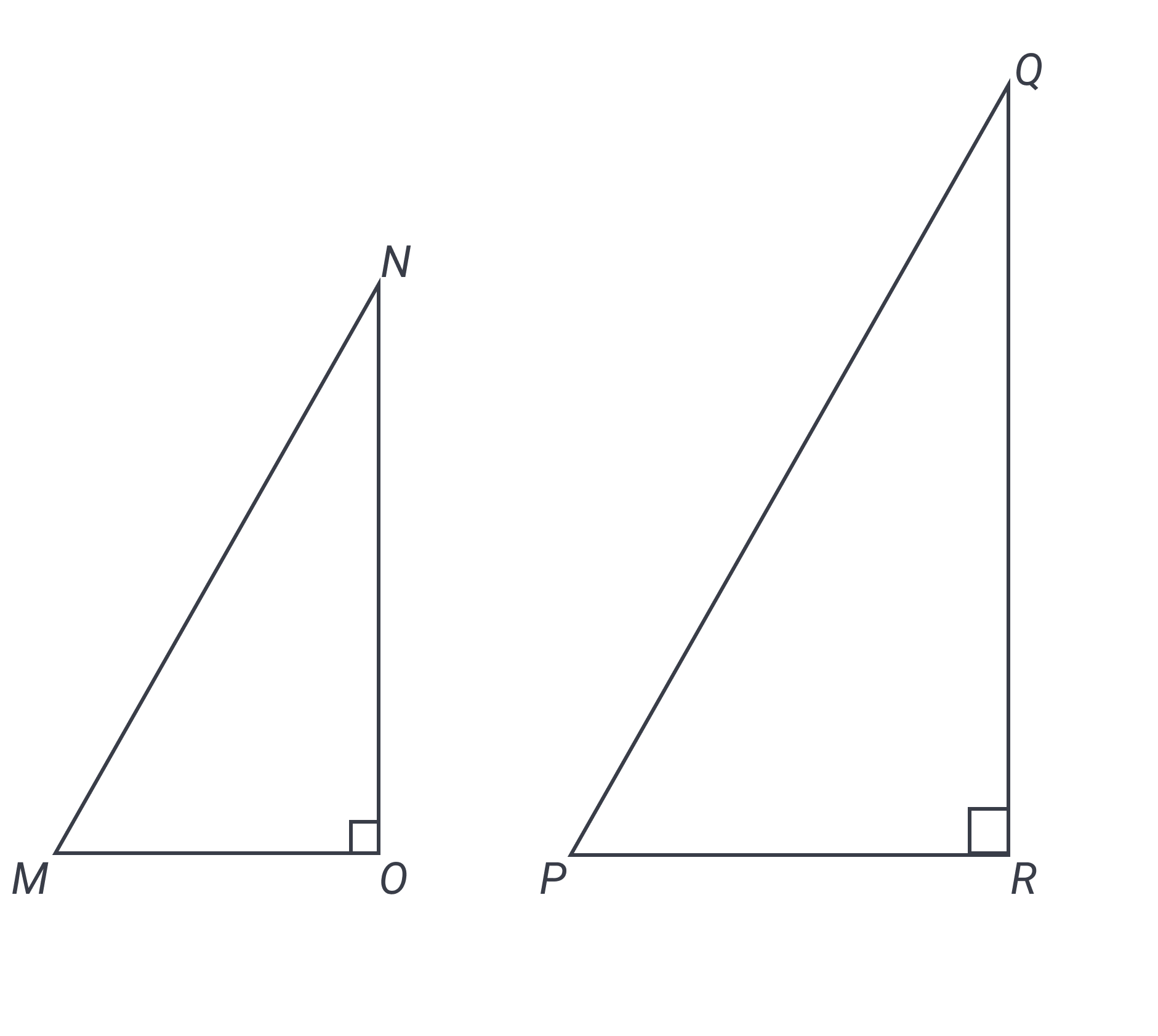
A couple of things to note about making this diagram: 1) we have made triangle larger than triangle , but it’s just as possible that it’s the other way around. The key is to recognize the triangles as similar and therefore having all the same angles and proportions. 2) We haven’t yet labeled the sides in triangle , and that’s by design. Using SOHCAHTOA to understand the tangent information, you could label side as and side as , but there’s a possibility of misleading yourself in that process.
Here is a crucial point, also noted in our Strategy Insights for this lesson: trig ratios from SOHCAHTOA are just that: ratios. They are not fixed values. Sides NO and MO might well be and , respectively, but they could just as well be and or and . It doesn’t matter; the only thing that matters is the ratio. And because similar triangles have identical proportions among their corresponding sides, we can transfer that ratio directly to triangle . In fact, it makes more sense to label this triangle with and so we can think about the third side (as long as we continue to keep in mind that this is a ratio). So let’s label side as and side as , in keeping with SOHCAHTOA. What does that mean for the hypotenuse? You can use the Pythagorean theorem, but it’s even better if you remember your triples: is a common right triangle ratio. In ratio terms, the hypotenuse must be .
We’re now to use SOHCAHTOA once again to get our final answer. Being careful to orient ourselves from angle , not angle , we look at adjacent, then hypotenuse, getting a ratio of . The answer is C.
One extra elimination note: choice is impossible because cosine can never be larger than (nor smaller than ). Looking for ways to eliminate answers can help you in making educated guesses!
It is theoretically possible that the CLT will include a right triangle trigonometry question that asks you to find one of the reciprocal trig ratios: cosecant, secant, or cotangent. Because those values are much more frequent in unit circle questions, we will introduce them in that lesson; if you understand what is presented in that lesson about these values, you will be able to apply that knowledge to a right triangle trig question should it become necessary.
Right triangle formulas provided by the CLT on test day
SOHCAHTOA, which means that:
The sine of an angle = ()
The cosine of an angle = ()
The tangent of an angle = ()
In right triangle , the length of side ; side ; and side . What is the value of ?
A.
B.
C.
D.
The answer is A. As always, draw the triangle. If you remember that the hypotenuse (longest side) of the triangle must be across from the right angle, that will help you draw the figure more quickly. Alternatively, you can note that side must be across from angle F, and “across” is precisely what we are seeking to find sine (opposite/hypotenuse). Whether you reason this way or use the diagram, the opposite is 14 and the hypotenuse must be . reduces to when you divide by two.
One final note: it’s always worth noting Pythagorean triples when they appear, and we have one here: is one of the less common triples, but a good one to know nevertheless!
In triangle , and . What is the value of ?
A.
B.
C.
D.
The answer is B. The key to this question is recognizing the special right triangle implied by the angles given. must be the right angle, so we know that is the smallest angle. This means (as shown in our lesson on triangles) that it must be across from the smallest side. As shown in the CLT reference list (though hopefully also solidly memorized by you!), the smallest side is represented by the in the ratio. This means that the ratio of the opposite in this case (smallest side) to the adjacent (middle side) is . Since opposite/adjacent is what we need for tangent, we are close to our answer.
What remains to be done? The rules of algebra tell us that a radical (in this case, a square root) in the denominator is not considered simplified, so we need to rationalize the denominator by multiplying both top and bottom of the fraction by that denominator. That gives us the following:
A right triangle has an area of square units. If the tangent of one angle of the triangle is , which of the following is the cosine of one of the angles of the triangle?
A.
B.
C.
D.
The answer is C. There are a couple of pieces of hidden, implied information here. We can’t yet use the area of because we don’t know the base or height of the triangle. However, the fact that the tangent of the triangle is is useful. This means that ; multiplying both sides by , we learn that . What does this tell us? We have an isosceles triangle, also known as a .
How do we move forward with this information toward the cosine of the triangle? The special right triangle in this case must have a ratio of , so that’s it! The cosine of that only one acute angle but both acute triangles must be (). As seen previously, we need to multiple both parts of the fraction by , and the result is choice .
Note that we didn’t ever use the area of the triangle! This is what’s known as extraneous (unnecessary) information in a problem, and identifying when you don’t need to use certain information can be important for efficient work on a standardized test like the CLT. However, just for the extra practice, can you use the area of this triangle to find out the lengths of its sides?
The sides are , , and . Because we know that the two legs here are congruent and that, in a right triangle, the length of the legs is equal to the base and height, we can use the area formula to posit that in this case. Solving for , we get , and the ratio tells us that the hypotenuse is the leg length of .
A student draws the following right triangle. Sin A = 8/17.
After performing some calculations, the student poses the following conjecture:
In a right triangle, the length of at least one of the legs is always less than half the length of the hypotenuse.
Which of the following right triangles provides a counterexample to the student’s conjecture?
A. A right triangle with a leg of length units and a hypotenuse of length units.
B. A right triangle where the sine of one angle = .
C. A right triangle where the cosine of one angle = .
D. A right triangle with one of length units and a hypotenuse of length units.
The answer is A. We might copy the figure and note the sine ratio here. However, since we (must!) note that trig ratios are only ratios, instead of labeling two sides and , let’s label them and to show that what we have is a ratio rather than fixed values. Do you remember the Pythagorean triple here? It is , so we can label the other leg .
The skill we just demonstrated can be helpful in many problems, so it’s worth considering, but in this case we don’t end up needing it. The ratio of shows us that we already have an example of what the student describes: is less than half of . We need to find an example of a right triangle where both legs have lengths more than half of that of the hypotenuse.
Jumping to the wrong answers first, we can note that choice actually poses the same triangle we already have: the triangle. So that choice doesn’t provide any extra information. Choice involves a common Pythagorean triple: . is certainly less than half of , so this answer does not provide a counterexample.
Choice might at first seem like the answer because is way more than half of , so perhaps the other leg of the triangle is also more than half of . But no such luck: the other side here, given by a lesser-known Pythagorean triangle, is . (If you don’t know that triple, you’ll have to do some Pythagorean theorem calculations with rather long numbers. is and is . , and the square root of is . You can see what a valuable shortcut a Pythagorean triple can provide!)
This leaves answer : a version of the classic triangle. Did you recognize it as a example? Since is and is , the remaining side must be . and are both more than half of , so this is our counterexample. If necessary, work on recognizing your triples, because if you don’t, you have to do an involved calculation with the Pythagorean theorem to find the third side of .
A student-athlete is standing at the edge of the roof of his school (warning: don’t try this at home!) and looking down at a football lying on the ground. If the angle of depression from the student’s eyes to the football is ° and the distance from the football to the base of the building immediately below the student’s eyes is feet, what is the distance from the student’s eyes to the football? (Note: assume that the building rises perpendicular to the ground and that the ground is level.)
A.
B.
C.
D.
The answer is B. If you didn’t already do so in attempting this problem, take a stab at drawing a picture of this situation. As true in so many other situations, visualizing it clearly is key. Now compare your figure to ours, below.
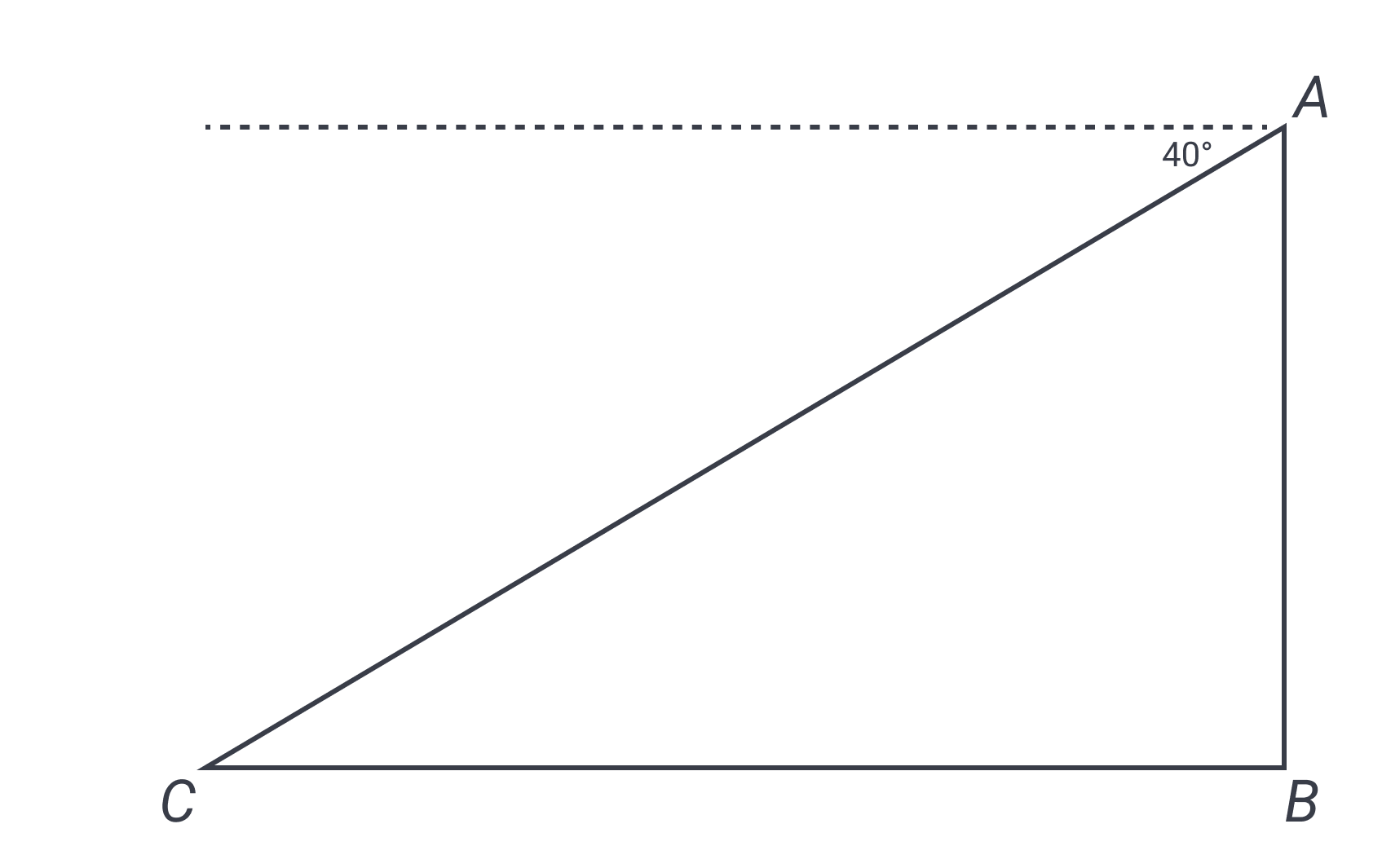
The angle of depression is the angle downward from a horizontal line drawn from the vantage point. As you can see from the diagram, the angle of depression is not one of the angles of our triangle, but because the building makes a right angle from the ground, we know we have a right triangle. This means the angle immediately below the angle of depression must measure because we also have a right angle between the building and the horizontal dashed line. (Alternatively, the horizontal line [shown dashed in our figure] must be parallel to the ground, we can use alternate interior angles to infer that the interior angle next to the football is ; therefore, the top angle of the triangle must measure .)
Labeling the bottom of the triangle because the given information in the triangle, we can now use trigonometry to find the distance requested, which is the hypotenuse of the triangle. Remember that the UnCLES guides us to look at the answers first; the angles listed in the answers show us that we need to distinguish between the angle at the top and the angle at the base. Which one should we use? The clue is that all the answers use sine. The length we know is the base of the triangle, and we know from SOHCAHTOA that sine deals with the opposite and the hypotenuse. We need use to the angle opposite the side whose length we know, so that must be the angle.
We can now set up the equation. Since , our equation is . Multiplying both sides by , we get . Remember that is just a number and must be kept together as one term. Dividing by , we get . Thankfully, the CLT leaves the answers in these terms; without a calculator, the value of would be hard to compute!
Considering the other answers, we already demonstrated why the choices with are incorrect. Choice would be the answer if had been the hypotenuse instead of the opposite side. Wrong answers to trig questions of this sort will often confuse multiplying and dividing in the way answer does compared to answer .
Sign up for free to take 5 quiz questions on this topic