Quadrilaterals and Polygons | Geometry

Introduction

Quadrilateral questions (questions about four-sided figures) on the CLT typically focus on rectangles (and squares, which are a type of rectangle), but they sometimes verge into other shapes like parallelograms and trapezoids. We will also cover questions about polygons with more than four sides, since they are fairly rare and are solved by dividing them into smaller shapes like triangles and quadrilaterals. You’ll see several word problems in the examples below, as the CLT frequently asks you to think about quadrilaterals in a real-life situation.

Approach Question

A park contains a rectangular swath of grass surrounded by a path uniformly $5$ feet in width. If the outer rim of the path has dimensions $80$ feet by $50$ feet, what is the area of the path, in square feet?

A. 400
B. 625
C. 1,000
D. 1,200

Explanation

This problem is an excellent example of why drawing diagrams on your scratch paper is so important; it’s very difficult to visualize the situation correctly without a diagram. Give it a try! Your diagram should look something like this:

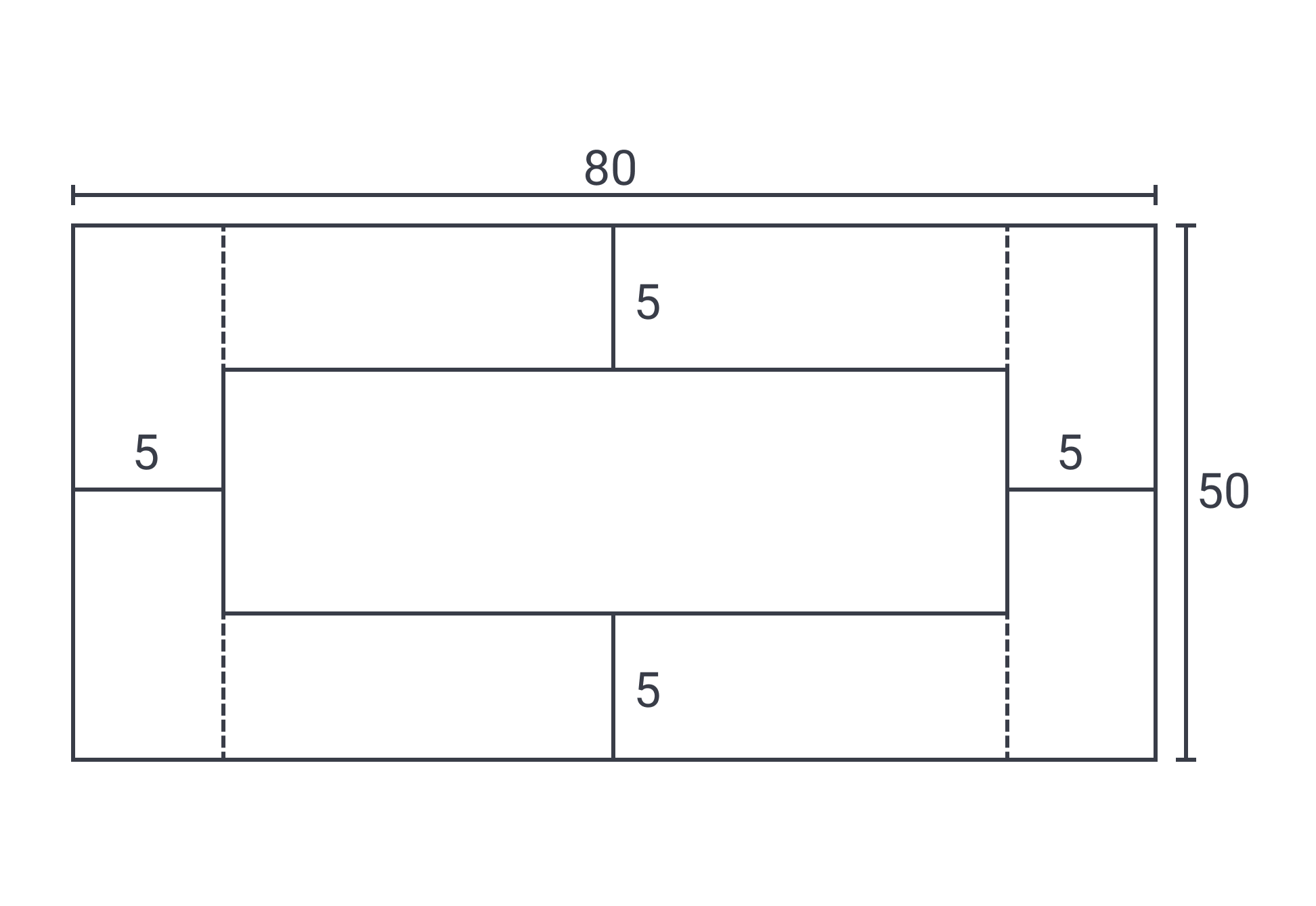
rectangular swath of grass surrounded by path

Note that the question describes an $80$ x $50$ setup on the outside of the path, not the inside (along the grass). This would be the first place where we could go wrong. Once we have those dimensions and the 5-foot-wide path clearly shown, we can approach the problem in one of two ways:

We can divide the path into four rectangles, as shown by the dotted lines in the diagram. The rectangles on the top and bottom of the bath have dimensions of $70$ x $5$ ; the rectangles on the sides, which included the entire 50-foot edge, have dimensions of $5$ x $5$ . We can find those areas by multiplying length times width in each case and adding the results together: $350 + 350 + 250 + 250 = 1200$ . The answer is D.
A somewhat simpler approach involves recognizing that many CLT problems involve finding an area by subtracting a smaller area from a larger area outside it. (This is often true in problems where a region of the diagram is shaded.) But be careful: to get the dimensions of the smaller rectangle, we have to subtract $10$ , not $5$ , from each dimension because the path is on both sides of the figure. Choice $B$ lurks if you make this mistake, but done correctly, the larger rectangle’s area is $50 \times 80 = 4000$ and the smaller rectangle’s area is $40 \times 70 = 2800$ . $4000 - 2800 = 1200$ .

Definitions

Polygon: A shape with three or more sides. Technically, you are likely to encounter mostly convex polygons, meaning that all of the sides of the polygon point away from its center. In a concave polygon, should you encounter it, one or more of the sides would point inward toward the center of the shape. This sort of polygon could still be divided into smaller shapes as described in Strategy Insights.
Similar: We covered this definition under triangles but are repeating it here to make sure you’re aware that similarity pertains to all polygons. We know two polygons are similar if all their corresponding angles are congruent (note that this means all rectangles are similar by definition because they always have only right angles). Once we know the polygons are similar, we can conclude that their corresponding sides are proportional. So, for example, if two rectangles have corresponding lengths of 6 and 8, their width must be the same basic 3:4 ratio to each other.
Parallelogram: A polygon with two parallel and congruent pairs of opposite sides. Subcategories of parallelogram include rectangle, rhombus, and square. Opposite angles in a parallelogram must be congruent; adjacent angles must be supplementary.
Rhombus: A parallelogram with all congruent sides. All of the properties of a parallelogram are true of the rhombus, with the addition that its diagonals are perpendicular.
Trapezoid: A quadrilateral with exactly one pair of parallel sides. Trapezoids on the CLT will usually, though not always, be isosceles; because these particular trapezoids have two congruent sides and their unequal sides are parallel to each other, they must have two pairs of congruent angles.

In addition to definitions, and since it’s helpful to see all the kinds of quadrilaterals and how they relate to each other, we are including the diagram below. We challenge you to recopy this for yourself and practice it until you can do it by memory!

types of quadrilaterals

Topics for Cross-Reference

Variations

The main alternative to a simple quadrilateral question is one that pairs a quadrilateral with another figure–usually a triangle or a circle. When a question has multiple figures, typically the first thing to identify is what those shapes have in common. For example, when a square is inscribed in a circle, the diagonal of the square is the same as the diameter of the circle.

Strategy Insights

Draw! Remember how the UnCLES method says, “If it’s a geometry problem, draw a figure.” In most cases, drawing the figure on your scratch paper will be crucial to understanding the problem thoroughly.
With polygons of more than four sides or with less common quadrilaterals, divide the figure into rectangles and triangles to help you understand the figure’s area. Remember how a regular hexagon divides nicely into six equilateral triangles; an octagon can be carved into a large rectangle and four triangles.

Flashcard Fodder

The most important formulas for quadrilaterals are for rectangles and squares:

Area of a rectangle = $l e n g t h$ x $w i d t h$ (this is in the CLT reference list)
Perimeter of a rectangle = $2 l$ + $2 w$
Area of a square = $s^{2}$ , where $s$ is the side length
Perimeter of a square = $4 s$

We’ll also repeat here the formulas regarding angles in a polygon.

Total degrees in the angles of a polygon: $(n - 2) (180)$ , where n is the number of sides
Degrees in each angle of a regular polygon: $\frac{( n - 2 ) ( 180 )}{n}$

Sample Questions

Difficulty 1

A student is planning a remodel of her bedroom including the purchase of a new desk. She wants the surface of the desk to take up no more than $10%$ of the room’s square footage. If the area of the room is $100$ square feet and the desks available are all $2.5$ feet wide, how long, at most, can the student’s desk be? (Ignore the height of the desk in making your calculation.)

A. 3 feet
B. 4 feet
C. 5 feet
D. 6 feet

(spoiler)

The answer is B. Sometimes CLT geometry problems will include a percentage or a fraction when considering comparisons in area. Fortunately, the total square footage is an even $100$ here so the maximum surface area of the desk is a clean $10$ square feet ( $10%$ of $100$ ). If the desks are $2.5$ feet wide, then we need to divide $10$ by $2.5$ , because $2.5 l = 10$ ( $a re a$ = $l e n g t h$ x $w i d t h$ ). The desk can be up to $4$ feet long.

Difficulty 2

Rectangle $A BC D$ is similar to rectangle $MNOP$ . If the area of $A BC D$ is $60$ square units and $MNOP$ has a width of $4$ , which of the following must be true?

A. Both rectangles are squares.
B. Rectangle MNOP has a length of 12.
C. Side AB is perpendicular to side BC.
D. Rectangle ABCD has a length of 15.

(spoiler)

The answer is C. This problem is tricky in that can be tempting to think we know more than we actually do. We have the width of one rectangle but we don’t have a corresponding width for the other rectangle; we have an area of one triangle but no corresponding area of the other. This means that we should stay away from answers like choices $B$ and $D$ ; there’s no way to find any of the unknown widths, lengths, or areas. Choice $A$ would be an eternal truism if it read the other way; all squares are rectangles, but since not all rectangles are squares, we don’t know if choice A is true.

The right answer is something that, surprisingly, we would have known all along without any information except that the two polygons are both rectangles. Since rectangles have all 90° angles, any two of their adjacent sides must be perpendicular. Side $A B$ must be adjacent (connecting) to $BC$ because they both contain $B$ , which marks a vertex of the rectangle.

Difficulty 3

The area of a rectangle is given by $6 x^{2} + 2 x$ . If one of the sides measures $3 x + 1$ , find the perimeter of the rectangle.

A. $10 x + 2$
B. $5 x + 1$
C. $3 x^{2} + 1$
D. $2 x^{2}$

(spoiler)

The answer is A. As with many other problems, we should draw the rectangle here, labeling one of the sides $3 x + 1$ . (It doesn’t matter which side we choose; although it is traditional to make a rectangle’s length longer than its width, standardized tests don’t typically make this distinction. Also, since we’re just trying to come up with $2 l + 2 w$ , the perimeter of the rectangle, it won’t matter which side we call $l$ and which side we call $w$ .)

We can use the rectangle area to understand that $3 x + 1$ times something must equal $6 x^{2} + 2 x$ . What is that something? Do you see the $3 : 1$ ratio between the terms of both binomials? This suggests that we might want to factor out something from $6 x^{2} + 2 x$ ; the greatest common factor of that binomial is $2 x$ . If we factor out $2 x$ we get, you guessed it, $3 x + 1$ . So we now know the two dimensions: $2 x$ by $3 x + 1$ . Adding them together and doubling the result (don’t forget to double for the perimeter! If you forget, you’ll get answer $B$ ) gives us $10 x + 2$ .

Difficulty 4

A student is thinking about parallelograms and comes up with the following conjecture:

The diagonals of a parallelogram are always perpendicular.

Which of the following is a counterexample that disproves the above statement?

A. A parallelogram in which all sides are $6$ units long.
B. A parallelogram whose diagonals create four right triangles.
C. A parallelogram with interior angles that are all $90°$ .
D. A parallelogram with two sides of length $5$ units and two sides of length $9$ units.

(spoiler)

The answer is D. You may remember, if you really excelled in geometry in school, that there’s a certain kind of parallelogram whose diagonals are perpendicular. (If you remember that, we’re impressed!) Let’s assume you don’t remember that property exactly and use some diagramming to support your thinking. First, picture a long, skinny parallelogram like the one in the figure below. (Is it us, or are we basically drawing the state of Tennessee?) Next to it, draw a parallelogram that is more squat, so that it appears its sides might be somewhere close to congruent (hint hint).

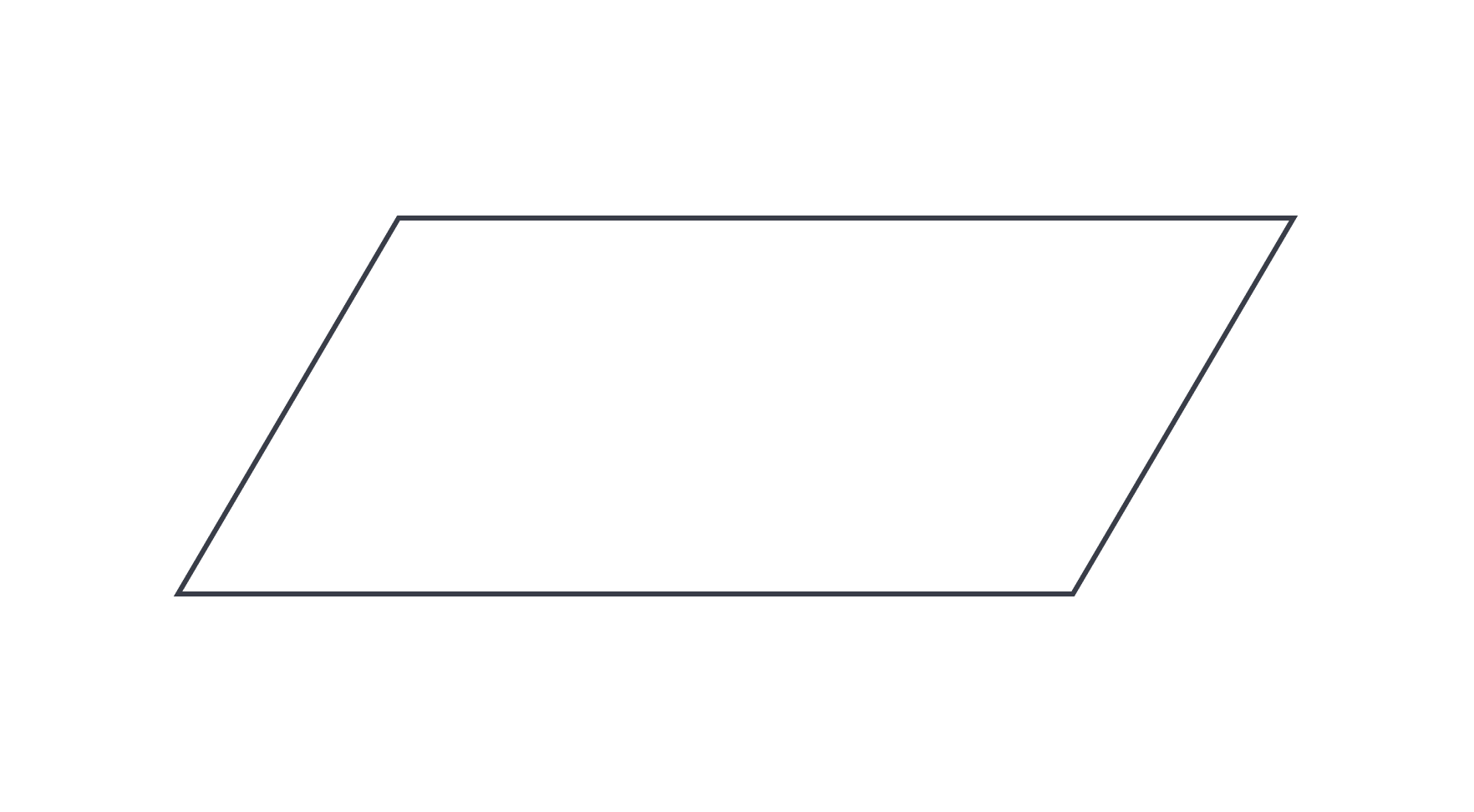
long, skinny trapezoid

rhombus all sides congruent

Now draw the two diagonals of both parallelograms. You may notice that the diagonals in the long, skinny parallelogram don’t seem to be anywhere close to perpendicular, but the diagonals of the other parallelogram could be. This moves us closer to the truth about perpendicular diagonals, that among parallelograms, only the rhombus (all sides congruent) has perpendicular diagonals.

With this in mind, we can eliminate answer choice A because it agrees with the student’s statement rather than violating it. Reading choice $B$ carefully shows us that it’s saying something identical to the student’s conjecture; perpendicular lines, by definition, create right angles. Choice $C$ is trickier because it brings up $90°$ , but we’re looking for $90°$ angles at the intersection of the diagonals, not at the vertices. What choice $C$ is telling us is that we have a rectangle. But the question is, is that rectangle a square? A non-square rectangle would be a nice counterexample here, but since we can’t rule out a square, and a square is a type of rhombus, choice $C$ leaves us uncertain. Choice $D$ is clearer because it resembles our first parallelogram: the long, skinny one. Understanding now that the student is talking only about parallelograms that are also rhombuses, we can safely choose answer $D$ as the counterexample.

Difficulty 5

A stop sign (octagonal in shape) has two identical horizontal, parallel scratches in it that stretch from one diagonal to another and divide the octagon into a central rectangle and two isosceles trapezoids above and below the rectangle. If each side of the stop sign has a length of $6$ inches, what is the combined surface area of the two trapezoids created by the parallel scratches?

A. $182$
B. $18 + 182$
C. $362$
D. $36 + 362$

(spoiler)

The answer is D. This is another figure we should draw so that we can see clearly what’s happening. The question asks us to focus just on the trapezoids, so we can ignore the rectangle unless that helps us with the trapezoid. It looks like the only thing we know about each trapezoid is all the slant heights are 6 inches long because they are identical to the sides of the octagon. We would do well to divide each trapezoid into a central rectangle with triangles on the end, like so:

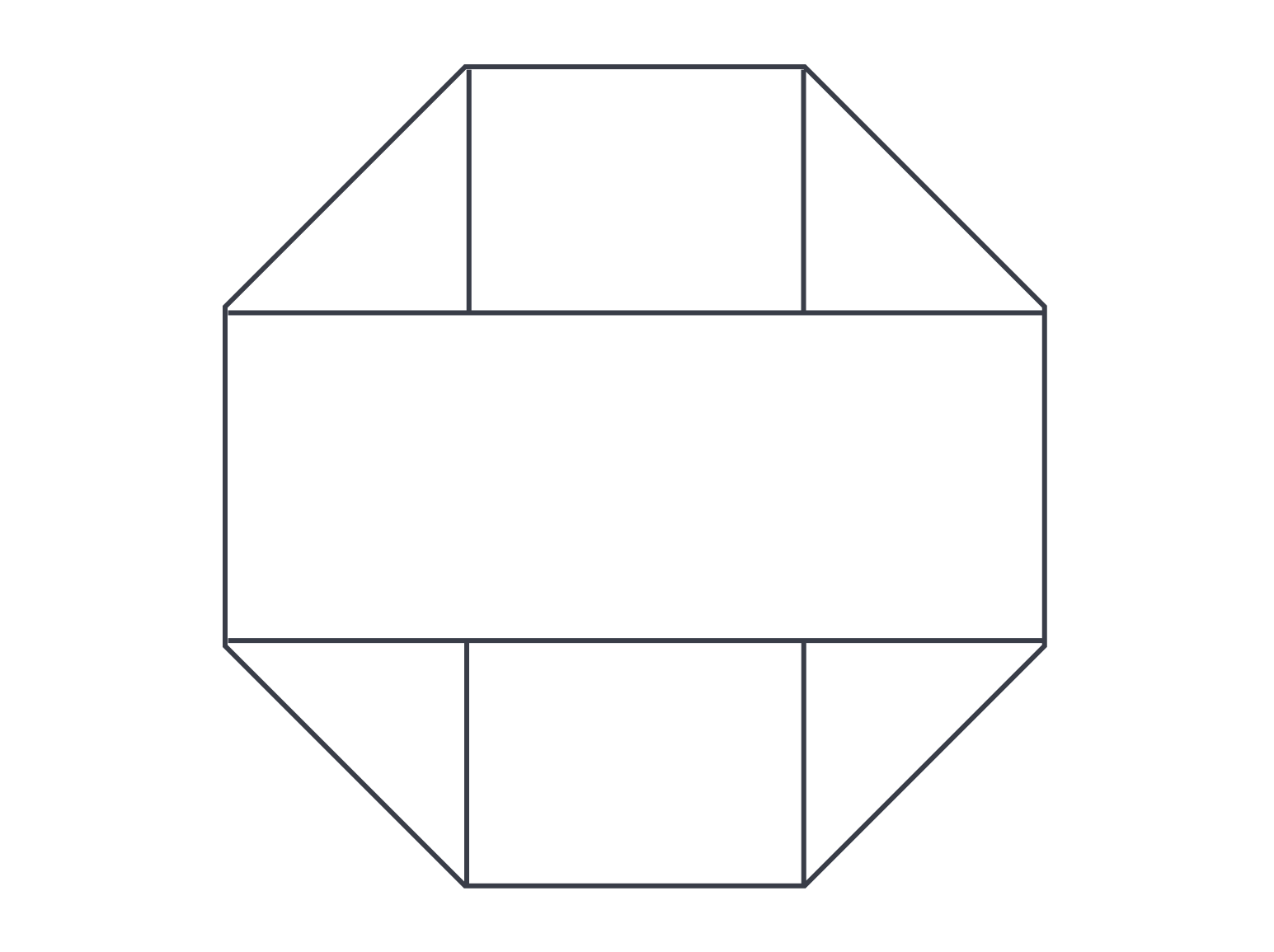
octagon with rectangle and two isosceles trapezoids

These triangles appear to be isosceles right triangles ( $45 - 45 - 90$ ), and indeed they are. The proof of that fact has to do with the fact that octagons have $135°$ interior angles, which in this case divide into $90°$ and $45°$ . But even if you are uncertain of that, it makes sense on standardized tests to assume that shapes appearing in familiar ways are in fact familiar (for example, if it looks like a right angle, it probably is!). Since the hypotenuse of these little triangles is $6$ , we work backward to the legs using the $45 - 45 - 90$ relationship and discover that the legs are $\frac{6}{2}$ in length. So the area of each of the triangles is $(\frac{1}{2}) (\frac{6}{2}) \frac{6}{2} = 9$ . $\frac{6}{2}$ also becomes a side of the rectangle, while the other side is $6$ because it mirrors the side of the octagon. So each of the two rectangles has an area of $(6) (\frac{6}{2}) = \frac{36}{2}$ . Multiplying that area by two because there are two rectangles (one inside each trapezoid) and multiplying the triangle area by $4$ to account for all the triangles, then adding it all together, we come to $36 + \frac{72}{2}$ .

That result doesn’t match any of the answer choices. What went wrong? Nothing, as it turns out; we have to remember that, according to the rules of algebra, a radical (in this case a square root) in the denominator means the fraction can be further simplified. So we must transform the second term in our answer. We rationalize the denominator by multiplying both top and bottom by $2$ . This results in $2$ in the denominator, which divides evenly into the numerator of $722$ . The result is $36 + 362$ , answer choice $D$ .

For Reflection

How will you approach quadrilateral and polygon questions on test day? Write down at least three takeaways from this module.
Rate the difficulty of these questions for you from 1 (no problem) to 5 (problem!). This will help you decide when to answer them and when to skip them on test day.
Can you name all the major types of quadrilaterals and explain how they relate to each other? For example, all squares are rectangles but not all rectangles are squares.