Introduction

Circle questions rely heavily on the two core circle formulas (circumference and area), often dealing with both together in the same problem. Like quadrilateral problems, circle problems of higher difficulty overlap circles with other shapes–usually quadrilaterals but also sometimes triangles as well. As with triangles, knowing your formulas is crucial, especially as there are several formulas, equations, and properties for circles that are not included in the CLT reference list.

Approach Question

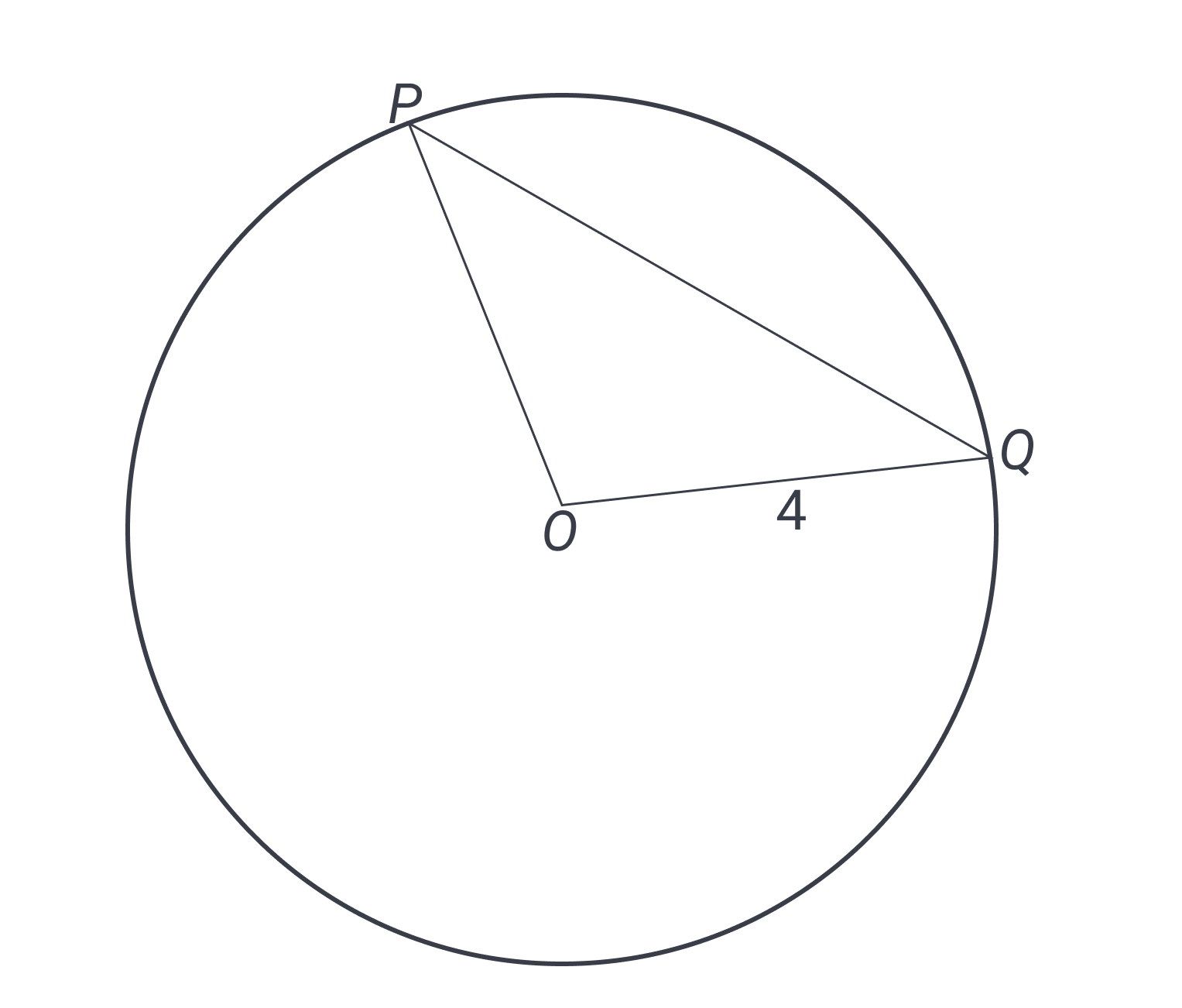
In the circle below, $O$ is the center and $OPQ$ is a triangle with points $P$ and $Q$ on the circle. If the measure of angle $OPQ = 30°$ , what is the length of arc $PQ$ ?

circle with triangle OPQ within

A. $16 π$
B. $8 π$
C. $\frac{8}{3} π$
D. $\frac{4}{3} π$

Explanation

This question is typical of many CLT circle questions in that it includes another shape along with the circle. An important principle whenever you encounter overlapping shapes is to determine what the two shapes have in common. In this case, we must note that line segments $OP$ and $OQ$ are both sides of the triangle and radii of the circle. As always with CLT geometry, let’s copy the figure so we can annotate it.

That realization unlocks a key recognition: this is an isosceles triangle because all radii of a circle must be the same length. On your copied figure, add the given information about angle $OPQ$ measuring $30°$ . Since this is an isosceles triangle, another angle must also measure $30°$ ; we know that must be angle $PQO$ , both by appearances and because that is the other angle across from one of the two congruent sides. Using the knowledge that a triangle’s angles sum to $180°$ , we can deduce that angle $POQ$ , the central angle, is $120°$ .

Here is where an important circle property comes in: the degree measure of the central angle is equal to the degree measure of the arc that it intercepts. So if angle $POQ$ is $120°$ , then the measure of arc $PQ$ must also be $120°$ .

At this juncture, we should pause to include the reminder that arcs, which are portions of a circle’s circumference, can be represented in two different ways. They can be measured by degrees, where $360°$ is all the way around the circle, and they can also be measured as a fraction of a circle’s circumference. This latter measure is known as the arc length and will typically include $π$ because it represents a portion of the circumference, for which the formula is $2 π r$ .

This definition of arc length helps us understand that the question is asking for a portion of the circumference. Since we have a radius labeled as $4$ , we know from the formula that the circumference of our circle is $8 π$ . But what portion of the circle does arc $PQ$ occupy? Since we know the arc’s measure is $120°$ , we can divide that measure by $360$ to get the relevant fraction. $\frac{120}{360}$ reduces to $\frac{1}{3}$ ; we have $\frac{1}{3}$ of the circle encompassed by arc $PQ$ . Since $\frac{1}{3}$ of $8 π$ is $\frac{8}{3} π$ , the answer is C.

Definitions

Chord: A line segment connecting any two points on a circle. A diameter is an example of a chord, but not all chords are diameters. Any chord that is not a diameter must, by definition, be shorter than the diameter.
Radius: The distance from the center of a circle to any point on the circle. All radii are equivalent in length to each other, which we can see from the textbook definition of a circle the set of all points equidistant from one point. The “one point” in this definition is the circle’s center.
Diameter: A line segment connecting two points on a circle and passing through the center. More informally, a diameter is the distance across a circle. Another way to describe a diameter is that it’s the longest chord that can be drawn in a circle.
Circumference: The distance around a circle, given by the formula $2 π \times r a d i u s$ .
Arc: A portion of the circumference of a circle. Since the circumference is the distance around a circle, an arc must be drawn along the outside of a circle.
Sector: A portion of the area of a circle. If you envision a pizza divided into slices, each slice would represent a sector. The same can be said of a pie chart.
Inscribed: Drawn inside another figure with all possible edges touching. If a square is inscribed in a circle, the square’s four vertices are on the circle; if a circle is inscribed in a square, four points on the circle touch the square at the middle of each side of the square.
Circumscribed: Drawn around another figure with all possible edges touching. The opposite of “inscribed”.

Topics for Cross-Reference

Variations

This lesson’s problems with multiple figures illustrate how circles are presented alongside polygons. Circles will also occasionally appear in problems with three-dimensional solids–for example, a cross-section of a sphere is a circle, as is a cross-section of a cylinder if it is cut parallel to the circular bases.

Strategy Insights

This is a reminder from previous geometry modules: be ready to draw the figure on your scratch paper, especially if a figure is not provided with the question.
When two figures overlap, such as a square inscribed in a circle, consider what the figures have in common. There will typically be some line segment that constitutes an important part of both figures, and that similarity will unlock the problem.
With circles as well as quadrilaterals, the principle of dimensions becomes all-important in certain questions. Imagine that the room you’re sitting in (assuming that room is a rectangle) has both its length and its width doubled. What has happened to the area of that room’s floor? The area is not double; it’s quadrupled because both the length and width are doubled. So it follows that if you double the length of a square’s sides, you quadruple the area of the square. For a circle, we get a hint that the same principle applies in the fact that the area formula has a squared term. If we, say, triple the radius of a circle, the area is multiplied by a factor of nine. Whatever action we do to the radius, we have to square the effect of that action on the circle. So, to name a corollary by example, if we discover that a circle’s area has increased by a factor of $25$ , we can deduce that the radius of that circle has been increased by only a factor of $5$ .

Flashcard Fodder

Circle formulas provided by the CLT on test day:

Area of a circle = $π r^{2}$

Circumference of a circle = $2 π r$

Degrees in a circle = $360$

Circle formulas NOT provided by the CLT on test day:

The equation of a circle: $(x - h)^{2} + (y - k)^{2} = r^{2}$ ; ( $h$ , $k$ ) is the center of the circle and $r$ is the radius.

The arc length formula $(n /360) (2 π r)$ , where n is the degree measure of the arc

The sector area formula $(n /360) (π r^{2})$ , where n is the degree measure of the central angle

Two important right angle properties concerning circles:

A line tangent to a circle forms a right angle with the radius of the circle at the place where the two lines meet.
The hypotenuse of a right triangle inscribed in a circle or semicircle is always identical to the diameter of the circle (or semicircle).

Sample Questions

Difficulty 1

A circle has an area of $64 π$ units squared. What is its circumference?

A. $64$ units
B. $8 π$ units
C. $16 π$ units
D. $64 π$ units

(spoiler)

The answer is C. Among other formulas, the CLT provides you with the circumference formula of $2 π r$ and the area formula of $π r^{2}$ . We need to use both in this case. First, we set the circumference formula equal to $64 π$ : $π r^{2} = 64 π$ . Cancel the $π$ on both sides and we get $r^{2} = 64$ , so $r = 8$ .

We now plug the radius of $8$ into the circumference formula: $2 \times 8 \times π = 16 π$ . Note that the CLT will virtually always leave $π$ in the answer choices. They know you don’t have a calculator and don’t expect you to calculate $π$ !

Difficulty 2

A circle has an area equal to its circumference (disregard the “squareness” of the area). What is the radius of the circle?

A. 1 unit
B. 2 units
C. 4 units
D. 8 units

(spoiler)

The answer is B. To understand how the circle’s area could be equal to its circumference, we set the two formulas equal to each other in an equation: $π r^{2} = 2 π r$ . After canceling the $π$ on both sides, we have $r^{2} = 2 r$ . Although we might be tempted to take the square root of both sides, that’s not algebraically helpful because it will put the term $2 r$ under a square root.

Instead, we’ll follow our principle for quadratics (anything with a variable raised to the second as the highest power in the expression): set quadratic equations equal to zero. Doing so and factoring yields the following:

$r^{2} - 2 r = 0 r (r - 2) = 0 r = 0 OR r = 2$

Since it’s nonsensical to have a radius of zero units, the answer must be $2$ .

Difficulty 3

Circle $A$ has four times the area of Circle $B$ . If the radius of Circle $B$ is $5$ cm, what is the radius of Circle $A$ ?

A. 10 cm
B. 15 cm
C. 20 cm
D. 25 cm

(spoiler)

The answer is A. The principle of dimensions is so important that we include it in detail in the Strategy Insights for this lesson. Put briefly, because a radius is a one-dimensional concept but area is a two-dimensional concept, they are not affected in the same way. We can discover this by actually calculating the area of circle $B$ : $π \times 5^{2} = 25 π$ . Circle $A$ , we are told, has an area four times that large, so the area of Circle $A$ must be $100 π$ . What, then, is the radius of Circle $A$ ? It must be the square of $100$ , which is $10$ .

Note the trap answer here! Choice $C$ is very tempting because $20$ is four times as much as $5$ . But the principle of dimensions tells us that’s a trap answer; it will always be a trap answer in questions like this.

Difficulty 4

A square with an area of $9$ inches is inscribed in a circle. What is the area of the circle?

A. $\frac{3}{4} π$
B. $\frac{3}{2} π$
C. $\frac{9}{4} π$
D. $\frac{9}{2} π$

(spoiler)

The answer is D. We find here another example of a circle interacting with another shape, so we follow the strategy of determining what line segment the two shapes have in common. A square inscribed in a circle looks like this:

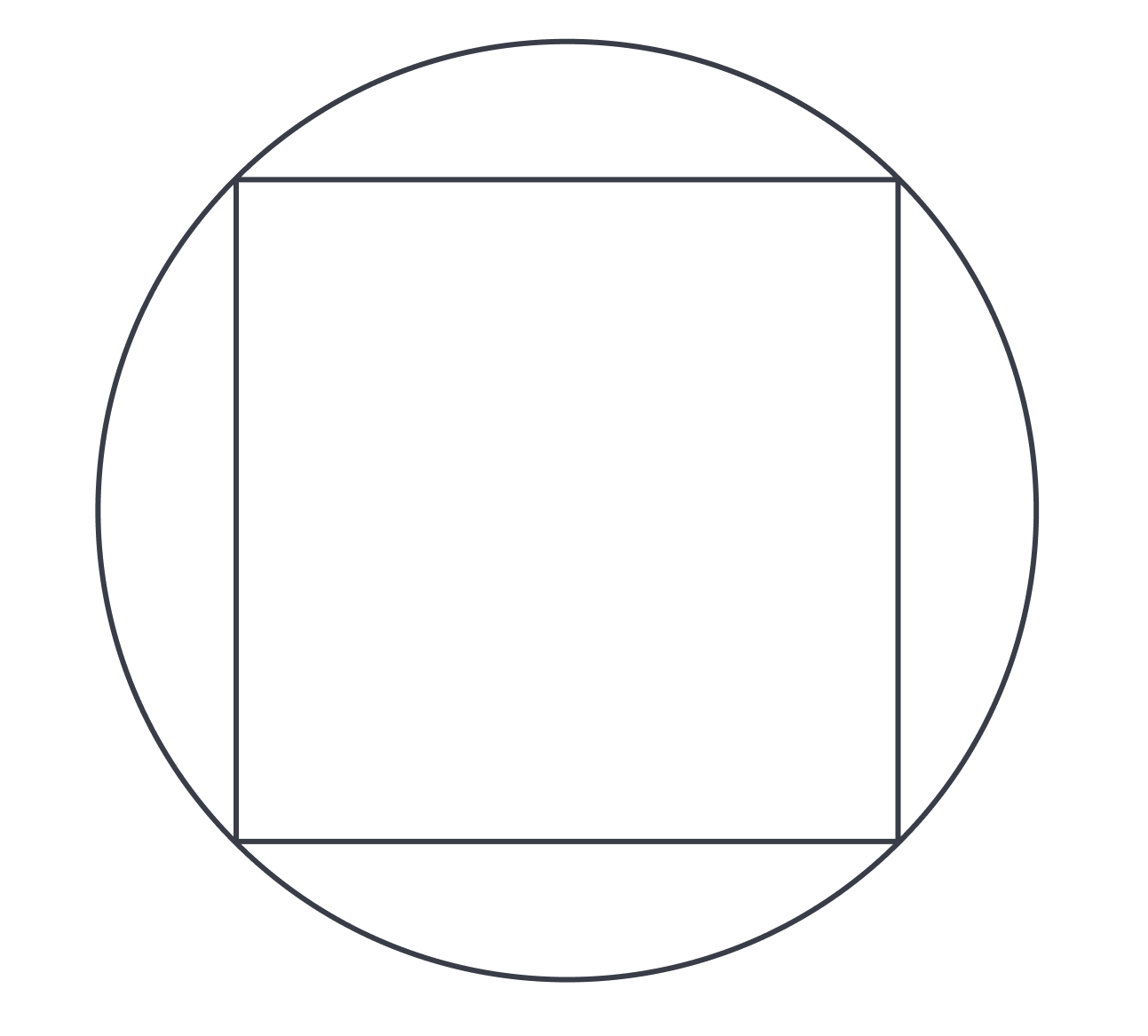
circle with square inscribed

From this picture alone we don’t have a significant line segment in common. (We could say that each side of the square is a chord of the circle–that is, a line segment connecting two points on the circle–but there are no formulas regarding chords that the CLT is likely to use.) However, what about connecting two of the opposite vertices (corners) of the square? If we do that, we’ll have a diameter of the circle, as shown below:

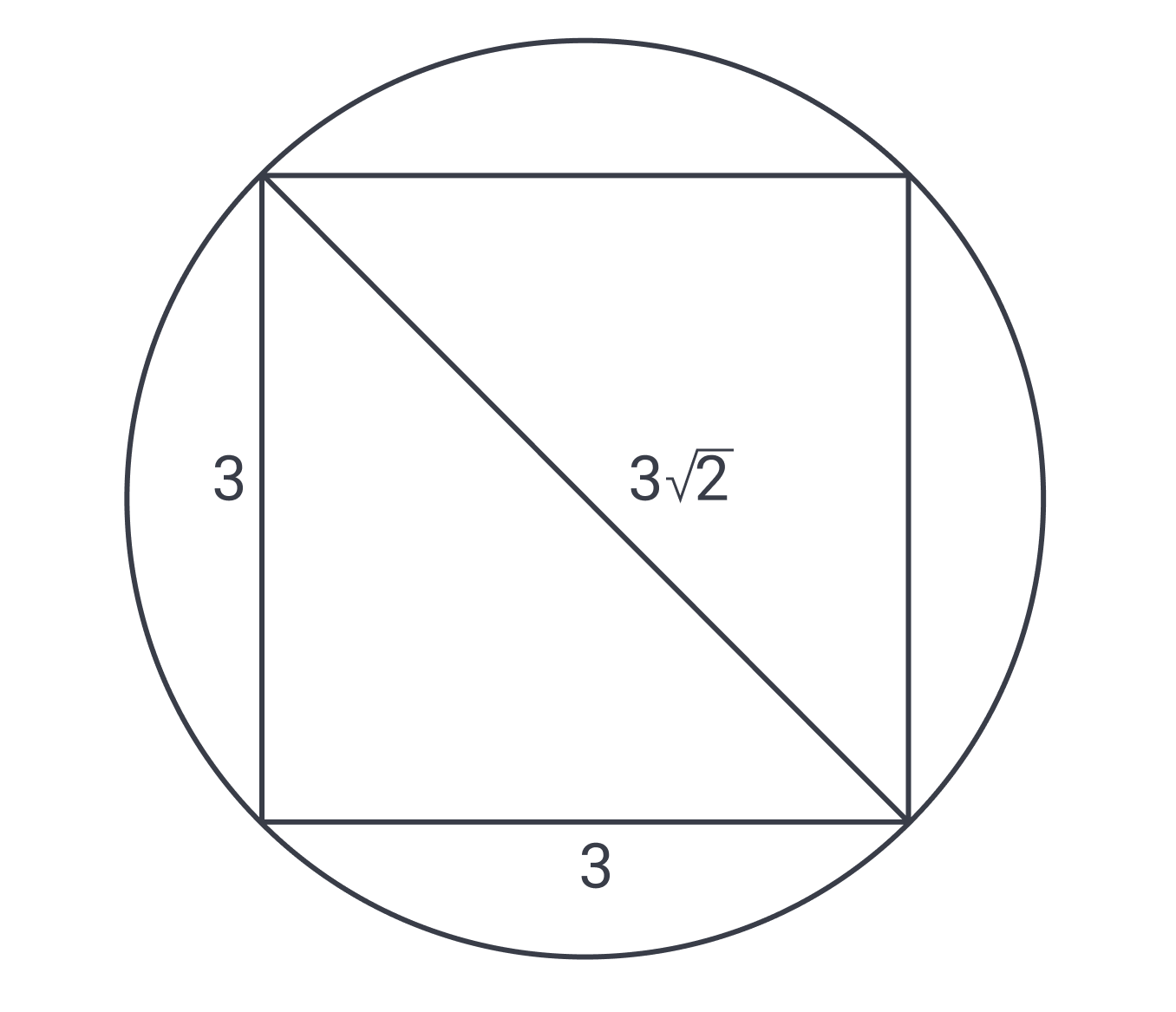
circle with square inscribed with connecting two of the opposite vertices

So, the diagonal of the square is identical to the diameter of the circle; there’s a line segment in common! The figure also shows the sides of the square as $3$ , which must be true since the area of the square is $9$ . Finally, if you studied well using our unit on triangles, you’ll recall that an isosceles triangle like this one is a $45 - 45 - 90$ special right triangle, so the hypotenuse is equal to the length of a leg times $2$ . The figure shows this result as well.

Our remaining task is to calculate the area, but since we only have the diameter, we must calculate the radius first. Radius length is $\frac{1}{2}$ of diameter length, so this radius must be $\frac{3}{2} 2$ . Squaring that quantity involves squaring both parts, giving us $\frac{9}{4} (2)$ , which equals $\frac{18}{4}$ or, simplified, $\frac{9}{2}$ .

A circular fence encloses a school’s baseball field. A portion of the fence equal to a $50°$ arc is painted with the school’s colors; the rest is left unpainted. If the longest distance across the field from fence to fence is $360$ feet, what is the length of the portion of the fence not painted, in feet? (Note: ignore the height of the fence.)

A. $50 π$
B. $100 π$
C. $260 π$
D. $310 π$

(spoiler)

The answer is D. As usual, you should draw the figure on your scratch paper to envision the situation. The UnCLES method reminds us to observe right away what the question is asking for; the fact that we are looking for the part not painted helps our strategy right away. If the painted portion is equal to $50°$ , then the unpainted part must be equal to $360 - 50 = 310°$ .

We can use the arc length formula once we have the radius. If the distance across the field is $360$ , then the radius must be $180$ . Plugging $180$ and $310$ in the formula looks like this:

$\frac{310}{360} \frac{31}{36} (31) (31) (2 \times π \times 180) (360 π) (\frac{360 π}{36}) (10 π) 310 π$

Note how we rearranged the factors to divide $360$ by $36$ , since that results in the integer value $10$ . Working these problems without a calculator and with limited time requires that you seek ways to streamline the process. Also, although you can certainly memorize the arc and sector formulas, it also helps to realize that they both involve using the arc measure to find the fraction of the circle you’re dealing with. The only difference from there is that arc length is that fraction times the circumference while sector area is that fraction times the area.

Difficulty 5

A line is tangent to a circle at the point $(3, 7)$ ; the circle’s equation is $x^{2} + y^{2} - 6 y = 16$ . What is the slope of the tangent line?

A. $- \frac{4}{3}$
B. $- \frac{3}{4}$
C. $\frac{3}{4}$
D. $\frac{4}{3}$

(spoiler)

The answer is B. This is a complicated question that invokes 1) the skill of completing the square; 2) the circle equation $[(x - h)^{2} + (y - k)^{2} = r^{2}]$ ; and 3) the fact that a tangent line is perpendicular to the radius at the point where the two lines intersect.

We begin by seeking to interpret the circle based on the circle equation, but notably the equation is not yet in the proper form. This is where completing the square comes in. We’ll begin with the y terms and return to x later. We can copy down $y^{2} - 6 y$ , but we’re used to seeing a third term in this expression in order to factor it. What is that third term? We know from the form of the circle equation that we are looking for a perfect square quadratic, something that will factor into the form $(y - k)^{2}$ . Completing the square involves two steps:

Divide the coefficient of the first-degree term (the term raised to the first power) in half;
Square the result.

The coefficient in this case is $6$ , so by dividing it in half and squaring it, we get $9$ . We add the $9$ after our first two terms to make $y^{2} - 6 y + 9$ . But we can’t just change an equation; that would unbalance it! So we add $9$ to the other side as well, making $25$ . $y^{2} - 6 y + 9$ can be factored into $(y - 3) (y - 3)$ or, better, $(y - 3)^{2}$ . That gives us the desired form $(y - k)^{2}$ . Since that process is challenging to remember and repeat, here it is again, line by line:

$x^{2} + (y^{2} - 6 y) x^{2} + (y^{2} - 6 y + 9) x^{2} + (y - 3)^{2} = 16 = 16 + 9 = 25$

But what about $x$ ? Why are there no other terms besides $x^{2}$ ? Whenever you see a missing term in an equation, you can assume there must be a zero involved; indeed, we have here the equivalent of $(x - 0)^{2}$ . Therefore, we now have sufficient information to identify the center $(h, k)$ of the circle: it is $(0, 3)$ .

We now bring in the property concerning the tangent line and the radius being perpendicular. To find the slope of the radius, we can use the center of the circle [ $(0, 3)$ ] and the point we know is on the circle [ $(3, 7)$ ]. The slope formula tells us that the slope of this line is $(7 - 3) / (3 - 0) = \frac{4}{3}$ . Since perpendicular lines have a negative reciprocal slope, the answer must be $- \frac{3}{4}$ .

For Reflection

How will you approach circle questions on test day? Write down at least three takeaways from this module.
Rate the difficulty of these questions for you from 1 (no problem) to 5 (problem!). This will help you decide when to answer them and when to skip them on test day.
This lesson is heavy with formulas and strategies. How many did you know already? Write down the ones that don’t feel automatically, especially those that are not included in the CLT’s list.