Unit Circle Trigonometry | Geometry

Introduction

Unit circle trigonometry describes this lesson completely in one sense, because everything you’ll see here is either directly about the unit circle or derived from it. But it’s helpful to mention two major topics that are derived from the unit circle and featured here: trigonometric identities and sinusoidal (sine and cosine) graphs. Identities questions will typically feature two major equations given in the CLT reference: the Pythagorean identity and the relationship of tangent to sine and cosine. We include those below. Questions about the graphs of sine and cosine will typically ask about transformation of those graphs–that is, moving up, down, left, or right or compressing/stretching the graph vertically or horizontally. But most of the questions in this category are about the details of the unit circle directly, so we’ll cover in detail how best to master unit circle content.

Approach Question

Which of the following is NOT equivalent to $cot 7 π /4$ ?

A. $\frac{c o s 3 π}{s i n ( π /2 )}$
B. $sin π - sin^{2} π - cos^{2} π$
C. $\frac{t a n ( 3 π /4 )}{t a n ( 7 π /4 )}$
D. All of the above are equivalent to $cot 7 π /4$ .

Explanation

Attention: if you have never learned about the unit circle, it’s best to stop at this point, without trying to understand this question, and look at the resources recommended in the special section “Unit Circle Foundations” below. This is question is the tip of the iceberg pointing up out of the water and there’s a hulking foundation below the surface that you must be familiar with first!

Also, a strategy note worth saying before you proceed: the topics in this lesson account for an average of 2 questions out of the 40 on the CLT Quantitative Reasoning, and they are usually among the hardest questions. Many, if not most, CLT students will find that they can garner the score improvement they’re looking for on the math section without investing the time in learning about the unit circle and trig identities. So consider carefully how, and if, you’ll use this module. With that said, if you’re ready to review the unit circle and the trig identities derived from it, please read on!

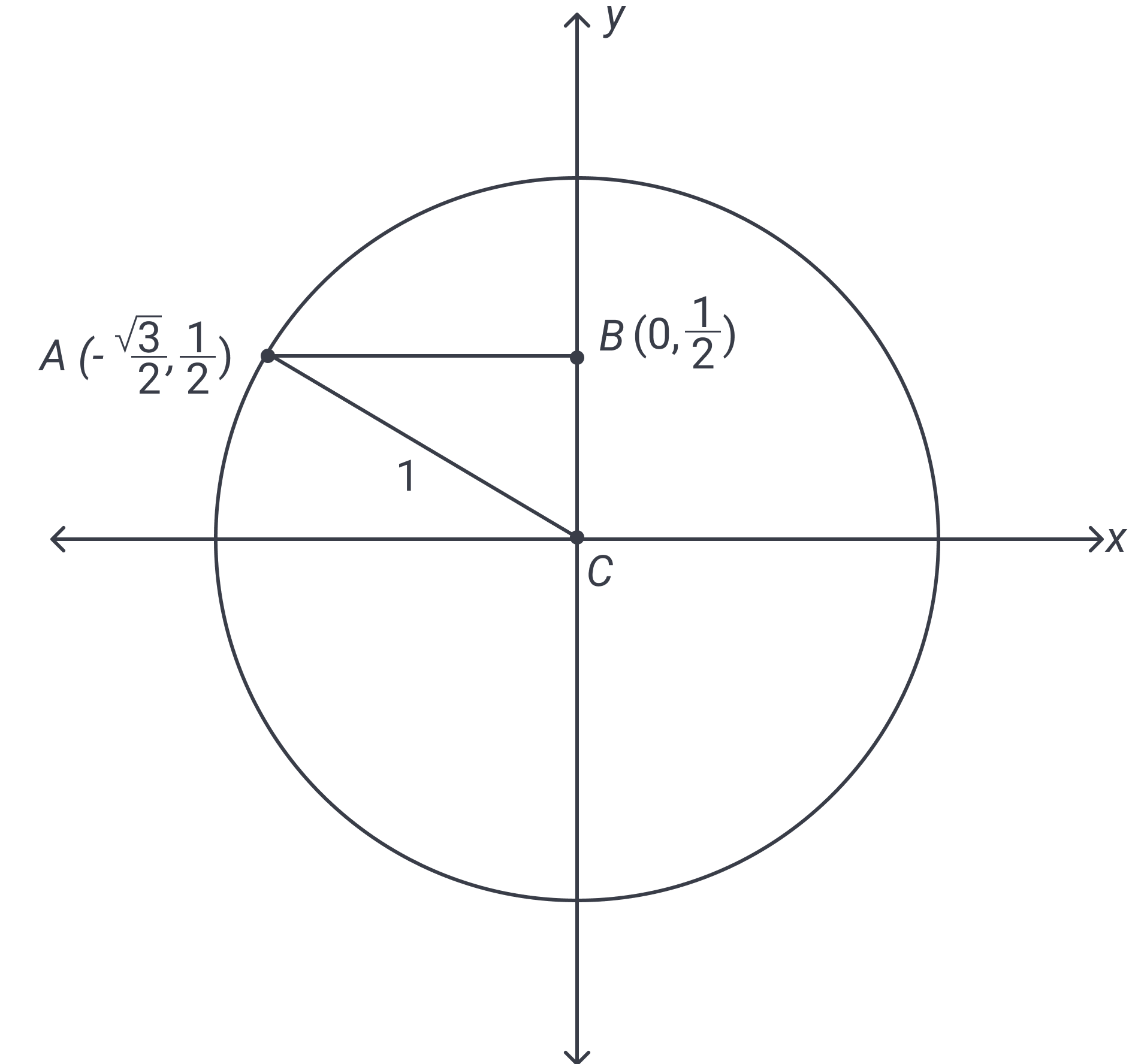
This question calls on us to pull up the mental picture of the unit circle you may have in your head: or, at least, you had it firmly in your head when you were called upon to fill out the unit circle for a quiz or test! The first thing to assess is the original value: $cot (7 π /4)$ . Recall that all trig ratios should be converted to sine and/or cosine in order to find the correct unit circle values. As the CLT reference index notes, cotangent is the reciprocal of tangent. If it’s true, then, that $t an = \frac{s in}{cos}$ (also given in the CLT reference), then cotangent must be equal to $\frac{cos}{s in}$ . We find our way to $7 π /4$ on the unit circle and discover that, in that place in Quadrant IV, $cos = \frac{2}{2}$ and $sin = - \frac{2}{2}$ . Dividing cosine by sine gives us $- 1$ ; this is the value to which we will compare all the answers.

For Choice $A$ , it’s important to remember that we can travel around the unit circle as many times as we like, and therefore the radian measures given may be more than $2 π$ . Since $3 π = 2 π + 1 π$ , we know that cos $3 π$ is the same as $cos π$ , which is $- 1$ . The sine of $π /2$ , meanwhile, is $1$ , so we divide $- 1$ by $1$ to get $- 1$ . This is not our answer since it is is equivalent to $- 1$ .

Choice $B$ contains a hidden trig identity, one given in the CLT reference. But before we encounter that, let’s first calculate $sin π$ , which is $0$ . After that value, we have something close to, but not quite, $sin^{2} x + cos^{2} x$ , which the CLT reminds us is equal to $1$ . How can we turn the expression $- sin^{2} - cos^{2}$ into what we want? Simply factor out a $- 1$ . Using the $0$ we already determined, this gives us $0 - 1 (sin^{2} π + cos^{2} π$ ), which reduces to $0 - 1$ and is therefore $- 1$ . Also not our answer. (Note that it doesn’t matter what radian measure follows both $sin^{2}$ and \cos^2$ in this case; it only matters that both values are the same. We could replace the two “ $π$ ’s” with any other pair of identical radian measures and the identity would still be equal to $1$ .)

Choice $C$ brings in tangent for the first time, which we have already identified as equal to $\frac{s i n}{c o s}$ . $sin 3 π /4$ (in Quadrant II) is $\frac{2}{2}$ , while $cos (3 π /4)$ is $- \frac{2}{2}$ . So $tan (3 π /4) = \frac{- 1}{1} = - 1$ . Meanwhile, $tan (7 π /4)$ is also $- 1$ because in Quadrant IV the sine and cosine values are simply reversed from those of Quadrant II (cosine is $1$ and sine is $- 1$ ). So we are ultimately dividing $- 1$ by $- 1$ , which is $1$ . C is our answer since it is not equal to $- 1$ .

(We can, of course, rule out answer $D$ , but it’s worth noting that the presence of an answer like this, just like the “cannot be determined” answer choice, should ideally make you extra cautious about selecting one of the other answers; time permitting, you should double-check and make sure that one of the answers is certainly correct.)

Definitions

Radian Measure: Technically defined as a “unit of angular measure”; for purposes of the unit circle, remember that $π$ radians = $180°$ . Both radians and degrees are ways of measuring the angle between the initial and terminal sides.
Quadrantal Angles: The angles on the unit circle exactly between (rather than inside) quadrants: so $90°/ (π /2)$ , $180°/ π$ , $270°/ (3 π /2)$ , $360°/2 π$ .
Initial Side: The ray that extends from the origin across the $x$ -axis in the positive direction. This is where we begin counting and, therefore, where both the degree and radian measure are equal to $0$ .
Terminal Side: The radius of the unit circle rotating counterclockwise and creating the all-important angle between this side and the initial side.
Sinusoidal: The technical definition for the curve or wave that maps the relationship between angles and their sine values. Since the cosine wave has so many similar properties to the sine wave, it is often included informally in this category as well.

Topics for Cross-Reference

Variations

As mentioned in the introduction, questions on 1) trig identities and 2) sine and cosine waves concern information derived from the unit circle. The better you know the unit circle itself, the better you’ll be prepared for these types of questions, although it is possible to memorize the necessary material for them apart from the unit circle.

A Primer on the Unit Circle

unit circle

For utmost confidence on the questions given in his lesson, there is no substitute for memorizing the entire unit circle. We provide one here and encourage you to study it, then print out a blank unit circle from a site like this one, then repeat the process as many times as necessary. However, there are a few helpful principles and shortcuts that can make your unit circle study more effective:

Begin by memorizing the radian values. You might label $π$ and $2 π$ right away, as halfway and all the way around the circle. But a universal method is to learn that $π /6$ is the first marker and is the same as $30°$ ; after that, every $30°$ increase is an increase of $π /6$ . So you can label the entire outside of the circle as $2 π /6$ , $3 π /6$ , $4 π /6$ , $5 π /6$ , etc. and then reduce the fractions that are reducible (for example $2 π /6$ becomes $π /3$ ).
Start by learning the quadrantal angles at $0$ , $π /2$ , $π$ , $3 π /2$ , and $2 p i$ (note: we will speak in terms of radians in this lesson as they are used more frequently than degrees with the unit circle). If you understand that the unit circle’s center is at the origin and its radius is $1$ , it should be natural to memorize that $π /2$ is “up one” so the coordinates are $(0, 1)$ ; $π$ is “left one” so the coordinates are $(- 1, 0)$ , etc.
Now focus on Quadrant I and memorize the values at $π /6$ , $π /4$ , and $π /3$ . You can even shorten this process by noting that the coordinates at $π /3$ are simply the reverse of those at $π /6$ ; this makes sense because (to speak in terms of degrees for a moment) $60°$ and $30°$ are complementary, and we know that for complementary angles, the sine of one is always the same as the cosine of the other). Note also that $π /4$ (or $45°$ ) must have two identical coordinates because it is derived from an isosceles right triangle where the legs are equal.
Now memorize the signs (positive/negative) in each quadrant. You probably already know the signs in each quadrant (for example that Quadrant III is negative for both x and y), but it’s helpful to associate those signs with sine, cosine, and tangent. To do so, remember the mnemonic All Seniors Take Calculus as you go from Quadrant I counterclockwise to Quadrant IV. In Quadrant I All signs are positive; in Quadrant II it’s only Sine; in Quadrant III it’s only Tangent; in Quadrant IV it’s only Cosine.
There is a straightforward way for you to infer the rest of the values from the values in Quadrant I. Imagine drawing horizontal lines across the circle one from labeled value to another. So $π /6$ connects to $5 π /6$ , $π /3$ connects to $2 π /3$ , etc. The values connected by horizontal lines must be exactly the same except for sign changes necessitated by the quadrant in which the angle is found. This helps you fill in all the remaining values based on the steps above, without having to memorize them individually.
For extra reinforcement, remember that for all the non-quadrantal angles on the unit circle (such as $π /6$ , $π /4$ , and $π /3$ ), you can derive the values of sine and cosine by drawing special right triangles inside the unit circle. The radius of each of these triangles is $1$ ; a $30 - 60 - 90$ triangle provides the values for $π /6$ and $π /3$ , while the $45 - 45 - 90$ supplies the values for $π /4$ . This is likely the way you first encountered the unit circle: by understanding how its values are derived from special right triangles and SOHCAHTOA.

Strategy Insights

See above in a Primer on the Unit Circle for strategies for learning the unit circle.

Flashcard Fodder

Unit circle trig formulas provided by the CLT on test day:

$tan θ = \frac{s i n θ}{c o s θ}$

$csc θ = \frac{1}{s i n θ}$

$sec θ = \frac{1}{c o s θ}$

$cot θ = \frac{1}{t a n θ}$

$sin^{2} θ + cos^{2} θ = 1$

Right triangle formulas NOT provided by the CLT on test day:

Although the CLT reference mentions that there are $360$ degrees in a circle and $2 π$ radians in a circle, it doesn’t make it explicit that, therefore, $π$ radians equal $180$ degrees and therefore we can do the following:

To convert from degrees to radians: multiply by $π /180$

To convert from radians to degrees: divide by $180/ π$

Here are the forms of the so-called “sinusoidal” functions: the sine and cosine waves, along with a key to understand each coefficient:

$f (x) = a sin b (x - c) + d$

$f (x) = a cos b (x - c) + d$

$a$ = amplitude: the distance from the horizontal midline of the graph and either the top or bottom of the graph

$2 π / b$ = period: the distance along the x-axis that it takes for the waves to complete one full revolution (in other words, after one revolution the wave “starts over”)

$c$ = phase shift: the shift left or right (note the minus sign! $x - π$ , for example, would be pi to the right)

$d$ = vertical shift: the shift up and down (here the wave doesn’t differ from any other graph, such as a line or a parabola

Sample Questions

Difficulty 1

For a given angle $θ$ , $cos θ = - 1$ . What is the value of $sin θ$ ?

A. -1
B. 0
C. 1
D… It is impossible to determine from the information given.

(spoiler)

The answer is B. The so-called “quadrantal” angles are some of the most natural on the unit circle since they correspond to “up one”, “left one”, “down one”, and “right one” from the origin. The additional piece of information we need is that cosine corresponds to $x$ values on the unit circle while sine corresponds to $y$ (if you need a mnemonic for that, note the “cosine” comes before “sine” alphabetically just as $x$ comes before $y$ ).

So if $cos θ = - 1$ , we are looking for the place in the unit circle where the $x$ -coordinate. Between $0$ and $2 π$ there is only one such angle: $π$ radians. At that angle, sine is always $0$ because the location is on the $x$ -axis, neither above it nor below it.

It’s possible that choice $D$ could be tempting if you’re thinking that there are many angles ( $3 π$ , $5 π$ , $7 π$ , etc.) where $cos θ = 1$ . That’s true, but sine is always equal to $0$ at those values, so we can determine a fixed value for sine.

An interesting alternate strategy is to consider the Pythagorean identity, $sin^{2} θ + cos^{2} θ = 1$ . How so? It gives us a relationship between cosine and sine. According to this identity, $sin^{2} θ = 1 - cos^{2} θ .$ And if $cos θ = - 1$ in this problem, then $cos^{2} θ = 1$ . Plugging that into the identity shows us that $sin^{2} θ = 0$ , which has to mean that $sin θ = 0$ .

Difficulty 2

Which of the following is equivalent to $\frac{1}{s e c θ}$ ?

A. $sec θ$
B. $sin θ$
C. $tan θ \times csc θ$
D. $cot θ \times sin θ$

(spoiler)

The answer is D. This is an example of a trigonometric identity question, where we’ll use equivalent trig-based statements to try to make one expression look exactly like another. As noted in Flashcard Fodder, the most common trig identities are $sin^{2} θ + cos^{2} θ = 1$ and $tan θ = \frac{s i n θ}{c o s θ}$ . There are also the reciprocal trig functions, helping us in this case realize that with $\frac{1}{s e c}$ we’re really just dealing with cosine. All of these identities are given in the CLT reference, so it’s mostly a matter of applying them rather than memorizing (though memorizing will give you a speed bonus!).

The task is to find which choice is the same as $cos θ$ . Choice $A$ is reciprocal of what we want, and choice $B$ is simply sine, which is not the equivalent of cosine. Choices $C$ and $D$ require some translation. For Choice $C$ , let’s change tangent and cosecant into their equivalent identities so that we rewrite the expression as follows:

$\frac{s i n θ}{c o s θ} \times \frac{1}{s i n θ}$

Multiplying and canceling gives us $\frac{1}{c o s θ}$ , which is $sec θ$ . Not the same as cosine.

It must be choice D, but let’s confirm. $cot θ$ can be rewritten as $\frac{c o s θ}{s i n θ}$ ; multiplying this fraction by $sin θ$ cancels the sines and leaves just cosine. Bingo!

Difficulty 3

The center of a certain circle is labeled $C$ . Point $A$ is on the circle at coordinates $\frac{- 3}{2}$ , $\frac{1}{2}$ . Point $B$ is the $y$ -intercept of the line $y = 3 x + \frac{1}{2}$ . If $A C = 1$ , what is the degree measure of $∠ B A C$ ?

A. 30°
B. 45°
C. 60°
D. 90°

(spoiler)

The answer is A. This is certainly a question you should draw out! Your diagram should look something like this:

circle with center labeled C and point A and point B

This problem, admittedly, can be solved without unit circle trig principles. If you realize that side $BC$ must have a length of $\frac{1}{2}$ and side $A B$ must have a length of $\frac{3}{2}$ , then the sides bear the marks of a $30 - 60 - 90$ triangle. It only remains, then, to discover that angle $A$ is the smallest angle of the triangle because it is across from the shortest side ( $\frac{1}{2}$ ). Angle A must therefore measure $30°$ .

How does unit circle thinking support this answer? It’s worth reinforcing here the concepts of the initial side and the terminal side of angles in the unit circle. The initial side of the angle in the unit circle is simply the $x$ -axis to the right side of the origin; this initial side never moves. The terminal side is the radius of the circle moving counterclockwise away from the initial side so that it creates an angle (sometimes known as the terminal angle but usually just referred to as “an angle,” since it’s typically the only one being considered). Noting that the only radius drawn in our figure is line segment $A C$ , we can use the coordinate values given to identify the angle between initial and terminal sides in this case. The coordinates reveal that our angle is $\frac{5 π}{6}$ or, more helpfully in this case, $150°$ . How does this help us? If we take away from this angle the $90°$ angle that resides in the portion in Quadrant I, we see that angle $BC A$ is $60°$ . This means that, since this is a right triangle, that angle $B A C$ must measure $30°$ .

Difficulty 4

A student is studying the unit circle and comes up with the following conjecture:

If the radian measure of an angle is more than $π$ , the sine of that angle is always negative.

Which of the following angles provides a counterexample to the student’s conjecture?

A. $7 π /4$
B. $9 π /4$
C. $13 π /4$
D. $15 π /4$

(spoiler)

The answer is B. The student here has made a very understandable error. Our “All Seniors Take Calculus” memory device shows where sine is negative: Quadrants III and IV (since only tangent is positive in the former and only cosine is positive in the latter). Following our markers of radian measure, it does indeed appear that, once we cross the “ $π$ radians” threshold, sine is always negative. But the student has forgotten that we don’t have to stop with just one revolution! Answer choices $B$ , $C$ , and $D$ illustrate how we can start a second revolution around the unit circle: once we cross the $2 π$ threshold, we are back in Quadrant I, where sine is positive. So $B$ is our answer. By the time we continue traveling around the unit circle to where choice $C$ and $D$ take us, we have descended once again below the $x$ -axis into Quadrant III (choice $C$ ) or Quadrant IV (choice $D$ ). So those choices are excluded.

If you fell for that trap, know that you’re in good company. Harder CLT questions often deal with rare exceptions that are easy to overlook. But if you use the UnCLES well and always carefully consider all the answers, you will be less vulnerable to such errors.

Difficulty 5

If $y = 5 sin (3 x) + 2$ is graphed in the ( $x y$ )-coordinate plane, how many times does the graph intersect the $x$ -axis between $x = 0$ and $x = 2 π$ ?

A. 0
B. 2
C. 4
D. 6

(spoiler)

The answer is D. We’ll reproduce the parent function here (you’ll find it in Flashcard Fodder as well): $f (x) = a sin b (x - c) + d$ . To unlock this question, we have to determine whether the question is asking about amplitude, period, phase shift, or vertical shift. If we’re looking for how many intercepts we have in a certain interval, one thing we need to determine is whether the combination of amplitude and vertical shift cause the graph to be so raised or lowered that it doesn’t cross the $x$ -axis at all. Is that true in this case? The $5$ at the front tells us the graph rises $5$ units up from the midline and drops $5$ units below. For it to miss the $x$ -axis altogether it would have to be vertically shifted more than $5$ units up or down, and this is not the case.

That leaves us with the phase shift and the period. But if you examine the function carefully, you’ll see that there is no “minus $c$ ” (or “plus $c$ ” for that matter) after the $x$ and inside the parentheses. So the phase shift is zero; it doesn’t change the typical graph.

But what is the typical graph? Remember that the sine graph is derived directly from the unit circle, Following the sine values at the quadrantal angles, we discover the points $(0, 0)$ , $(π /2, 1)$ , $(π, 0)$ , $(3 π /2, - 1)$ , and $2 π, 0)$ . (The $x$ -coordinates in these points are radian values; the $y$ -coordinates are sine values.) Take a moment to graph these five points and you’ll see the basic sine wave forming.

A tricky part of this question is that at this point the vertical shift becomes important. It reminds us we’re not starting from the original, but rather two units above it. So when the sine graph goes up at the beginning and even as it descends back to its original level, it won’t be crossing the $x$ -axis. It’s only when it dips down into its “trough” or lower part that it will cross. Do you see (with the aid of your graph as necessary) that it will cross the $x$ -axis twice during one revolution–once as it descends and ones as it ascends?

Now that we know the graph cross the $x$ -axis twice per revolution, we must determine how many revolutions are present in this interval. Here is where the period helps us, because the period is the length of one revolution. Since $2 π / b$ gives us the period, we discover that in this case the period is $2 π /3$ . How many of these periods are in the range between $0$ and $2 π$ ? We divide the $2 π$ by $2 π /3$ ; the $2$ ’s cancel with division and we’re left with $3$ revolutions. $2$ intercepts per revolution times $3$ revolutions makes $6$ total $x$ -intercepts.

For Reflection

How will you approach unit circle trig questions on test day? Write down at least three takeaways from this module.
Rate the difficulty of these questions for you from 1 (no problem) to 5 (problem!). This will help you decide when to answer them and when to skip them on test day.
Considering the advice given in the Approach Question’s explanation, do you plan to study the unit circle and try these questions day, or does it fit your goals and strategy better to skip this content? The sooner you make a final decision on this question, the better.