Angles
Introduction
Angles questions on the CLT commonly ask about angles inside shapes: triangles and quadrilaterals especially but occasionally larger polygons. They also sometimes concern angles in relationship to lines, as in straight angles and parallel lines. In these cases, the supplementary relationship (adding up to ) is very common. Identifying congruent angles, that is, angles equal in measure. often plays an important role in solving as well.
Approach Question
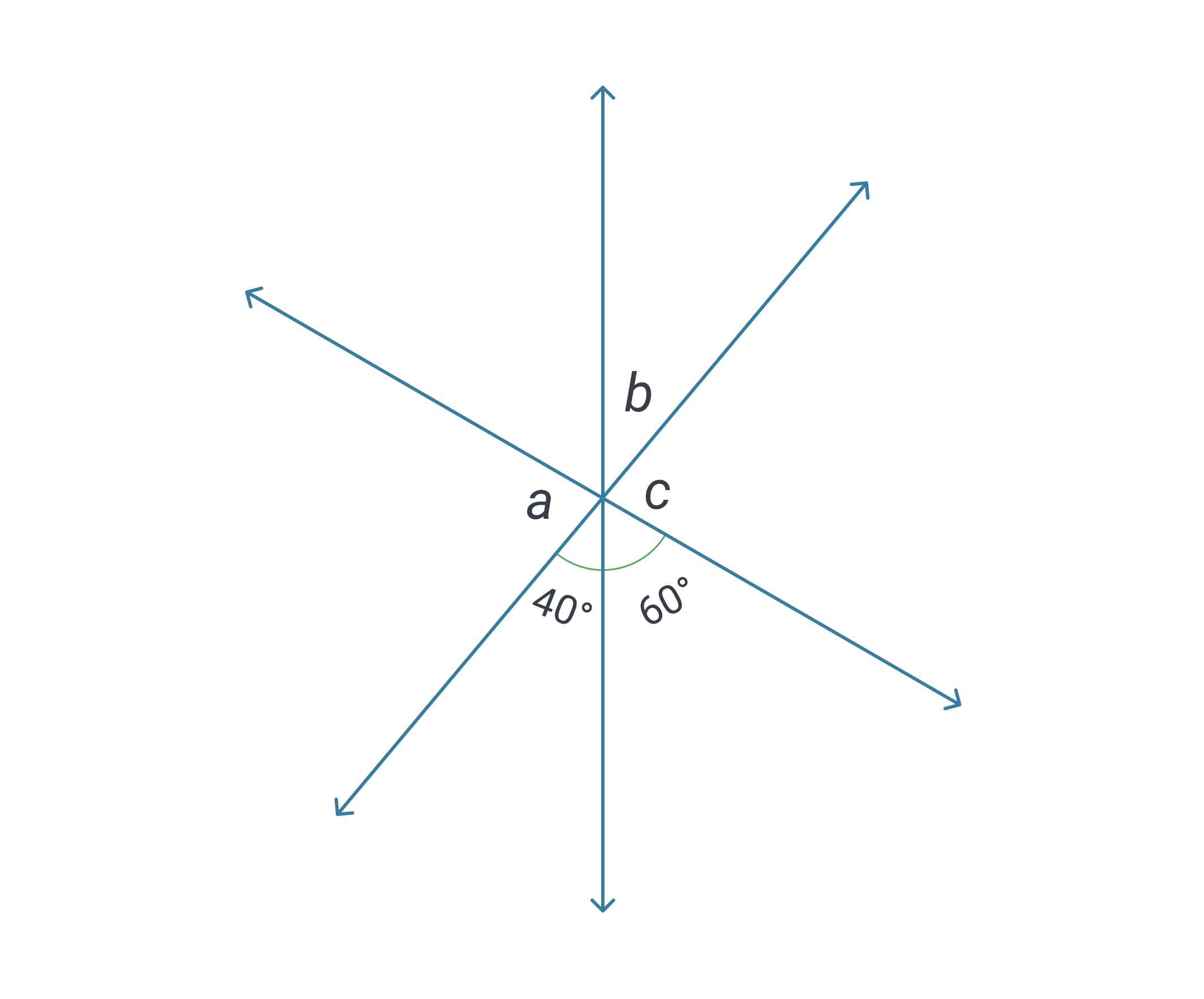
In the figure below, three lines intersect at the same point, creating the angles shown. What is the measure of angle c?
A.
B.
C.
D.
Explanation
Angles questions will draw on several different properties of angles; we will cover the most frequent of these properties in this lesson. In this case, two theorems in particular are needed. First, we need to know that angles making up a straight angle (the angle along a straight line) are supplementary, that is, they add up to . This is true no matter how many angles combine to make the straight angle. In this figure, the angles measuring and combined with angle make up a straight angle, so the three of those angles must add up to . If we subtract the two numbered angles from , remains, so that must be the measure of angle .
The second important theorem here is known as the vertical angles theorem, which tells us that two opposite angles created by the intersection of two lines must be congruent (“congruent” means equal). To find vertical angles, we look for two intersecting lines and seek the angles “across from” each other. We can see in this figure that two lines create angles and and that angles and are opposite each other. This means that the measure of angle is equal to the measure of angle , so angle is also . The answer is C.
Topics for Cross-Reference
Variations
CLT problems often use information about angles to draw conclusions about triangles or quadrilaterals. We will explore those sorts of questions in the lessons on those polygons.
Flashcard Fodder
The triangle angle sum theorem, showing that the angles within a triangle measure , is used repeatedly in this lesson. Nothing is more helpful for CLT angles problems than this theorem!
-
Quadrilaterals (polygons with four sides) have of interior angle measure.
-
Beyond four sides, polygon angle measure continues a pattern: from for three sides to for four sides, we can continue adding per added side: so a pentagon has , a hexagon , etc. If you prefer, however, memorize the following formula for the total degrees in a polygon:
Total degree measure = , where n is the number of sides
-
If you want to use the formula above but find out the measure of each of the angles in the regular polygon, simply divide by n as the number of sides. So that formula is:
Degree measure of each angle =
-
As shown in the Approach Question to today’s lesson, vertical angles (angles immediately across from each other and created by the same two lines) are congruent.
Sample Questions
Difficulty 1
One angle in a triangle measures . What is the sum of the measures of the other two angles in the triangle?
A.
B.
C.
D. It is impossible to determine from the given information.
The answer is C. The measures of the interior angles in a triangle sum to . The CLT, usually on lower-difficulty questions, will ask you to subtract existing angles from . Answer choice D might be tempting here because it’s true that we don’t have enough information to measure the other two angles of the triangle individually. But that doesn’t mean we can’t find them in combination. There are degrees left for the two angles in the triangle not yet known, so the sum of their measure must be .
Difficulty 2
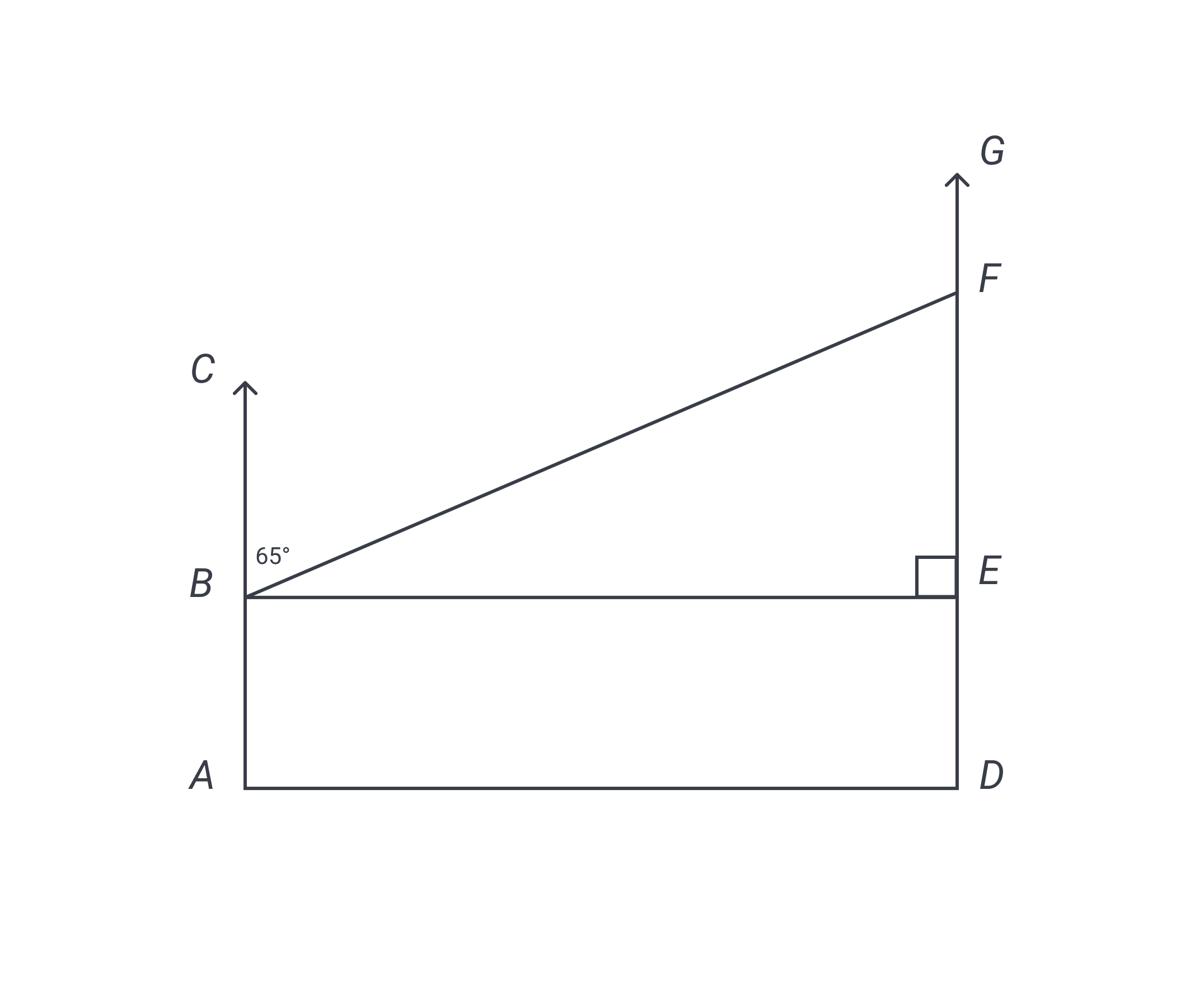
In the figure below, is parallel to and is a right triangle. What is the measure of ?
A.
B.
C.
D.
The answer is A. We can solve this problem one of two ways. Solution 1: because we know is a right angle (from the right triangle), we know line segment is perpendicular to . This means that is also a right angle, because if a certain line (let’s call it ) is perpendicular to another line (let’s call it ), then line must be perpendicular to all lines that are parallel to . If is a right angle, then we simply need to subtract that angle to get .
Solution 2: because and are parallel, and are congruent alternate interior angles. This means that the measure of is also . Knowing that two angles of our triangle are and , we can subtract them both from to arrive at .
Difficulty 3
In a certain isosceles triangle, one of the angles measures 110°. What must be the measure of the other two angles?
A. and
B. and
C. and
D. Is it impossible to determine from the given information.
The answer is B. The UnCLES method reminds us to read every word carefully; we must not overlook that this an isosceles triangle. This means that not only two of the sides, but also two of the angles, must be congruent. This knowledge eliminates choice right away, even though it does make the angles sum to . Choices and do guarantee that two of the angles are the same, but choice is a trap answer tempting to those who mistakenly think that a triangle’s angles sum to instead of .
Answer looks good, but do we have enough information to be sure this must be the case? Choice may be appealing if you’re thinking about the fact that we don’t necessarily know which two angles of an isosceles triangle are congruent. But there’s another reality operating here: a triangle can only have one obtuse angle at most, because two obtuse angles would by themselves sum to more than . So the fact that we’re already given an obtuse angle means that the other two angles must not only be acute but also have equal measures so the triangle is guaranteed to be isosceles. Though tempting, choice can be eliminated.
Difficulty 4
In , is five times and is less than twice . What is ? (Note: the “m” in this notation means “the measure of”.)
A.
B.
C.
D.
The answer is A. We begin, as it often the case, with in a triangle. But since none of the three angles is given to us precisely, we’ll do well to set up multiple equations to modeling the situation. The first sentence tells that . (Remember the principle of “help” to confirm that the smaller angle, B, is the one that gets multiplied.) The second equation is more tricky: . (Make sure you note that the phrase “ less than” translates to subtracting from the other term.)
We need to combine the equations to reduce the scenario to just one variable. Since is present in both equations, it is probably the best candidate. Solving the first equation in terms of A (isolating the other variable) leaves . We already know what is in terms of , so we can now use the in the triangle to construct the following equation:
Multiplying through by to get rid of the fraction gives us:
So:
To get angle , the smallest angle, we can simply divide by . Angle B is .
As is often true with challenging problems, there is an alternate strategy here that uses the answers and works backward. Let’s start with one of the middle answers, , and suppose that’s the measure of angle . Angle , being five times larger, must be . Angle , which is less than twice angle , comes out as . Clearly our numbers are too large for a triangle’s interior angles, which means the answer is ! How do we know this? Choice is the only answer smaller than . Note this strategy and make sure your solutions toolbox includes this backsolving approach, which takes advantage of the fact that CLT answer choices are usually listed in numerical order.
Difficulty 5
What is the measure of each of the angles in a regular octagon?
A.
B.
C.
D.
The answer is C. There is a formula for this question, which we will use in a moment, but let’s consider how you might use geometric reasoning to answer this question if you didn’t know the formula. How could you draw diagonals inside a regular octagon to help you divide its angle into recognizable portions? If we keep all our diagonals either vertical or horizontal, we’ll recognize right angles and be able to infer the measures of the other angles. Consider this figure:
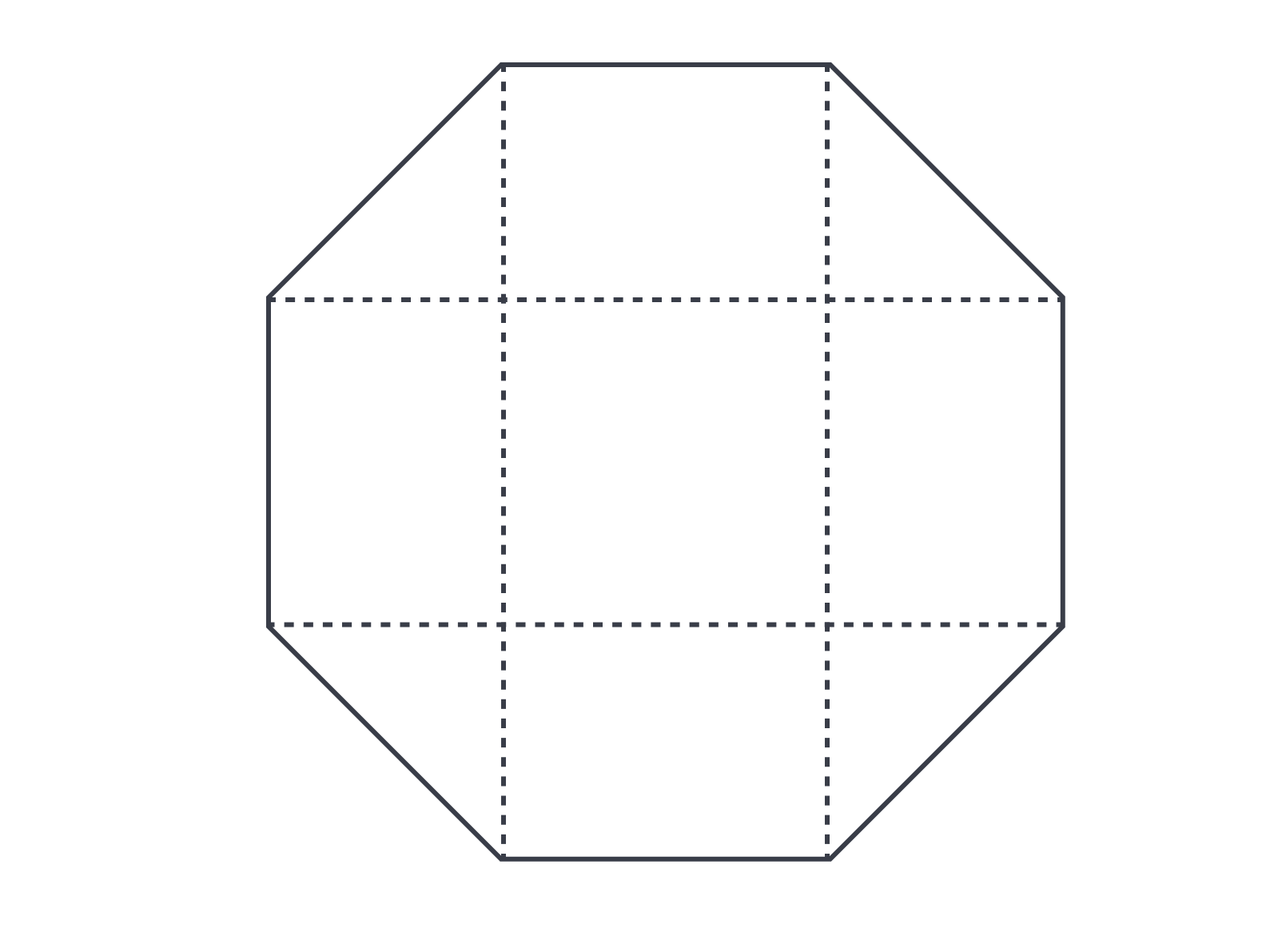
The dashed lines create several rectangles and triangles; knowing that a rectangle’s angles are all allows us to locate a right angle making up part of each of the octagon’s interior angles. What is the measure of the other part? If all the interior angles are going to be equal, then the part added to in each angle must be the same. But that angle also constitutes, in the case of each of the four triangles, the two non-right angles. The non-right angles must always add up to , so in this case each smaller angle must be . So each interior angle of a regular octagon must measure .
We summarize the strategy above to help you see that there are ways to solve geometry questions using logic and sketching even when you don’t know the relevant formula. But, of course, the relevant formula is much faster in this case:
Angle measures in a regular polygon = , where n is the number of sides.
Plug in for and, with a little calculation, you get .