Parallel lines with a bisector

Parallel lines are lines that never intersect each other no matter how far they extend. A transversal is a stray line that intersects two parallel lines. This section focuses on the rules regarding transversal lines intersecting parallel lines. These rules are important because they allow us to determine the measure of an angle by using other relevant information.

Transversal lines

Supplementary angles

The sum of all the angles on one side of a line is equal to 180 degrees. So, if we have two parallel lines with a transversal intersecting them, we will have to sum together both angles on a side of a line to a total of 180. These are called supplementary angles and they add up to $180$. If we do not know the measure of one angle, we can find it by using this rule:

What is the measure of angle $x$ below?

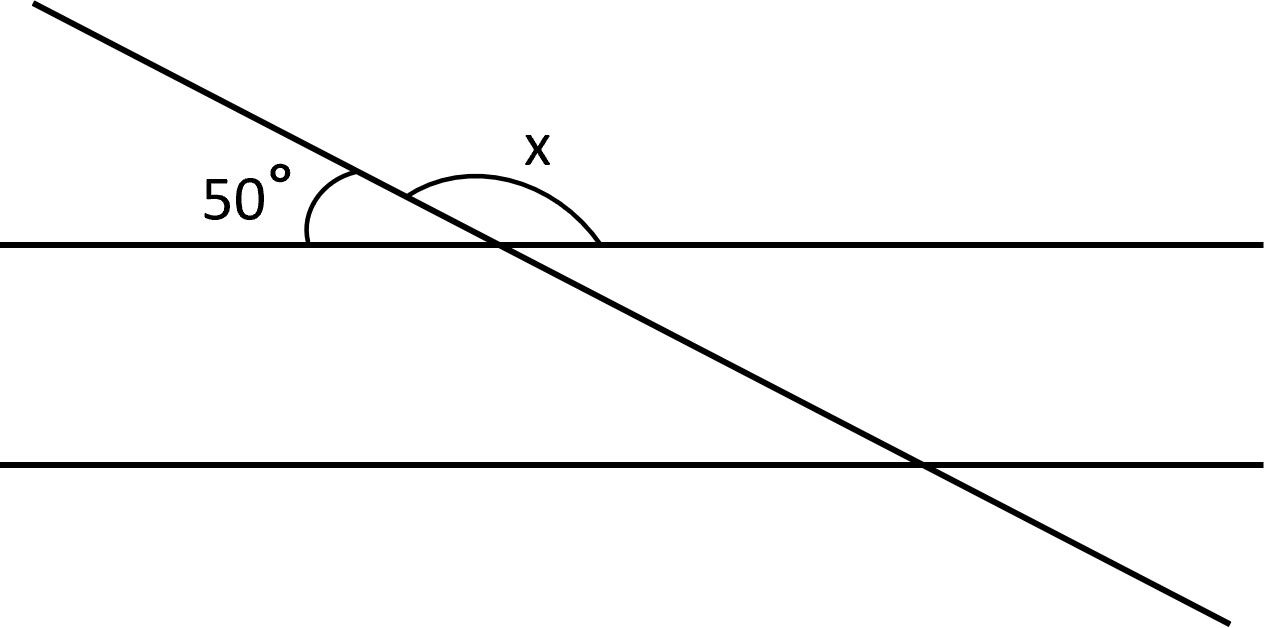
We know that the sum of the two angles is 180 degrees. So, we can formulate the following equation:

$$50+x=180$$

Using this equation, $x$ is equal to 130 degrees. This is the law of supplementary angles applied to transversals.

Angle relationships

In the case of two parallel lines and a transversal, all angles that are diagonally touching are equal to each other. That means that the angle opposite the angle $x$ in the example above is also equal to $130$, and the angle opposite the 50-degree angle is also 50 degrees.

Likewise, the four angles at the first intersection point are equal to the four angles at the second intersection point. The figure below describes which angles share the same value. All red angles share the same value, and all blue angles share the same value:

Non-parallel lines with a transversal

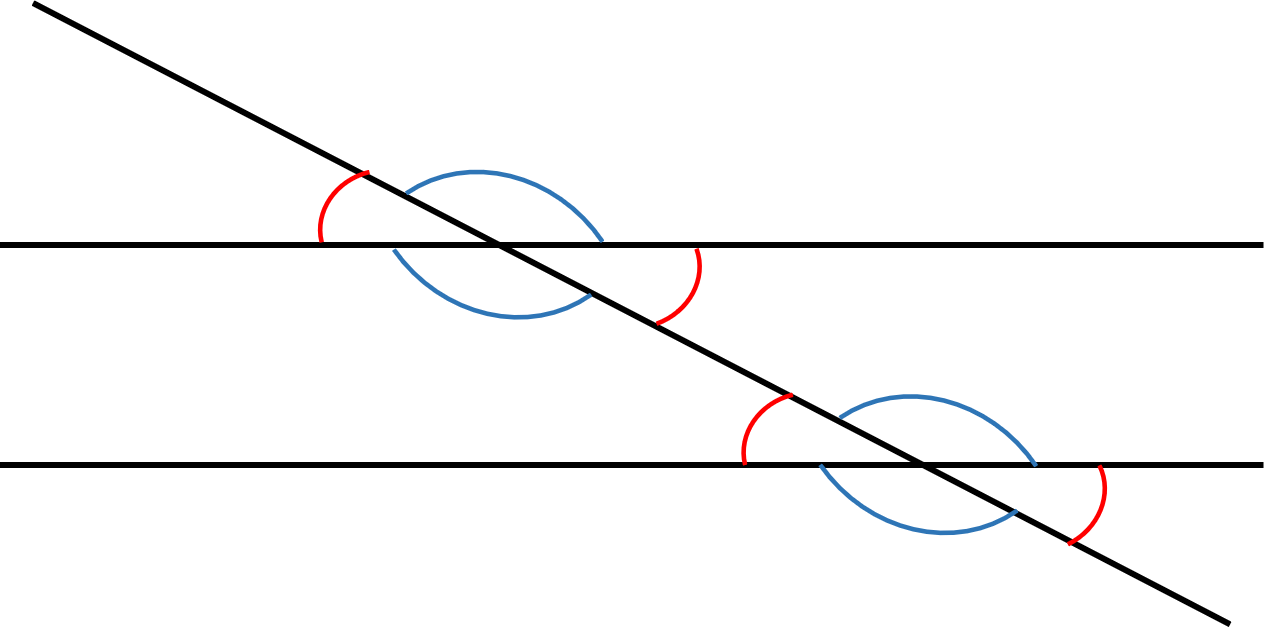
Sometimes you will be given two lines that are not parallel with a transversal. These are the same as parallel lines, except that the angles around the transversal on each line will only be equal to the angles that are diagonal from each other. Like in the image above, the top two blue angles will be equal, but they will not be equal to the bottom two blue angles.