Conic sections

A conic section is the shape we get when we cut a slice out of a cone. For the purposes of preparation for the ACT or SAT test, you will only need to know parabolic, circular, and elliptical cross sections. They look like this:

This chapter will not so much focus on how these cross sections are made, but rather on how to use them. You may already have extensive knowledge of solving parabolic equations. If not, visit the chapter Solving quadratic equations before continuing this chapter, as we will only discuss circular cross sections in further detail.

Circular cross-sections

A circle can be described by an equation, just like a parabola can. This equation looks like the following:

$$(x-a{)}^2+(y-b{)}^2=r^2$$

Now we can simplify this equation depending on where our circle is located. If our circle is centered at the origin, then it simplifies as follows:

$$x^2+y^2=r^2$$

Now, we have a few things to note here in order to fully understand the equations of circles.

Equation of a circle: center

In the equation of a circle, $x$ and $y$ are coordinate directions, $r$ is the radius, and $a$ and $b$ are the coordinates of the center of the circle. This is why the simplified version of the equation, where the center of the circle is at the origin, eliminates $a$ and $b$: they are both equal to $0$.

In most other cases, the center of the circle will have to be determined using $a$ and $b$. The variable $a$ corresponds to the $x$-coordinate and the variable $b$ corresponds to the $y$-coordinate. Let’s review a quick example:

Find the center of the circle given by the following equation:

$$(x-4{)}^2+(y+3{)}^2=36$$

Here, $a$ is equal to $4$ and $b$ is equal to $-3$. This means that the center of our circle is located at the point $(4,-3)$.

Equation of a circle: radius

One of the simplest yet most forgotten details of the equation of the circle is the condition of the radius. You’ll notice that in the equation the radius is squared. This means that the number to the right of the equal sign is the square of the radius, and we will need to take the square root of that number to find the actual radius.

Referring to the above example, $(x-4{)}^2+(y+3{)}^2=36$, what is the radius of the circle?

Let’s do one more example that is a bit less obvious:

A circle is described by the following equation:

$$(x-1{)}^2+(y-1{)}^2=144$$

What is the circumference of this circle?

This question wants us to find the circumference, but in order to do so we must first determine the radius. Try solving it step-by-step, then check your answer below.

Also, note that a similar method can be done for parabolas. Quadratic functions can also appear in vertex form where they directly give the vertex of the parabola in the form below:

$$y=a(x-h{)}^2+k$$

The vertex here is $(h,k)$. More information about this form is in the chapter “Vertex form equation ($a$, $h$, and $k$)”.

Elliptical cross sections

An ellipse is essentially a flattened circle. It is a circle that has been modified so that it is wider or taller than a perfect circle. You will need to be familiar with the equation of an ellipse and what each term represents.

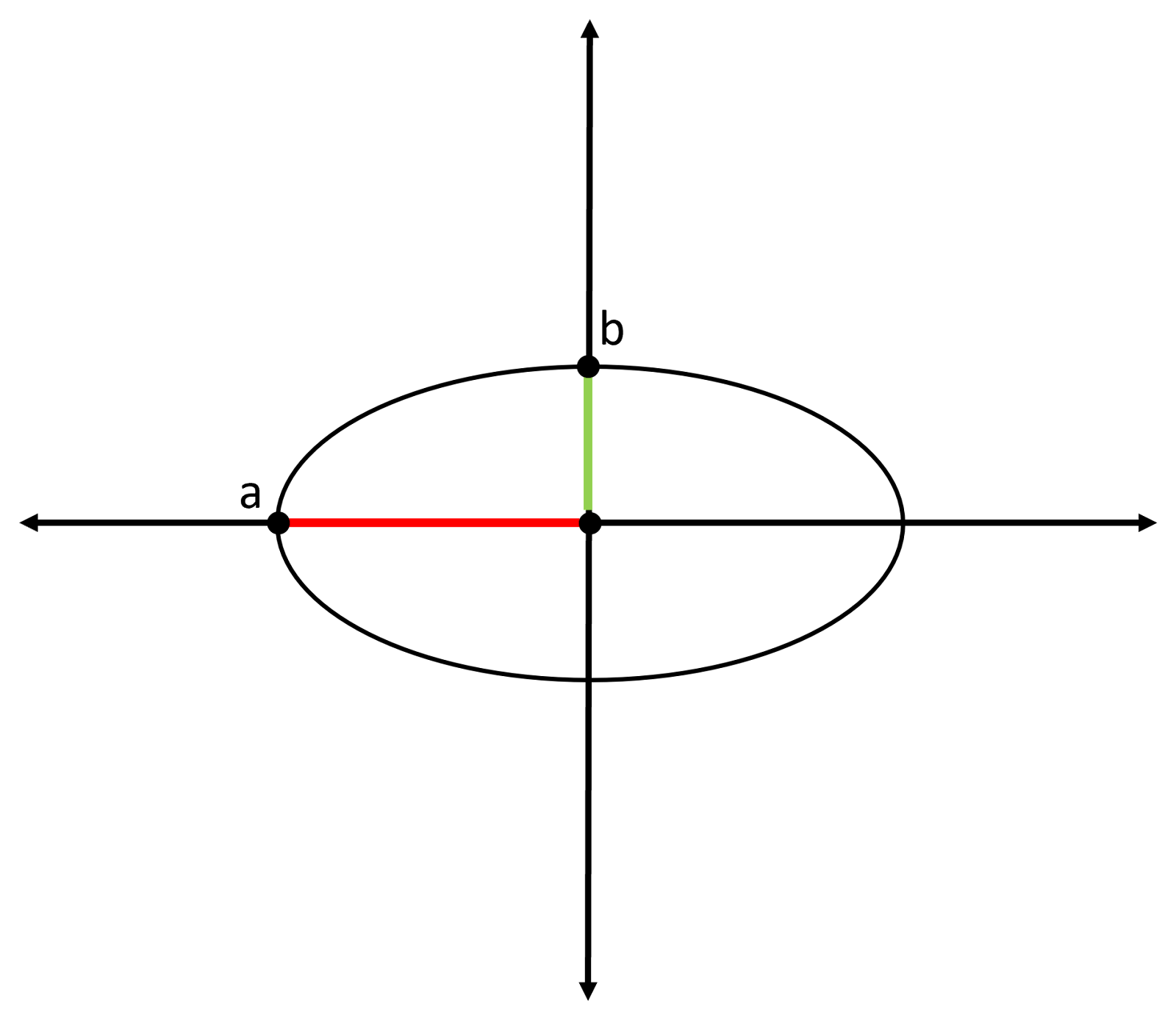
The equation of an ellipse can tell you the way in which the circle is stretched. The letter $a$ represents the length from the center to the tip of the curve in the $x$-direction and the letter $b$ represents the length from the center to the tip of the curve in the $y$-direction. The remaining parameters are the same as with the equation of a circle. Below is the equation of an ellipse:

$$\frac{(x-h{)}^2}{a^2}+\frac{(y-k{)}^2}{b^2}=1$$

Remember that $a$ represents the $x$-direction and $b$ represents the $b$ direction. This means that if $a$ is larger than $b$, the ellipse is wider than it is tall. This is like the image that is shown below. Conversely, if the $a$ is smaller than the $b$, then the ellipse is taller than it is wide. Just remember that $a$ and $b$ are positioned below the variable that they modify (e.g., in $\frac{(x-h{)}^2}{a^2}$, $a$ has to do with the $x$-direction). This means that if $a$ and $b$ are equal, what you get is a circle! That’s right, all equations are technically ellipses, but not all ellipses are circles.

Visualization

To better visualize the values of $a$ and $b$, see the following image: