Triangle geometry

All triangles have a few geometric rules in common. First, all angles in a triangle must add up to 180 degrees. This means that the three angle measurements within any given triangle must sum to $180$. Second, the area of any triangle is equal to one-half the product of its base times its height $(\text{Area}=\frac{1}{2}(\text{base}\times \text{height}))$.

Triangle inequality theorem

Occasionally you’ll be given a few side lengths and asked to determine if they can make up a triangle. To find this out, you’ll need to use something called the triangle inequality theorem. To use this theorem, we add the two smaller side lengths and see if that is larger than the third side. If the two sides are longer than the longest side, the triangle inequality theorem is satisfied and we can say that the side lengths do make a triangle.

Let’s do a quick example.

Do the three following side lengths make a triangle?: $7,8,14$

The sum of $7$ and $8$ needs to be larger than $14$. We can write this like a formula:

$$\begin{array}{rl}7+8& >14\\ 15& >14\end{array}$$

So these side lengths do form a triangle. An example of side lengths that do not form a triangle are $7$, $8$, and $18$ because $7+8=15$, which is smaller than $18$.

There are also a few extra rules that apply only to certain types of triangles. These will be examined below.

Equilateral triangles

Equilateral triangles have all three sides equal to each other and all three angles equal to each other. So, if you are missing any lengths or angle measurements, you can remember that they are all equal to one another in an equilateral triangle.

Isosceles triangles

These triangles have two sides equal to each other and two angles equal to each other. So, if you know one of the equivalent sides, you know the other as well. The same is true for the equivalent angles.

A common problem involving isosceles triangles is finding all the angle measurements when given just one angle. Knowing that the sum of all angles is 180º, you can solve for all angles in an isosceles triangle given just one angle. As a result, it is very important to recognize if a question labels a triangle as an isosceles triangle.

Scalene triangle

Scalene triangles are the most difficult triangles to work with. There are no equivalent angles or sides. Questions involving these triangles often include multiple triangles that are related to each other in some way. This relationship may include congruency or similarity.

Congruency and similarity

When comparing two triangles together, it is important to note the qualities that they have in common. If two sides, angles, or triangles are congruent, it means that they have the same values. If two triangles are similar, it means that they have the same angle measurements but different lengths of sides.

Congruency

If two qualities of a triangle are congruent, this will be indicated by identical hatch marks, like below:

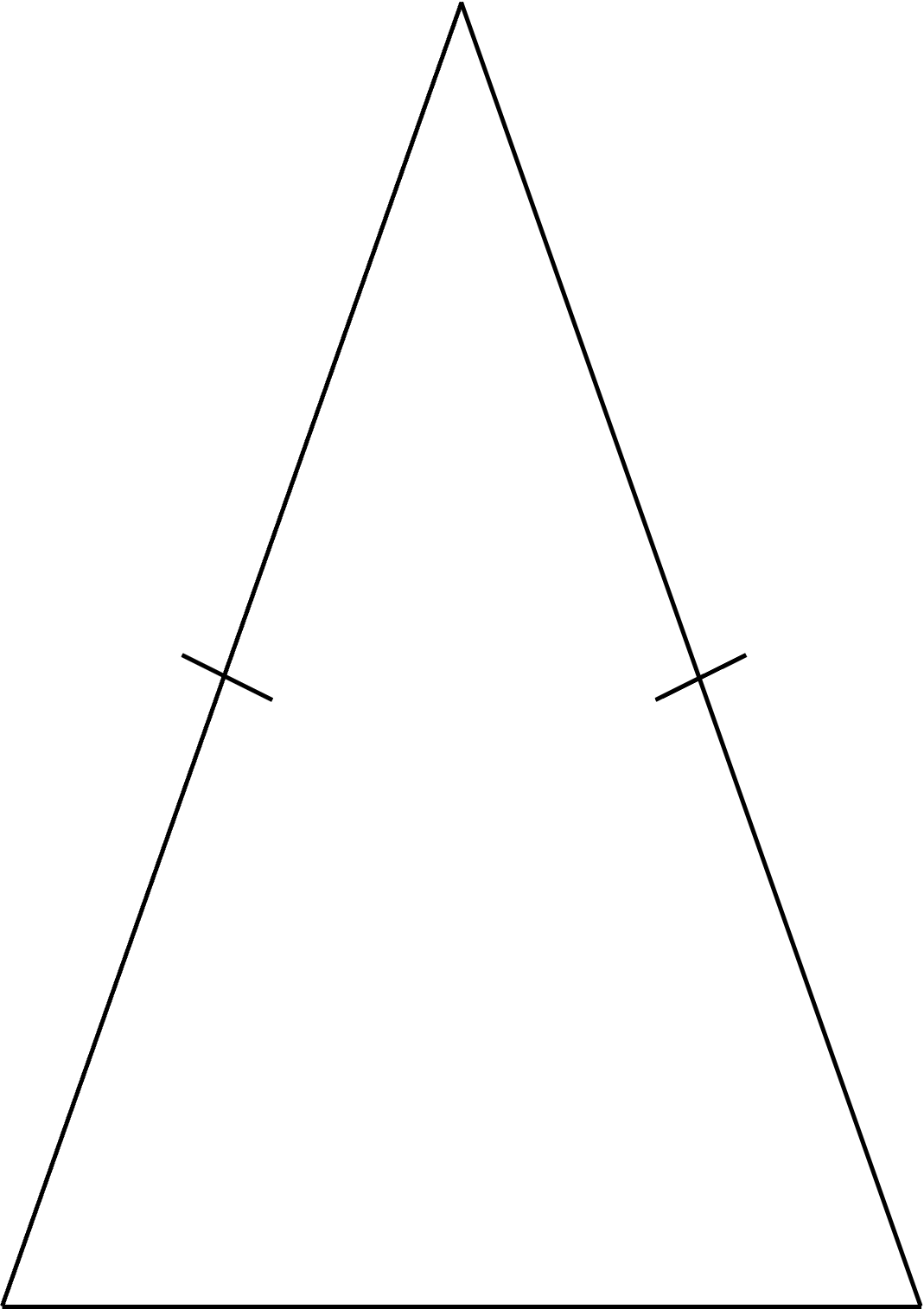
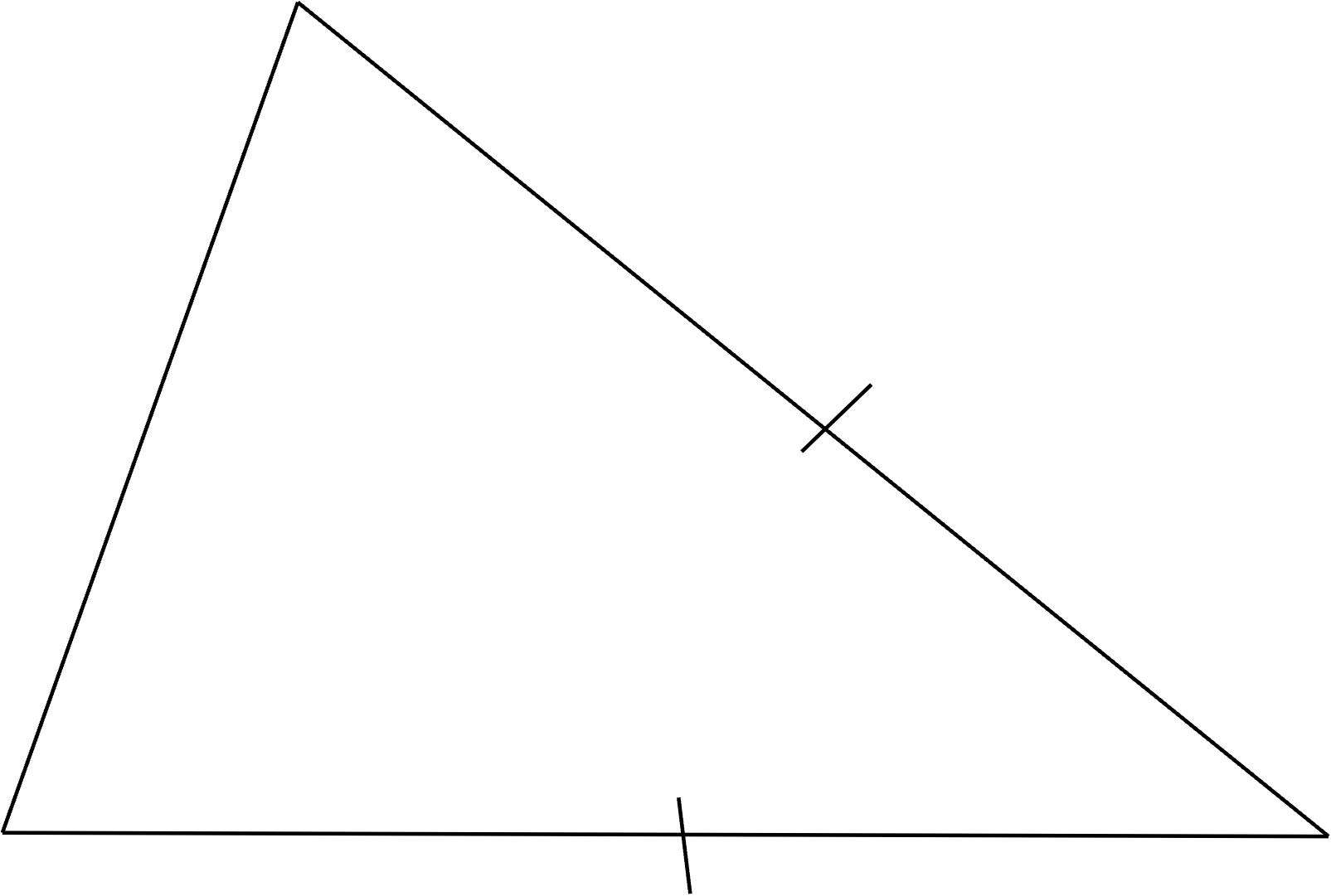
Two different triangles may share congruent qualities, as well. The same indication is used:

Let’s do an example involving congruent angles. If measure of angle $B$ is equal to 50º, find the angle measure $x$ in the triangles below:

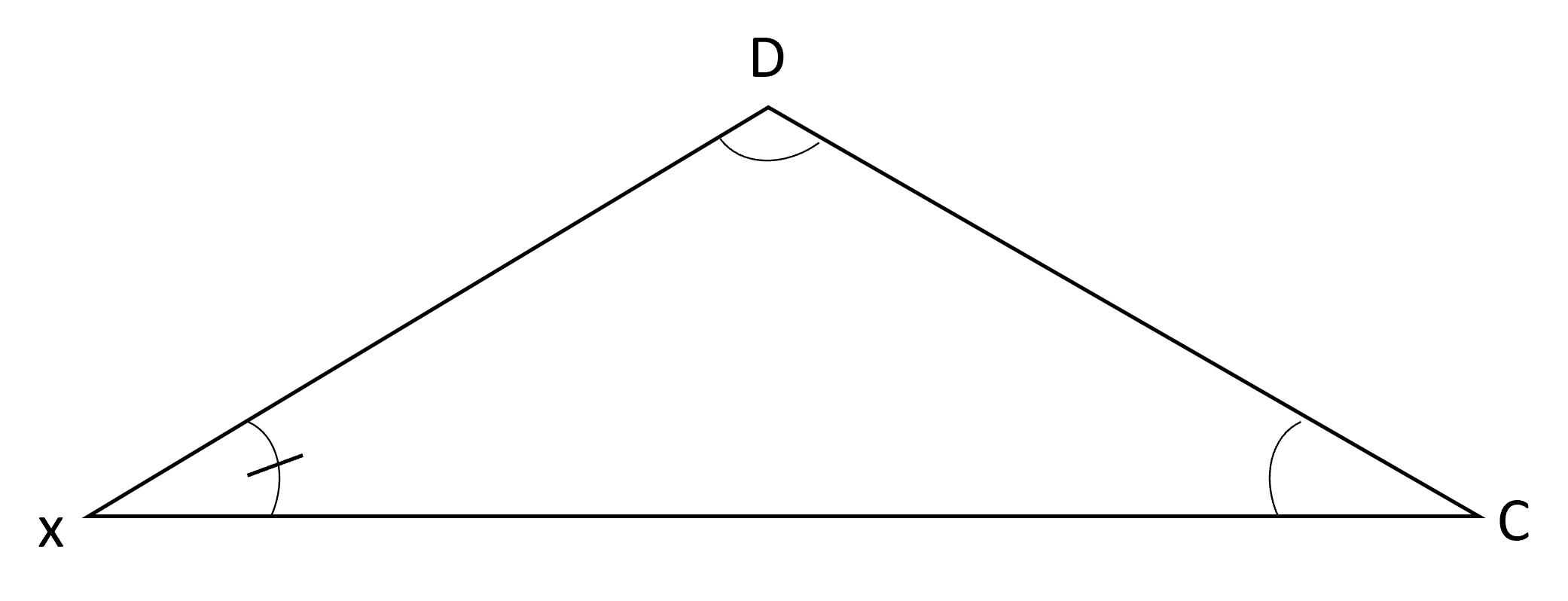
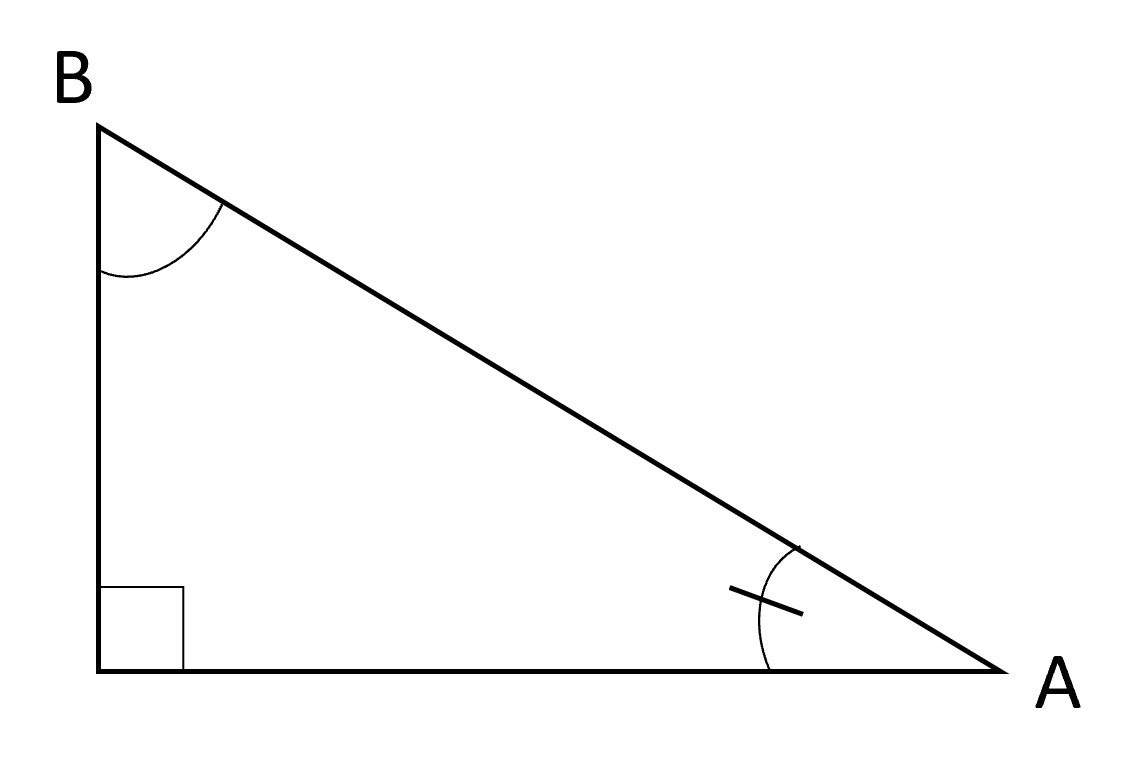
We first need to find the measure of the congruent angle in the second triangle. This is how we will connect the information between the two triangles. Remember that the sum of all angles in one triangle must equal 180º:

$$\begin{array}{rl}A+50+90& =180\\ A& =180-50-90\\ A& =40\end{array}$$

Since angles $x$ and $A$ are congruent,

$$\begin{array}{rl}x& =A\\ x& =40\end{array}$$

The measure of angle $x$ is 40º.

Congruency tests

Two triangles are not always congruent just because they share a few qualities. There are a few tests we can perform to check if two triangles are congruent. These tests are done by looking at how many of each quality the triangles have in common.

If two triangles share the same blue characteristics for a single test listed below, then they are considered congruent. If none of the tests apply to two triangles, then they are not congruent. The angles and sides listed for each test refer to the ones between the two triangles.

The lines in blue for the images below indicate where you can look to see if two triangles are congruent.

Side - side - side (SSS)

All three sides are equal:

Side - angle - side (SAS)

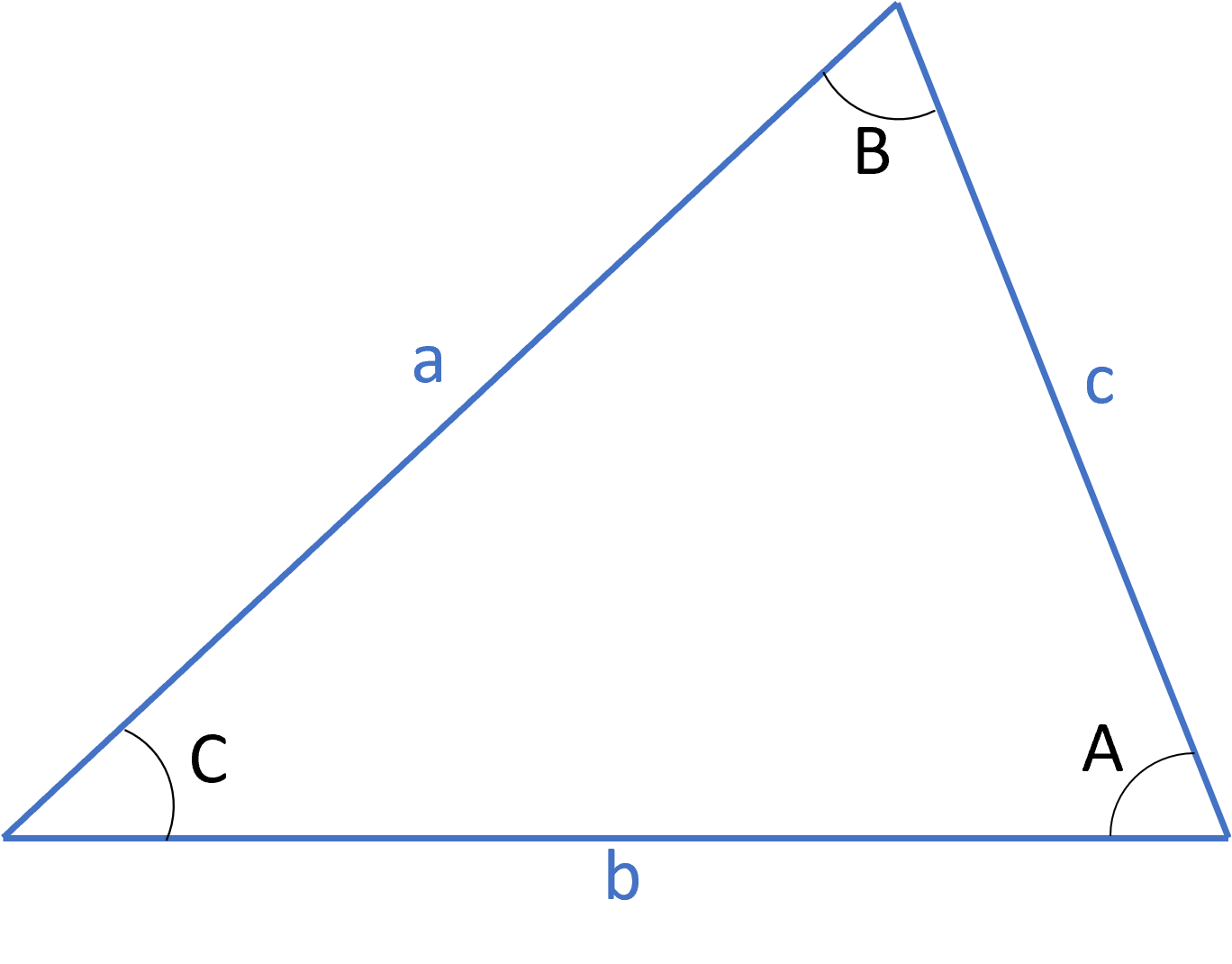
A side, angle, and another side are (in that order) equal:

Angle - side - angle (ASA)

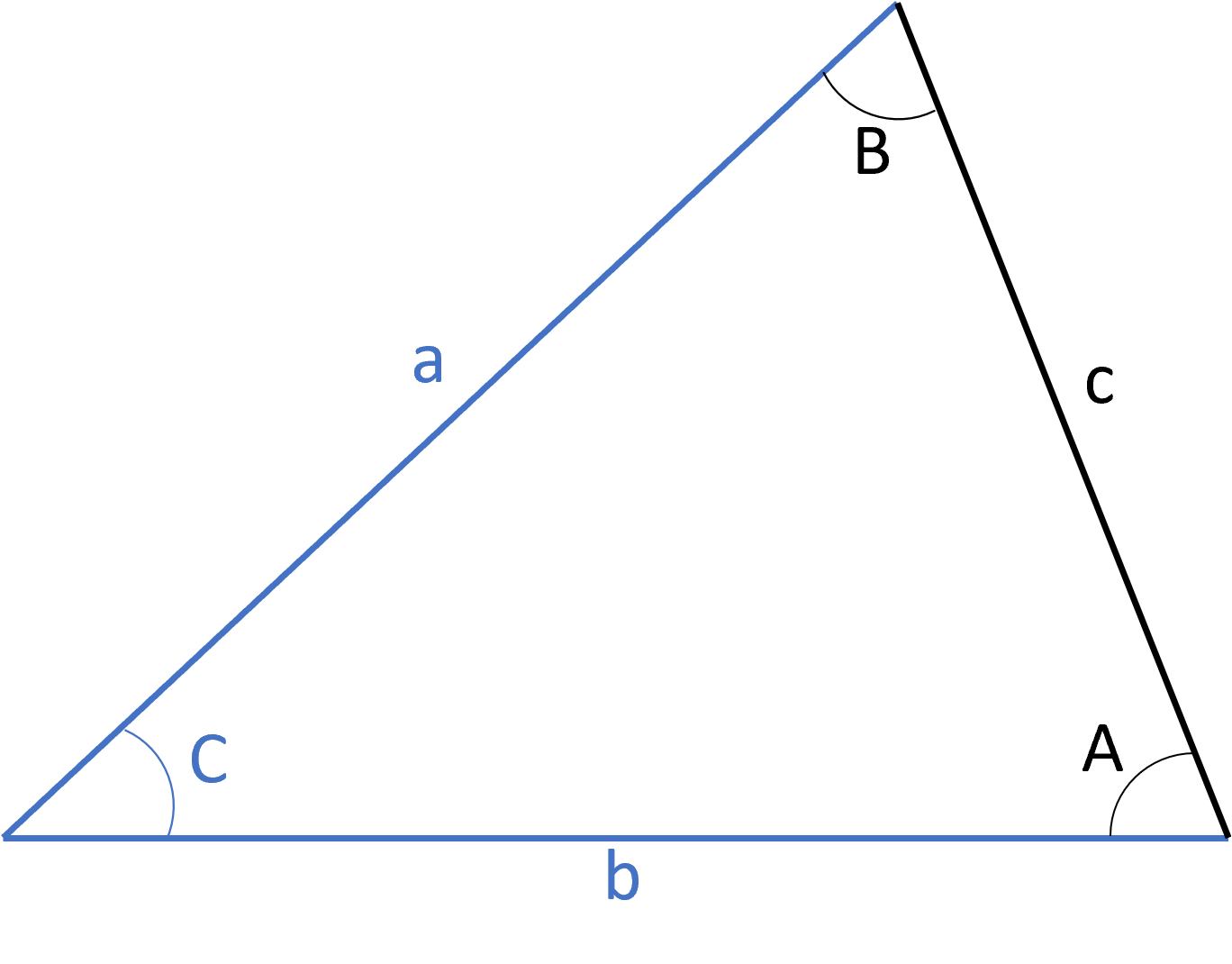
An angle, side, and another angle (in that order) are equal:

Angle - angle - side (AAS)

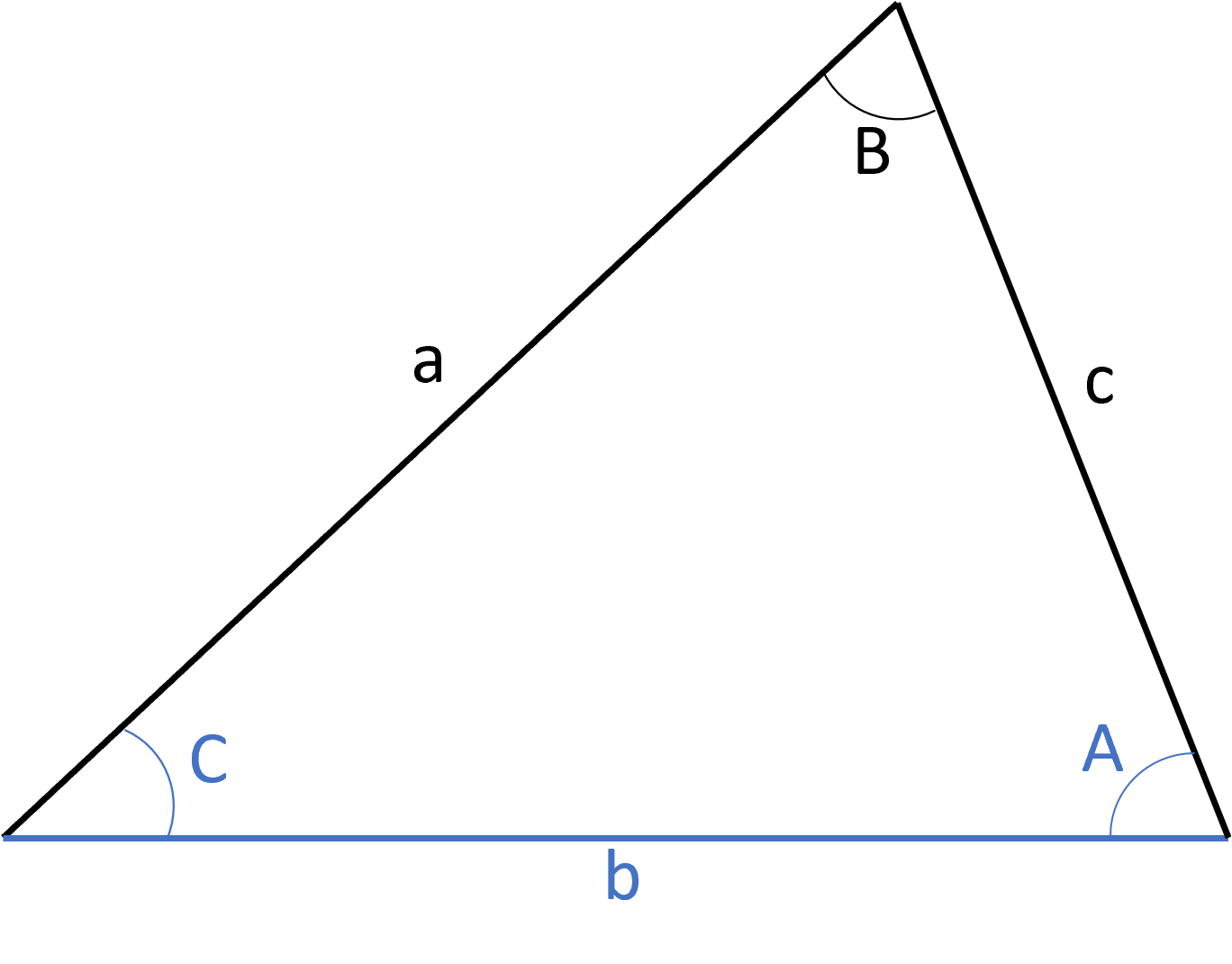
An angle, another angle, and a side (in that order) are equal:

Right angle - hypotenuse - side (RHS)

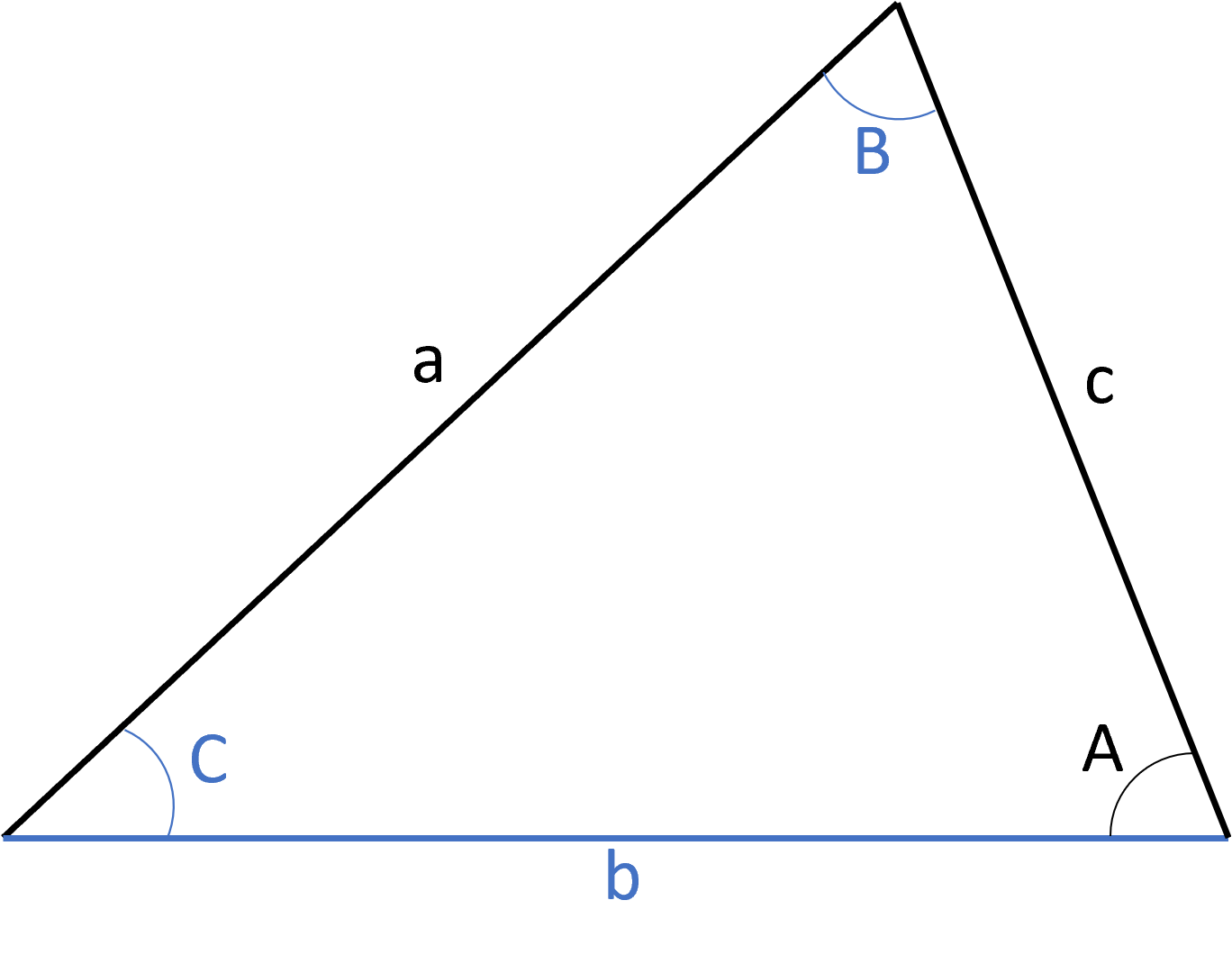
The hypotenuse, the right angle, and one side (does not matter which of the two non-hypotenuse sides) are equal:

Similarity

If two triangles are similar, it will either be stated in the problem or you will be able to tell by recognizing that the angles of the two triangles are equal.

It is useful to know that triangles are similar because this allows us to find lengths based on the proportion between the triangles. For instance, in the following example of similar triangles we can solve for $x$ just by determining the proportion of the first triangle to the second:

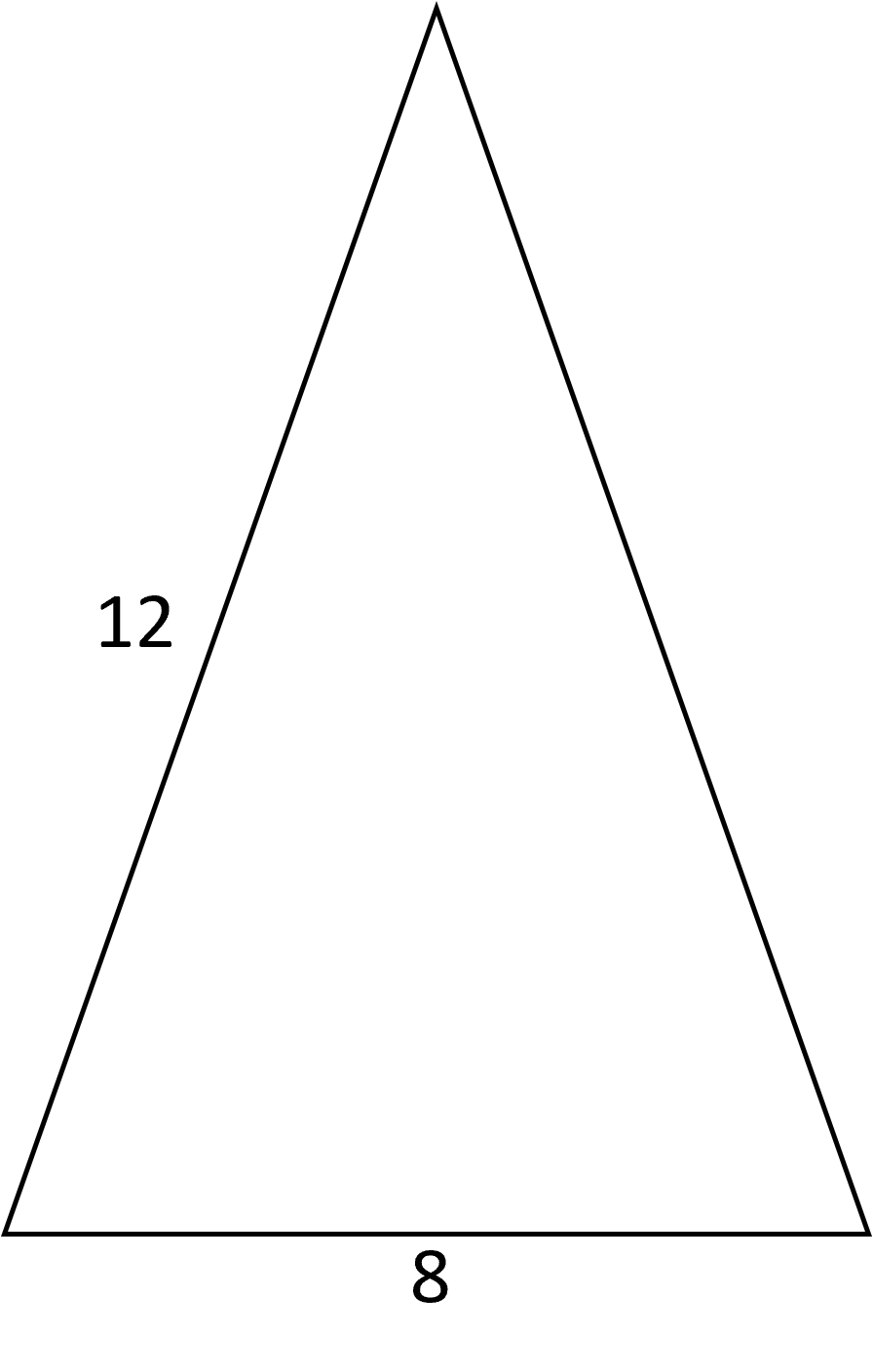
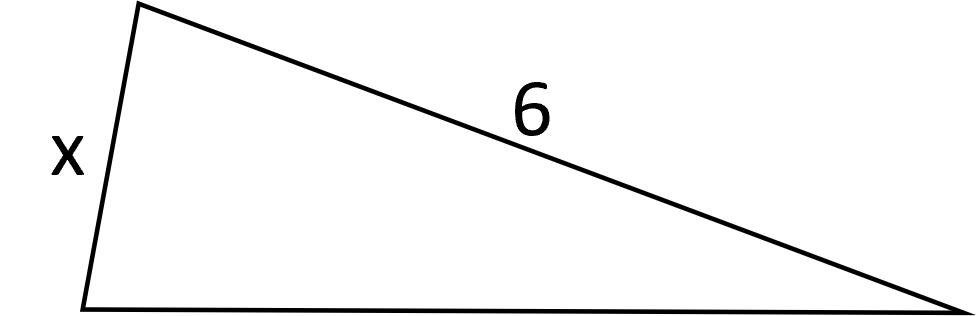
We see that the long side of the smaller triangle is half the length of the larger triangle. Because these triangles are similar, we can determine that the proportion of the larger triangle to the smaller triangle is $2:1$. We can then solve for $x$ using ratio algebra:

$$\begin{array}{rl}\frac{12}{6}& =\frac{8}{x}\\ & \\ 2& =\frac{8}{x}\\ & \\ x& =\frac{8}{2}\\ & \\ x& =4\end{array}$$

The value of the side $x$ in the above example of similar triangles is $4$.

Key points

Sum of angles. The sum of all angles in a triangle must equal 180º.

Area. The area of any triangle is equal to one-half the product of its base multiplied by its height.

Triangle Inequality Theorem. In order to form a triangle, the two smaller lengths must add together to be longer than the largest side length.

Equilateral Triangles. Triangles where all three sides and all three angles are equal to each other.

Isosceles Triangles. Triangles where two sides and two angles are equal to each other and one is not equal to the other two.

Scalene Triangles. Triangles where no sides or angles are equal to each other.

Congruency. The values of two congruent qualities are equal to each other.

Similarity. Two triangles are similar if they share the same angles but are different sizes. They are proportional to each other.