The geometry mentioned in this chapter must be memorized. Many more advanced topics of geometry and coordinate geometry involving circles will build off of the principles taught in this chapter.
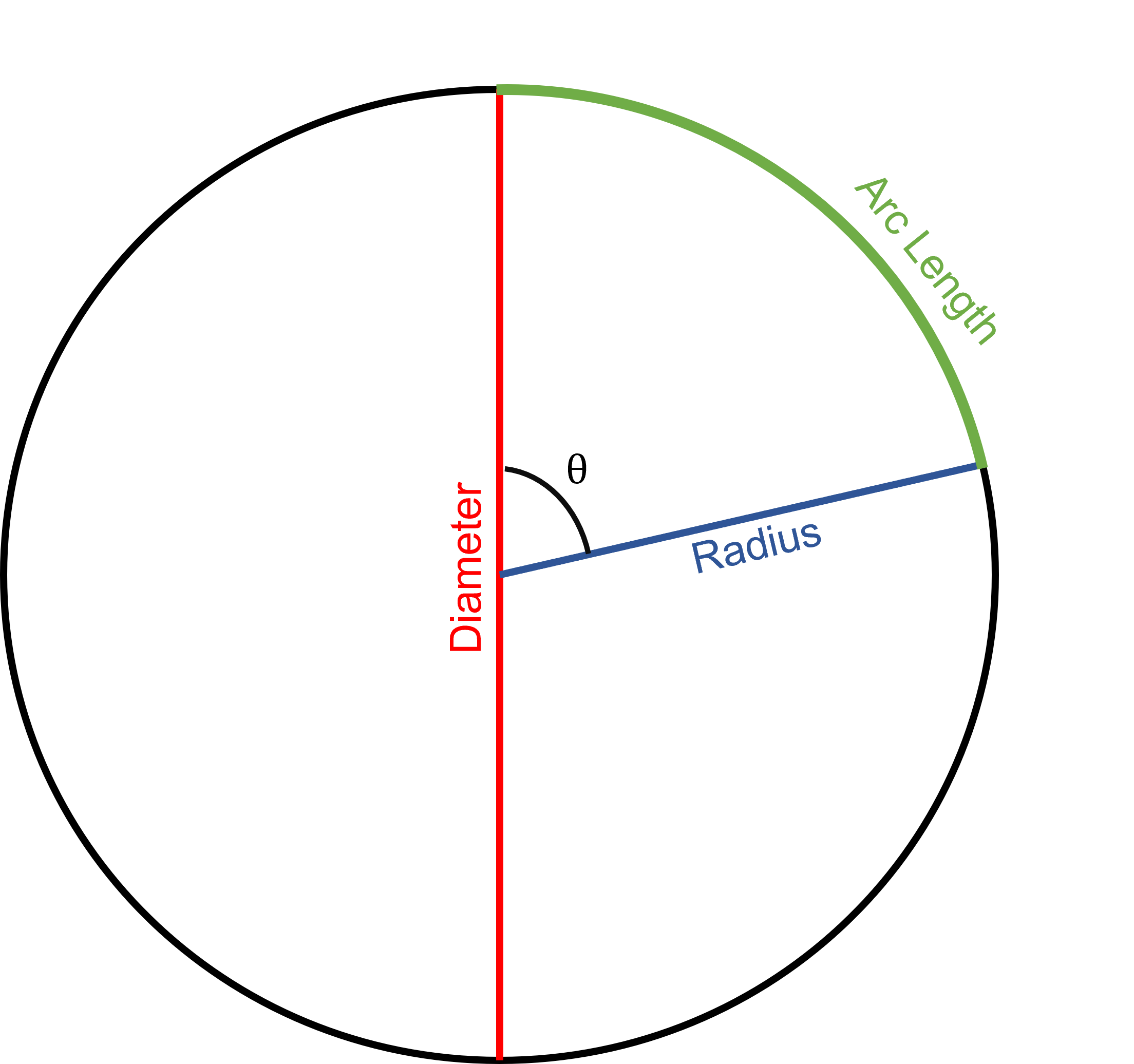
The radius () of a circle is the distance from the center of the circle to the edge of the circle. A circle is perfectly round, so the radius can touch any point on the edge and still be the same distance from the center.
The diameter () of a circle is the distance from one point on the edge of a circle, through the center, and to the opposite edge of the circle. The diameter must pass through the center. This ensures that the diameter will be the same regardless of where the points lie on the edge.
The diameter is equal to twice the radius:
Finding the area of a circle requires knowledge of the radius. In fact, the radius is all we need to find the area of a circle. The area of a circle is given by:
Where is the area, is the radius of the circle, and (pi) is a constant equal to about . Typically, there is a button on a calculator for pi.
On the test, questions may not use a number for pi but instead will include the symbol in the answer. So, if our radius were equal to and a question asked us to find the area, answers could look like either of the following:
The circumference of a circle is the distance around the outside of the circle. You can think of it as the perimeter of the circle. This may also be calculated just with the radius of a circle. It is given by the following equation:
In this equation, stands for the circumference of the circle and represents the radius of the circle.
The arc length of a circle measures the length of a portion of the circumference. Arc length is represented in equations with the variable . We find the arc length relative to an angle that we refer to as (theta). To determine the arc length relative to an angle , we use the following formula:
With in degrees (not radians):
You can easily extend this formula to be used for radians, given that a full circle in radians is .
With in radians (not degrees):
This simplifies to:
The total sum of angle measurements within a circle is 360 degrees (or radians). This means that all the angles must add up to equal 360 degrees inside the circle. If you are missing one angle, you can solve for it by remembering this rule as you would for a parallelogram.
Below is an image showing the core principles of circle geometry:
Find the circumference of a circle that has a radius of .
The circumference of the circle is equal to
Here’s another:
If a circle has a diameter of , what is its area?
First, let’s remember our formula for the area of a circle.
We must solve for the radius since we are given the diameter:
Now we can solve for the area of the circle:
The area of the circle is .
Let’s do one more focused on angles:
What is the measure of angle ?
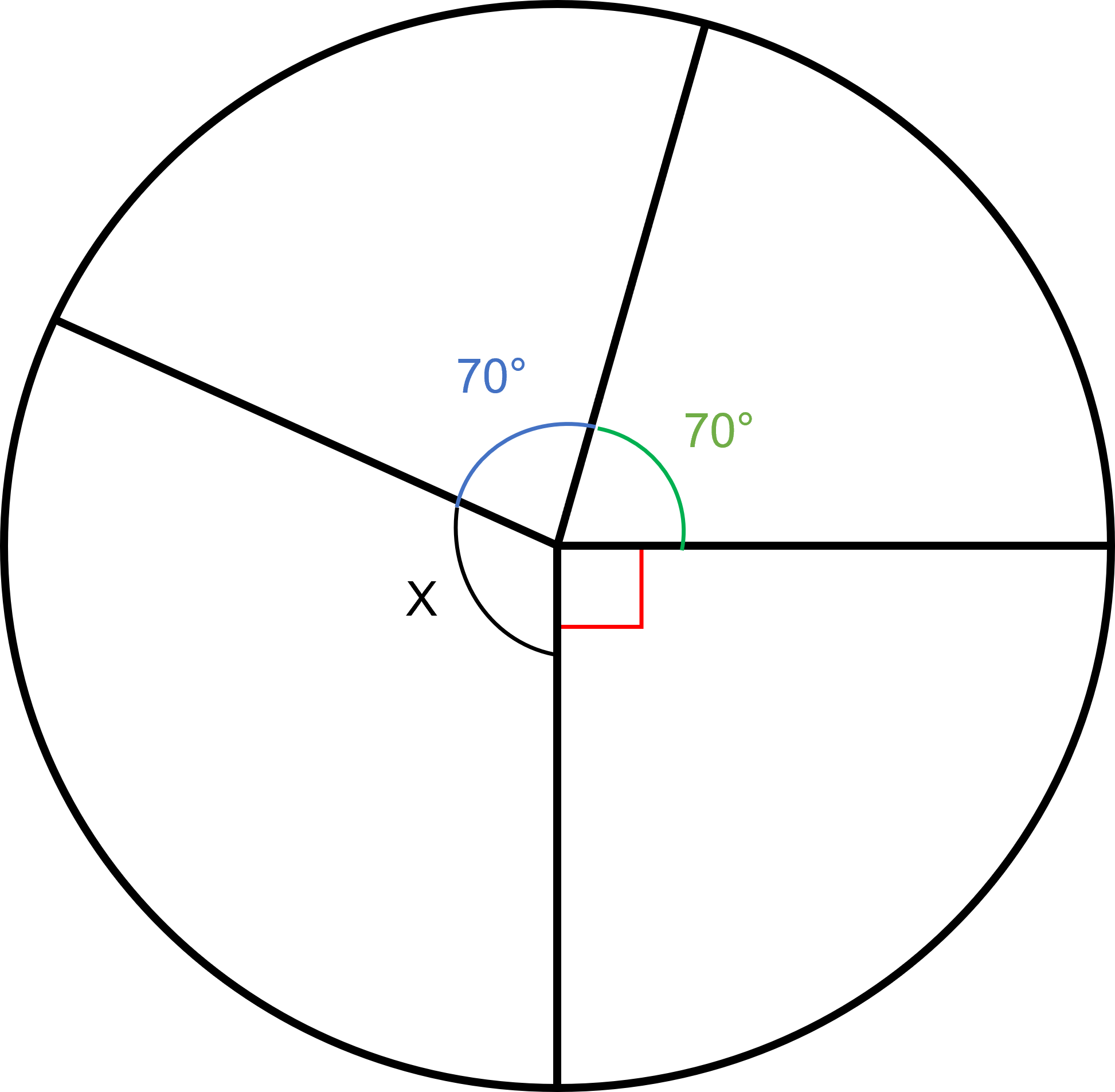
We know the sum of all the angles must equal 360 degrees and that the red angle symbolizes a right angle (90 degrees).
The measure of angle is 130 degrees.
Sign up for free to take 3 quiz questions on this topic