Solving quadratic equations

Quadratic functions are unique because they usually have two solutions (two values of the variable that make the equation true). These solutions are also called the roots or zeros of the equation.

This connects to the highest power in the equation: in a quadratic equation, the highest power of the variable is $2$, so you can expect up to two solutions. In this chapter, you’ll learn how to find both solutions by factoring and by using the quadratic formula.

Factoring

The quickest way to find the solutions to a quadratic equation is often to factor it into two sets of parentheses. However, not every quadratic can be factored nicely (or at all) using whole numbers. Refer to the chapter “Factorization of quadratics and cubics” for instructions on how to factor quadratic equations.

Once you’ve factored a quadratic into two parentheses, you find the solutions by setting each factor equal to zero and solving for $x$. Use the example $x^2+3x-4$ to see how this works.

Find the solutions to the equation:

$$x^2+3x-4$$

Factoring this equation, we get:

$$(x+4)(x-1)$$

Now set each factor equal to zero:

$$\begin{gathered} x+4=0 \\ x-1=0 \end{gathered}$$

Then solve for $x$ in each equation:

$$\begin{array}{rl}x& =-4\\ x& =1\end{array}$$

These are the solutions to the equation: $1$ and $-4$.

Something important to note is that factoring is most useful when you can factor using whole numbers. So factoring isn’t always the best option. For example, the equation below is difficult to factor using whole numbers:

$$x^2-4x+2$$

When factoring is difficult or messy, you use the quadratic formula.

Quadratic formula

The quadratic formula is a method that finds both solutions to any quadratic equation. It always works, but it usually takes longer than factoring. When factoring isn’t possible, this is the method you use.

The quadratic formula is

$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

where $a$, $b$, and $c$ are the coefficients of the quadratic equation. Notice the plus-or-minus sign ($\pm$). That symbol is what produces two solutions: you solve once using $+$ and once using $-$.

Identifying $a$, $b$, and $c$

Before using the quadratic formula, you need to identify the coefficients in standard form:

$$a{x}^2+bx+c$$

• $a$ is the number multiplying $x^2$
• $b$ is the number multiplying $x$
• $c$ is the constant term (the number with no variable)

If a term is missing, its coefficient is $0$. If a variable term is present but has no number written in front, its coefficient is $1$.

Confirm this with the following example.

What are the coefficients $a$, $b$, and $c$ of the following equation?

$$x^2-12$$

Look at the coefficient of $x^2$:

$$a=1$$

There is no $x$ term, so:

$$b=0$$

The constant term is:

$$c=-12$$

Pay close attention to the negative sign from the subtraction. Do not drop negative signs! If you lose a negative sign, you’ll get the wrong answer.

Using the quadratic formula

Now use the coefficient values from the example above:

$$\begin{array}{rl}a& =1\\ b& =0\\ c& =-12\end{array}$$

Substitute these values into the quadratic formula and simplify:

$$\begin{array}{rl}x& =\frac{-(0)\pm \sqrt{(0{)}^2-4\ast (1)\ast (-12)}}{2\ast (1)}\\ & \\ x& =\pm \frac{\sqrt{48}}{2}\end{array}$$

Now separate the $\pm$ to write both solutions:

$$\begin{array}{r}x=+\frac{\sqrt{48}}{2}\\ \\ x=-\frac{\sqrt{48}}{2}\end{array}$$

Now solve the earlier example that was not easy to factor.

Find the solutions to this equation:

$$x^2-4x+2$$

First, identify the coefficients to use in the quadratic formula. Then substitute, simplify, and solve for $x$. Remember to split the $\pm$ into both a positive and a negative solution.

Imaginary roots of a quadratic equation

It is possible to end up with a negative value inside the square root in the quadratic formula. In real numbers, square roots of negative numbers are not defined. In this situation, the solutions are imaginary roots.

For a review of imaginary numbers, see the chapter [Imaginary and complex numbers.]

Examples

Here is a reference to the quadratic formula for the examples below.

$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

Please memorize the quadratic formula, as you will be expected to know it. Sometimes singing the formula to the tune of “Pop! Goes the Weasel” is helpful. Remember, you will need to use it when factorization is not possible. However, you may choose to use it every time.

Find the roots (solutions) of the equation:

$$-2x^2-3x$$

What is the sum of the solutions to the following equation?

$$x^2-9$$

Solutions on a graph

The real solutions (roots) of a quadratic equation can often be found by looking at its graph. The idea is simple: the real solutions are the $x$-values where the curve intersects the $x$-axis.

Quadratic equations graph as parabolas. Often, the parabola crosses the $x$-axis twice, which gives two real solutions. This matches what you found earlier by solving the equation algebraically.

Look at the graph of $y=x^2-4$ below:

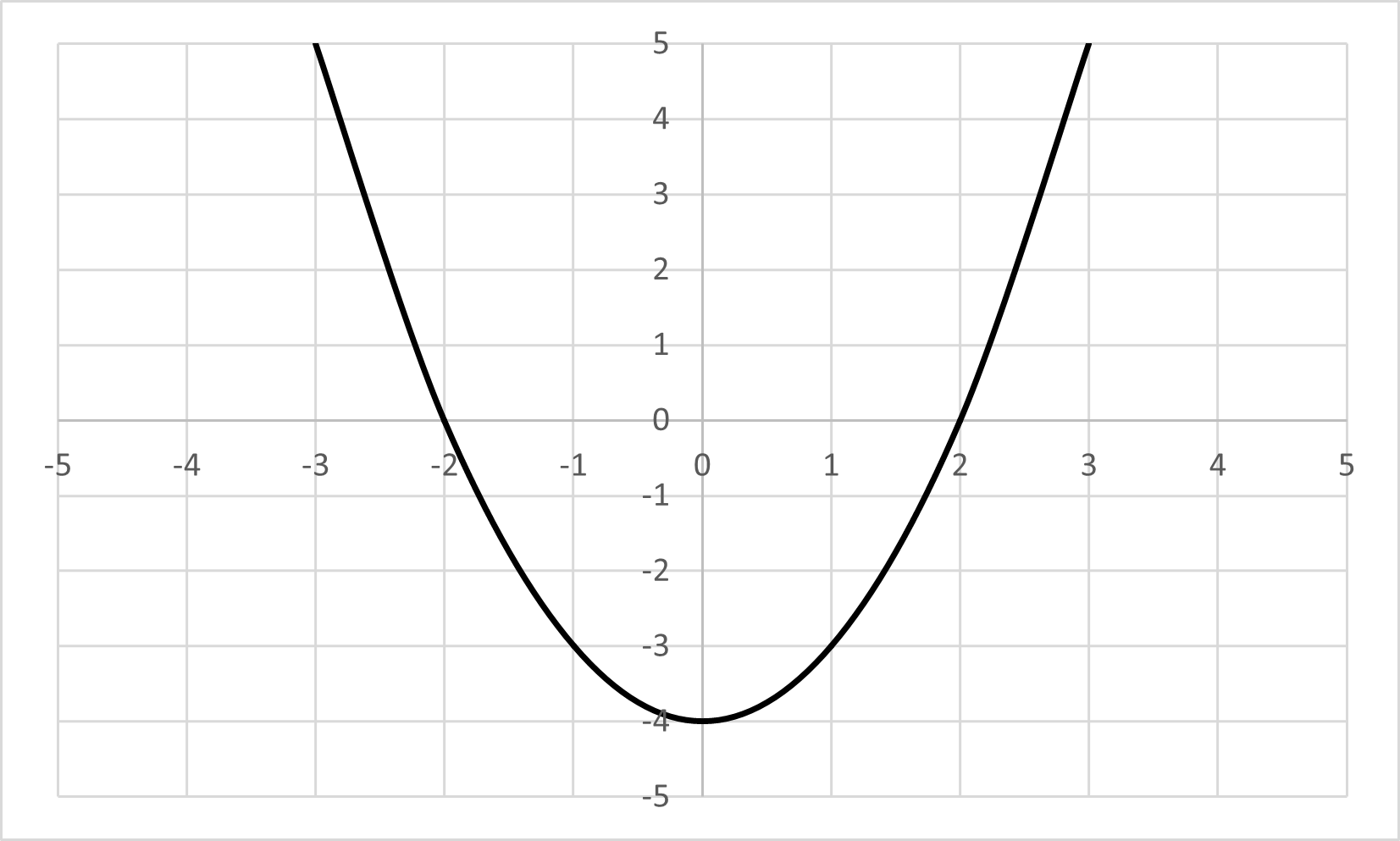
You can see that the curve intersects the $x$-axis at $x=-2$ and $x=2$. Therefore, the solutions to the quadratic equation $y=x^2-4$ are:

Sometimes, however, a parabola does not touch the $x$-axis at all. Every quadratic equation has two roots, but if the parabola doesn’t intersect the $x$-axis, the roots are imaginary. Imaginary roots can’t be read from a graph; you find them by solving with the quadratic formula. See the “Imaginary and complex numbers” chapter for more help with negative values inside the square root.

Key points

Multiple solutions. Quadratic equations have two solutions, i.e., values for $x$, that make the equation true.

Factoring. After factoring a quadratic equation, set each group of parentheses equal to zero and solve for $x$.

Quadratic formula. The quadratic formula is $x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$ where $a$, $b$, and $c$ are the coefficients of a quadratic equation.

Imaginary solutions. When you end up with a negative value within the square root of the quadratic formula, the solution will be imaginary.

Solutions on a Graph. Use the graph of a quadratic equation to find the real solutions by identifying the values at which the curve intersects the $x$-axis. The $x$-values at these points are the real solutions. If a parabola doesn’t touch the $x$-axis, it has two imaginary solutions.