Imaginary and complex numbers

Complex numbers are ordinary numbers expanded to include what are called imaginary numbers. A complex number is written $a+bi$ where $a$ and $b$ are real numbers and $i$ is an imaginary unit. All numbers are complex numbers. However, most numbers have an imaginary part equal to $0$. Think of it this way:

A complex number is written $2+3i$. A typical number is written $2+0i$ which can be simplified to just $2$. So, the number $2$ is actually a complex number where the imaginary part is equal to $0$.

In this chapter, we will explore the use of imaginary numbers in algebra.

Imaginary numbers

Imaginary unit $i$

The letter $i$ in algebra refers to the imaginary unit mentioned above. It is used to identify an imaginary term, and helps us to determine the value of the term to which it is attached. The value $i$ is defined as:

$$i=\sqrt{(-1)}$$

With this value, we can also infer the square of the unit:

$$i^2=-1$$

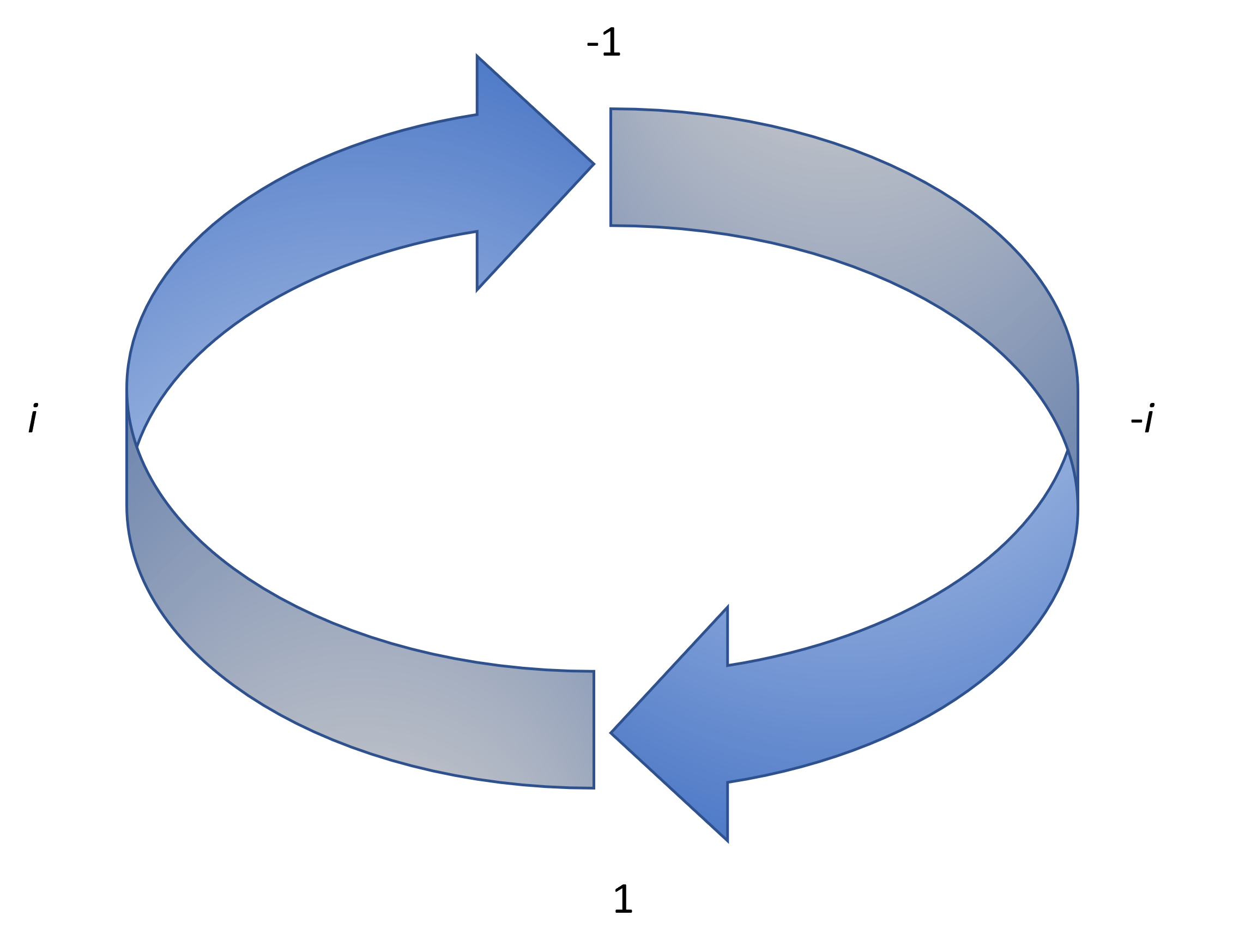
In most cases, these values will be given to you in a problem. However, it is very important to be familiar with the cycle below to feel comfortable identifying the values of $i$ raised to a given power.

Imaginary unit exponent cycle

Above, we showed the values for $i$ and $i^2$. Now, this cycle will describe how to find the value of $i$ at any exponent. It is done by following the increase in the exponent, multiplying the previous term by $i$.

Beginning with $i^2=-1$, the cycle we see is that the value of $i$ changes in the following pattern:

It can be intimidating to think about at first, but remember what exponents are: a number multiplied by itself that many times. Think about it like this:

$$i=\sqrt{(-1)}$$

so

$$i^2=i\ast i=\sqrt{(-1)}\ast \sqrt{(-1)}$$

Whenever you multiply the square root of any value times itself, the square roots go away. In this case, we’re left with $i^2=-1$.

Now $i^3$ can be written as $i^2\ast i$ from properties of exponents. We already know that $i^2=-1$ so now we multiply:

$$i^2\ast i=-1\ast i=-i$$

Again, we can rewrite $i^4$ as $i^3\ast i$ and we know that $i^3=-i$ so we can rewrite it like this:

$$i^4=i^3\ast i=-i\ast i=-i^2$$

Does that look familiar? It should! We know that $i^2=-1$ so we can rewrite our result like this:

$$i^4=-(i^2)=-(-1)=1$$

Let’s do it one final time: $i^5=i^4\ast i=1\ast i=i$. We have come full circle! And if we were to keep going, we would see this very same cycle over and over again. It may seem to you like, “Who would ever need to know this?” but trust us, it can (and almost certainly will) pop up on the ACT from time to time.

Below is a written form of the same pattern:

• $i^2=-1$
• $i^3=-i$
• $i^4=1$
• $i^5=i$
• $i^6=-1$
• $i^7=-i$

Imaginary numbers in algebra

When adding or subtracting imaginary numbers in algebra, we can treat the term “$i$” as if it were a variable. Doing this allows us to perform very simple calculations. So, we will simply add or subtract all of the numbers without an $i$ attached to them, then we will do the same for all the numbers with an $i$ attached to them, treating them as a variable. Look at the following example:

$$(2+3i)-(4-i)=-2+4i$$

Multiplication with imaginary numbers works in a similar way to how it is typically done. One important thing to note is that when you are presented with two sets of parentheses within multiplication, you must treat $i$ as a variable and FOIL the terms. Follow along below:

$$\begin{gathered} (2+3i)\ast (4-i) \\ 8-2i+12i-3i^2 \\ -3i^2+10i+8 \end{gathered}$$

You might be tempted to think we’re done, but think again! We can simplify this further. Remember how $i^2=-1$? We can use that to simplify this problem one more time!

$$\begin{gathered} -3(-1)+10i+8 \\ 3+10i+8 \\ 11+10i \end{gathered}$$

Division is a bit more complicated. In order to perform division with imaginary numbers, we have to understand what a complex conjugate is. A complex conjugate is a copy of a given complex number where the sign of the imaginary term is opposite the original number. Below is a complex number, and below that is its complex conjugate:

$$\begin{gathered} 2+3i \\ 2-3i \end{gathered}$$

We use a complex conjugate when we are performing division with a complex number composed of both imaginary and real parts. In simpler situations, we may perform familiar algebraic division. However, in our case we will learn how to divide using a complete complex number.

First, we determine the complex conjugate of the denominator of the fraction. Then, we create a new fraction composed of that complex conjugate as both the numerator and denominator. We will then multiply the original fraction by the complex conjugate divided by itself. We can do this because anything divided by itself is equal to $1$, and multiplying something by $1$ doesn’t change its value! Tricky, right? The setup will look like this:

$$\frac{(2+3i)}{(1-i)}\ast \frac{(1+i)}{(1+i)}$$

To finish the division, you will need to multiply these fractions together. FOIL the top terms and the bottom terms to get a new product fraction which will simplify to be your final answer:

$$\begin{array}{r}\frac{[(2+3i)\ast (1+i)]}{[(1-i)\ast (1+i)]}\\ \\ \frac{(2+2i+3i+3i^2)}{(1+i-i-i^2)}\\ \\ \frac{(2+2i+3i+3i^2)}{(1+i-i-i^2)}\\ \\ \frac{(3i^2+5i+2)}{(-i^2+1)}\end{array}$$

Remember that we can further simplify this answer by remembering that $i^2=-1$.

$$\begin{array}{r}\frac{(3i^2+5i+2)}{(-i^2+1)}\\ \\ \frac{(3(-1)+5i+2)}{(-(-1)+1)}\\ \\ \frac{(3(-1)+5i+2)}{(-(-1)+1)}\\ \\ \frac{(-1+5i)}{2}\end{array}$$

This is our final, simplified answer. Do you see that the denominator no longer has any $i$s in it? That’s the goal! We could split this expression into two fractions if we needed to, but here it doesn’t really help us any more.