Solving quadratic equations | Intermediate algebra | ACT Math

Quadratic functions are unique because they contain two solutions or values for the variable in the equation. They are sometimes referred to as roots or zeros of the equation. This can be related to the highest power in the equation: the highest power on a variable in a quadratic equation is $2$ , therefore there are two solutions to the equation. We will discover how to find both solutions to quadratic equations in this chapter through factoring and the use of the quadratic formula.

Factoring

The quickest way to find the solutions to a quadratic equation is by factoring it into two sets of parentheses; however, this is not possible for all quadratic equations. Refer to the chapter “Factorization of quadratics and cubics” for instructions on how to factor quadratic equations.

After finding the two sets of parentheses from factoring a quadratic equation, all we have to do to find the solutions is put each set equal to zero and solve for $x$ . Use the following example of the equation $x^{2} + 3 x - 4$ to explore this.

Find the solutions to the equation:

$x^{2} + 3 x - 4$

Factoring this equation, we get:

$(x + 4) (x - 1)$

Now, we will set each group of parentheses equal to zero:

$x + 4 = 0 x - 1 = 0$

Then, solve for $x$ in both equations:

$x x = - 4 = 1$

These are our solutions to the equation: $1$ and $- 4$ .

Something important to note is that factoring is most useful to us when we can factor the equation using whole numbers. So, factoring is not always the best option. In the following example, you will see that we are unable to factor the equation using whole numbers.

$x^{2} - 4 x + 2$

When factoring is difficult or messy, we use the quadratic formula.

Quadratic formula

The quadratic formula is a formula used to find both solutions to any quadratic equation. This equation will always work for any quadratic equation, but it takes longer to do than factoring. In cases where factoring is not possible, this is what you need to use to find the solutions.

The quadratic formula is

$x = \frac{- b \pm b ^{2} - 4 a c}{2 a}$

where $a$ , $b$ , and $c$ are the coefficients of the equation used. Notice the plus-or-minus sign. This is where our two solutions come from in the equation. The equation will be solved using a plus sign, and then solved again using a minus sign. We will figure out how to do this later.

Let’s first get comfortable identifying the coefficients of a quadratic equation. The coefficient $a$ is the number attached to the front of $x^{2}$ , $b$ is the number attached to the front of $x$ , and $c$ is the third number in the equation with no variable attached to it. If any term is missing in the equation, the coefficient is equal to $0$ . If a variable is present but there is no number attached to it, the coefficient is equal to $1$ . Confirm this with the following example.

What are the coefficients $a$ , $b$ , and $c$ of the following equation?

$x^{2} - 12$

Look at the number attached to the first term, which should have $x^{2}$ :

$a = 1$

Now, the next term should have $x$ but there is no $x$ to the first power. So,

$b = 0$

Lastly, look at the third term, which should be a number with no $x$ :

$c = - 12$

Pay close attention to the negative sign that came from the subtraction in the equation. Do not drop negative signs! You will get the wrong answer if you forget the negative signs.

Now, we can try using the full quadratic formula. We will use the coefficient values from the above example:

$a b c = 1 = 0 = - 12$

We will simply substitute these values in for their corresponding letters in the quadratic formula and simplify the equation with our new values:

$x x = \frac{- ( 0 ) \pm ( 0 ) ^{2} - 4 * ( 1 ) * ( - 12 )}{2 * ( 1 )} = \pm \frac{48}{2}$

At this point, we have our answers. What we need to do now is separate the plus-or-minus sign to form both of our solutions $\frac{48}{2}$ and $- \frac{48}{2}$ :

$x = + \frac{48}{2} x = - \frac{48}{2}$

Now that we know how to use the quadratic formula, let’s solve the example from earlier that we were not able to factor.

Find the solutions to this equation:

$x^{2} - 4 x + 2$

First, find the coefficients to put into the quadratic equation. Then, simplify the equation and solve for $x$ . Remember to separate the plus-or-minus sign into both a positive and negative solution!

(spoiler)

Quadratic formula:

$x = \frac{- b \pm b ^{2} - 4 * a * c}{2 a}$

Coefficients: $a = 1, b = - 4, c = 2$

New quadratic formula:

$x = \frac{- ( - 4 ) \pm ( - 4 ) ^{2} - 4 * ( 1 ) * ( 2 )}{2 ( 1 )}$

Simplified formula:

$x x = \frac{4 \pm 16 - 8}{2} = \frac{4 \pm 8}{2}$

Let’s go ahead and split up the plus-or-minus sign to get our solutions.

$x = \frac{4 + 8}{2} x = \frac{4 - 8}{2}$

This is sufficient as an answer, but you may be asked to find the exact values by putting the expressions into your calculator and getting a decimal. Doing this, we get that $x = 3.41$ and $x = 0.59$

Imaginary roots of a quadratic equation

It is possible to end up with a negative value inside the square root of the quadratic formula. Normally, you consider square roots of negative numbers to be invalid. However, while solving the quadratic formula you must recognize them as imaginary roots.

For a review of imaginary numbers, see the chapter [Imaginary and complex numbers.]

Examples

Here is a reference to the quadratic formula for the examples below.

$x = \frac{- b \pm b ^{2} - 4 a c}{2 a}$

Please memorize the quadratic formula, as you will be expected to know it. Sometimes singing the formula to the tune of “Pop! Goes the Weasel” is helpful. Give it a shot! Remember, you will need to use it when factorization is not possible. However, you may choose to use it every time.

Find the roots (solutions) of the equation:

$- 2 x^{2} - 3 x$

(spoiler)

Coefficients: $a = - 2, b = - 3, c = 0$

Quadratic formula with coefficients:

$x = \frac{- ( - 3 ) \pm - 3 ^{2} - 4 * ( - 2 ) * ( 0 )}{2 ( - 2 )}$

Simplified formula:

$x = \frac{6 \pm 9 + 0}{- 4}$

Split plus-or-minus sign:

$x = \frac{6 + 9}{- 4} x = \frac{6 - 9}{- 4}$

Simplify for $x$ :

$x = - \frac{9}{4} x = - \frac{3}{4}$

The roots of this equation are $- \frac{9}{4}$ and $- \frac{3}{4}$ .

What is the sum of the solutions to the following equation?

$x^{2} - 9$

(spoiler)

Factored equation: $(x + 3) (x - 3)$

Parentheses set equal to $0$ :

$x + 3 = 0 x - 3 = 0$

Solve for $x$ :

$x x = - 3 = 3$

The question asks for the sum of the two solutions:

$x = 3 + (- 3) = 0$

The sum of the two solutions is $0$ .

Solutions on a graph

The real solutions, or roots, to a quadratic equation can most times be found with just a graphed curve. It is actually fairly simple: the real solutions are the $x$ -values where the curve intersects the $x$ -axis. Quadratic equations always make parabolas when graphed. Usually, there are two intersections through the $x$ -axis, so there are two real solutions. This is just as we did above with the direct equations. Take a look at the graph of $y = x^{2} - 4$ below for a visualization:

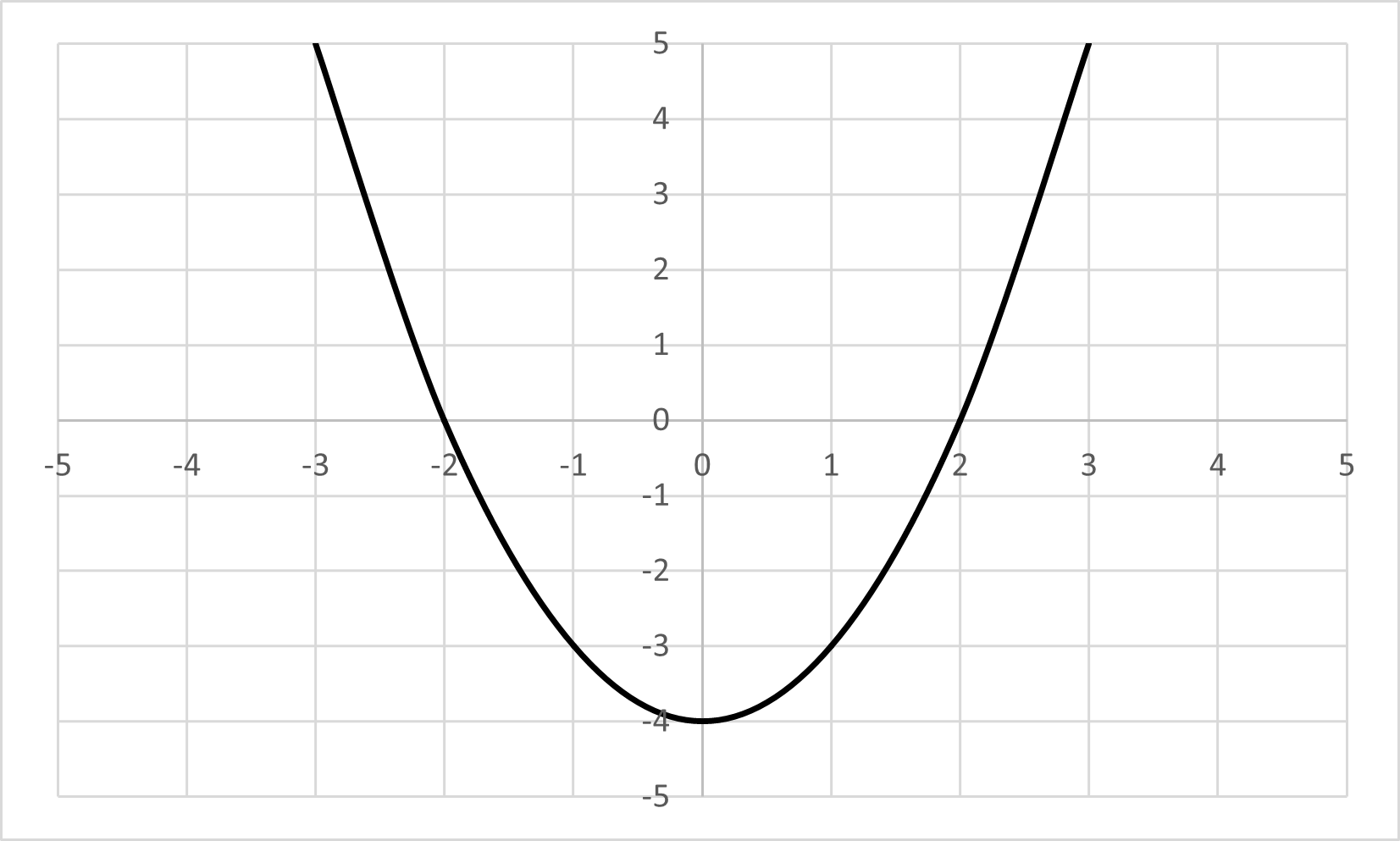
$Graph of a quadratic equation$

You can see that the curve intersects the $x$ -axis at the values $x = - 2$ and $x = 2$ . Therefore, what are the solutions to the quadratic equation $y = x^{2} - 4$ ?

(spoiler)

$x x = - 2 = 2$

Sometimes, however, we can have a parabola that does not touch the $x$ -axis at all! Every quadratic equation has two roots, or solutions, but when the parabola does not touch the $x$ -axis, these roots are called imaginary, and they can’t be found by looking at a graph. You can only find imaginary roots by solving the equation using the quadratic formula. See the “Imaginary and complex numbers” chapter for more help on how to handle the negative value inside the square root when using the quadratic formula.

Key points

Multiple solutions. Quadratic equations have two solutions, i.e., values for $x$ , that make the equation true.

Factoring. After factoring a quadratic equation, set each group of parentheses equal to zero and solve for $x$ .

Quadratic formula. The quadratic formula is $x = \frac{- b \pm b ^{2} - 4 a c}{2 a}$ where $a$ , $b$ , and $c$ are the coefficients of a quadratic equation.

Imaginary solutions. When you end up with a negative value within the square root of the quadratic formula, the solution will be imaginary.

Solutions on a Graph. Use the graph of a quadratic equation to find the real solutions by identifying the values at which the curve intersects the $x$ -axis. The $x$ -values at these points are the real solutions. If a parabola doesn’t touch the $x$ -axis, it has two imaginary solutions.

Factoring

Find the solutions to the equation:

$x^{2} + 3 x - 4$

Factoring this equation, we get:

$(x + 4) (x - 1)$

Now, we will set each group of parentheses equal to zero:

$x + 4 = 0 x - 1 = 0$

Then, solve for $x$ in both equations:

$x x = - 4 = 1$

These are our solutions to the equation: $1$ and $- 4$ .

$x^{2} - 4 x + 2$

When factoring is difficult or messy, we use the quadratic formula.

Quadratic formula

The quadratic formula is

$x = \frac{- b \pm b ^{2} - 4 a c}{2 a}$

What are the coefficients $a$ , $b$ , and $c$ of the following equation?

$x^{2} - 12$

Look at the number attached to the first term, which should have $x^{2}$ :

$a = 1$

Now, the next term should have $x$ but there is no $x$ to the first power. So,

$b = 0$

Lastly, look at the third term, which should be a number with no $x$ :

$c = - 12$

Pay close attention to the negative sign that came from the subtraction in the equation. Do not drop negative signs! You will get the wrong answer if you forget the negative signs.

Now, we can try using the full quadratic formula. We will use the coefficient values from the above example:

$a b c = 1 = 0 = - 12$

We will simply substitute these values in for their corresponding letters in the quadratic formula and simplify the equation with our new values:

$x x = \frac{- ( 0 ) \pm ( 0 ) ^{2} - 4 * ( 1 ) * ( - 12 )}{2 * ( 1 )} = \pm \frac{48}{2}$

At this point, we have our answers. What we need to do now is separate the plus-or-minus sign to form both of our solutions $\frac{48}{2}$ and $- \frac{48}{2}$ :

$x = + \frac{48}{2} x = - \frac{48}{2}$

Now that we know how to use the quadratic formula, let’s solve the example from earlier that we were not able to factor.

Find the solutions to this equation:

$x^{2} - 4 x + 2$

(spoiler)

Quadratic formula:

$x = \frac{- b \pm b ^{2} - 4 * a * c}{2 a}$

Coefficients: $a = 1, b = - 4, c = 2$

New quadratic formula:

$x = \frac{- ( - 4 ) \pm ( - 4 ) ^{2} - 4 * ( 1 ) * ( 2 )}{2 ( 1 )}$

Simplified formula:

$x x = \frac{4 \pm 16 - 8}{2} = \frac{4 \pm 8}{2}$

Let’s go ahead and split up the plus-or-minus sign to get our solutions.

$x = \frac{4 + 8}{2} x = \frac{4 - 8}{2}$

This is sufficient as an answer, but you may be asked to find the exact values by putting the expressions into your calculator and getting a decimal. Doing this, we get that $x = 3.41$ and $x = 0.59$

Imaginary roots of a quadratic equation

For a review of imaginary numbers, see the chapter [Imaginary and complex numbers.]

Examples

Here is a reference to the quadratic formula for the examples below.

$x = \frac{- b \pm b ^{2} - 4 a c}{2 a}$

Find the roots (solutions) of the equation:

$- 2 x^{2} - 3 x$

(spoiler)

Coefficients: $a = - 2, b = - 3, c = 0$

Quadratic formula with coefficients:

$x = \frac{- ( - 3 ) \pm - 3 ^{2} - 4 * ( - 2 ) * ( 0 )}{2 ( - 2 )}$

Simplified formula:

$x = \frac{6 \pm 9 + 0}{- 4}$

Split plus-or-minus sign:

$x = \frac{6 + 9}{- 4} x = \frac{6 - 9}{- 4}$

Simplify for $x$ :

$x = - \frac{9}{4} x = - \frac{3}{4}$

The roots of this equation are $- \frac{9}{4}$ and $- \frac{3}{4}$ .

What is the sum of the solutions to the following equation?

$x^{2} - 9$

(spoiler)

Factored equation: $(x + 3) (x - 3)$

Parentheses set equal to $0$ :

$x + 3 = 0 x - 3 = 0$

Solve for $x$ :

$x x = - 3 = 3$

The question asks for the sum of the two solutions:

$x = 3 + (- 3) = 0$

The sum of the two solutions is $0$ .

Solutions on a graph

$Graph of a quadratic equation$

You can see that the curve intersects the $x$ -axis at the values $x = - 2$ and $x = 2$ . Therefore, what are the solutions to the quadratic equation $y = x^{2} - 4$ ?

(spoiler)

$x x = - 2 = 2$

Key points

Multiple solutions. Quadratic equations have two solutions, i.e., values for $x$ , that make the equation true.

Factoring. After factoring a quadratic equation, set each group of parentheses equal to zero and solve for $x$ .

Quadratic formula. The quadratic formula is $x = \frac{- b \pm b ^{2} - 4 a c}{2 a}$ where $a$ , $b$ , and $c$ are the coefficients of a quadratic equation.

Imaginary solutions. When you end up with a negative value within the square root of the quadratic formula, the solution will be imaginary.