Prime factorization is a way to factor out a single large number into a bunch of smaller prime numbers. In other words, when you perform prime factorization on a number you will be left with a series of prime numbers whose product, when multiplied together, is the original number.
For instance, the prime factorization of is . You can see that each of the numbers is a prime number and their product is .
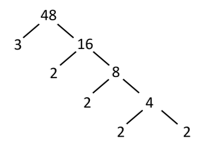
The most consistent way to perform prime factorization is by using a factor tree as detailed in the chapter “GCF/LCM.” However, we will detail it briefly in this chapter as well. The key concept is beginning with a large number and slowly breaking it down by factoring out one smaller number at a time until all the branches are reduced to prime numbers. The following factor trees provide the prime factorization for the numbers and .
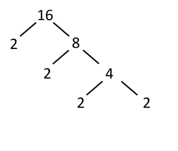
The prime factorization of is .
The prime factorization of is
Prime factorization is a useful method of factoring because, as you can see above, the final numbers of each branch cannot be factored any further. This is the most broken-down mathematical description of the larger number. Most importantly, it does show up occasionally on the ACT!
Sign up for free to take 3 quiz questions on this topic