Vectors

Vectors are lines that have a size and point in a specific direction. The size of a vector is called its magnitude. In this chapter we will review an introduction to vectors, namely their notation and how to add or subtract them from one another.

Vector notation

Vectors are described using different variables from the usual ones we have seen. They are described using $i$ in place of $x$ and $j$ instead of $y$. We also use the letters $i$ and $j$ in a mathematical form, instead of a usual coordinate point.

$i$ measures the distance that the vector travels in the $x$ direction, and $j$ measures the distance that the vector travels in the $y$ direction.

So, for a vector that begins at $(0,0)$ and ends at $(1,2)$, we would express it in vector notation as $i+2j$. This expression tells us that the vector moves one unit to the right ($i$) and two units up ($2j$).

Try turning the following examples into vector notation:

A vector begins at $(0,0)$ and ends at $(-2,3)$

A vector begins at $(3,0)$ and ends at $(0,0)$

A vector begins at $(5,2)$ and ends at $(7,7)$

Vector addition

Adding by algebra

When presented with multiple vectors, we add them by treating $i$ and $j$ as variables and combining their notations together into a single expression. Terms with $i$ will add together, and terms with $j$ will add together. Look at the following example:

What is the sum of the following vectors?

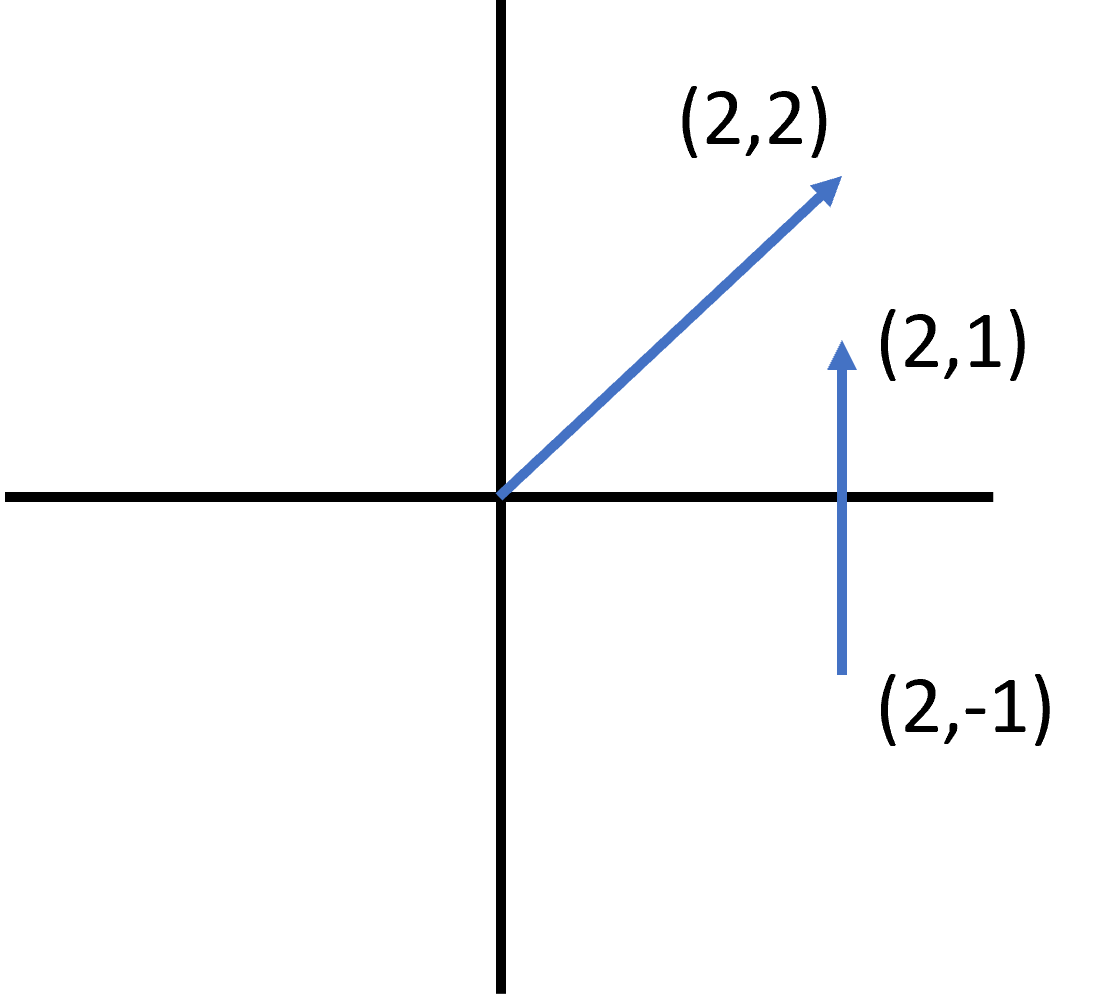
The first vector goes from $(0,0)$ to $(2,2)$. This is an increase in $x$ of $2$ and an increase in $y$ of $2$. In vector notation, we write $2i+2j$.

The second vector goes from $(2,-1)$ to $(2,1)$. This has no change in $x$, but it has an increase in $y$ of $2$. In vector notation, we write $2j$. There is no $i$ because the $x$ position does not move.

To find the sum, we add the like components:

$$\begin{array}{rl}& =2i+2j+0i+2j\\ & =2i+4j\end{array}$$

So, the sum of the two vectors is described by the expression $2i+4j$.

Adding by visualization

To see the vector that would result from adding two vectors together, we simply connect the vectors from head to tail. Then, we draw a new vector from the starting point to the new ending point. This vector is the sum of the original vectors:

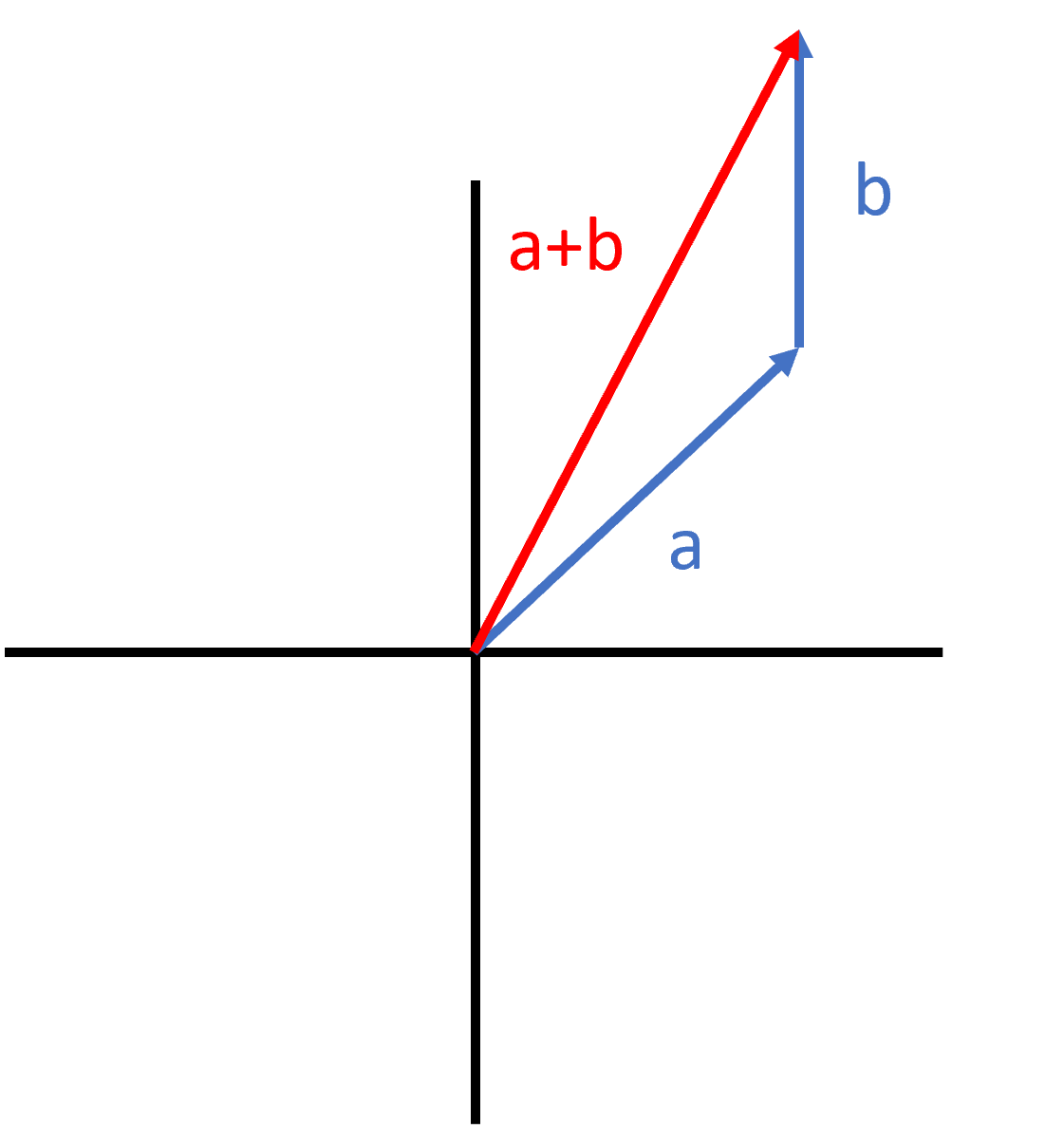
If $a$ and $b$ are the same vectors that we used in the previous example, the new vector goes from $(0,0)$ to $(2.4)$ giving us a vector $2i+4j$. This is the same result we achieved by adding the equations together.

Vector subtraction

Subtracting by algebra

Subtracting vectors is very similar to addition. We take the terms from the first vector notation and subtract the terms from the second. $i$ terms will be subtracted from each other, and so will $j$ terms:

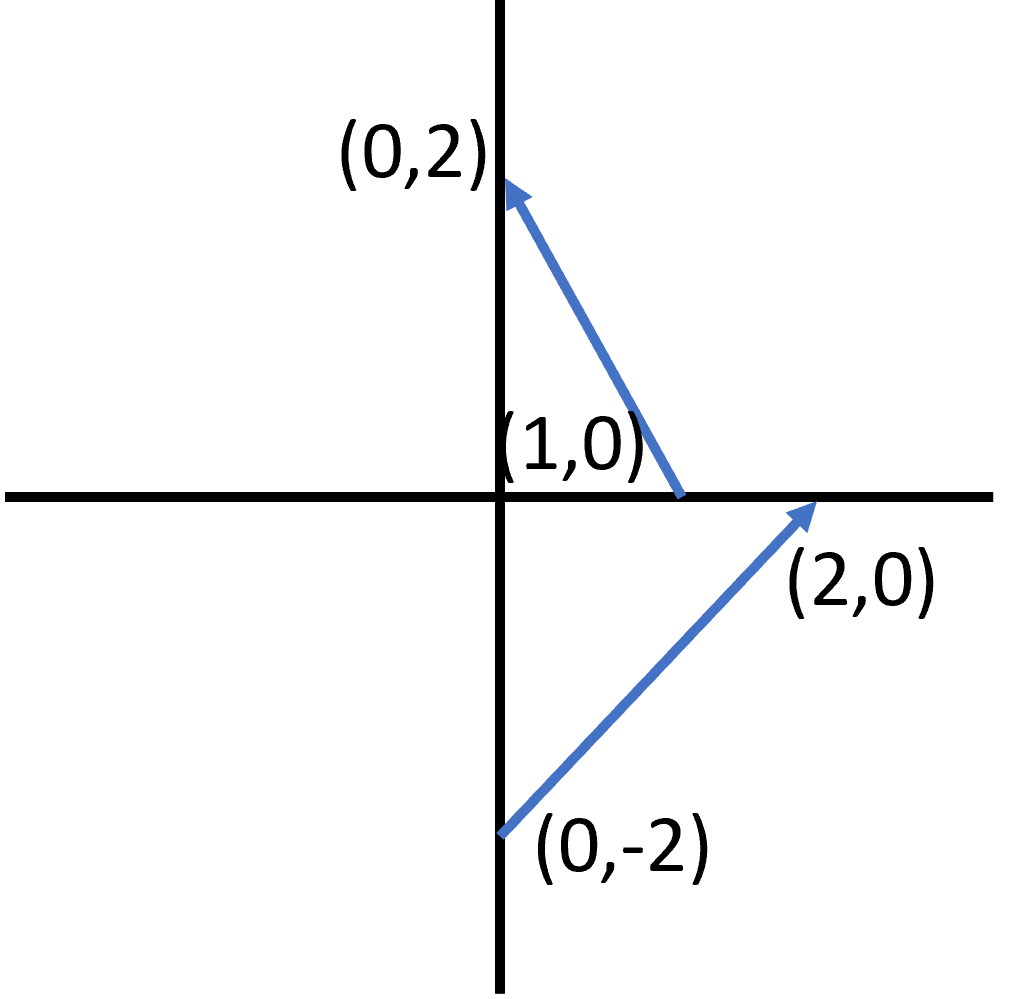
The first vector goes from $(1,0)$ to $(0,2)$. This is a decrease in $x$ of $1$ and an increase in $y$ of $2$. In vector notation, we write $-i+2j$.

The second vector goes from $(0,-2)$ to $(2,0)$. This has an increase in $x$ of $2$ and an increase in $y$ of $2$. In vector notation, we write $2i+2j$.

To find the difference, we subtract the like components of the second vector from the first:

$$\begin{array}{rl}& =-i+2j-(2i+2j)\\ & =-3i\end{array}$$

So, the difference of the two vectors is described as $-3i$.

Subtracting by visualization

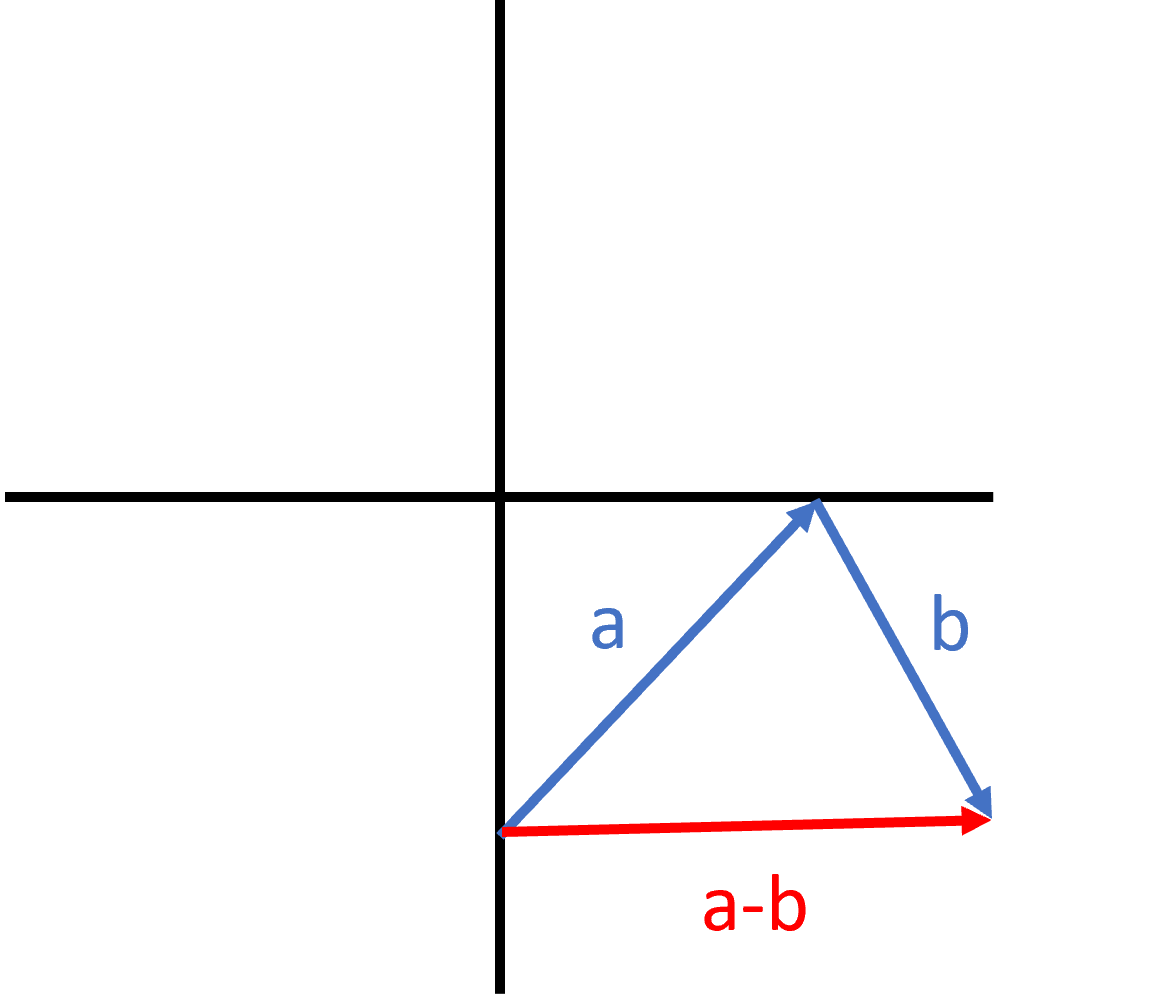
To find the vector that results from subtracting one vector from another, we will flip the vector that is being subtracted, then connect it from head to tail as above. Now, we draw a new vector connecting the starting point to the new ending point. This vector is the difference of the original vectors: