Vertex form equation (a, h, and k)

A quadratic equation may be expressed in a different way that highlights the location of the vertex. Remember, the vertex is the folding point of a parabola or absolute value graph which makes a maximum or minimum value.

This new form of writing a quadratic equation is known as the vertex form of the quadratic equation:

$$y=a(x-h{)}^2+k$$

Or the absolute value equation:

$$y=a|x-h|+k$$

In this equation, $h$ represents the horizontal shift, or how far the graph moves horizontally from $x=0$, and $k$ represents the vertical shift, or how far the graph moves vertically from $y=0$, and $a$ is a constant that tells us how much the graph stretches or shrinks vertically and if the $a$ is negative, it tells us that the function is reflected over the $x$-axis, or in other words, it’s upside-down.

This form of the equation is useful because when we put $h$ and $k$ together, the coordinate point $(h,k)$ tells us the point of the vertex. It also allows us to envision what the graph will look like compared to the parent function (e.g., $y=x^2$ or $y=|x|$) without actually graphing it.

Find the equation from a graph—quadratic

You may be given a graph and be asked to find the equation that describes it. In this case, you would need to locate the vertex, and its coordinates in the vertex form of the quadratic equation.

We will find the equation associated with the following graph:

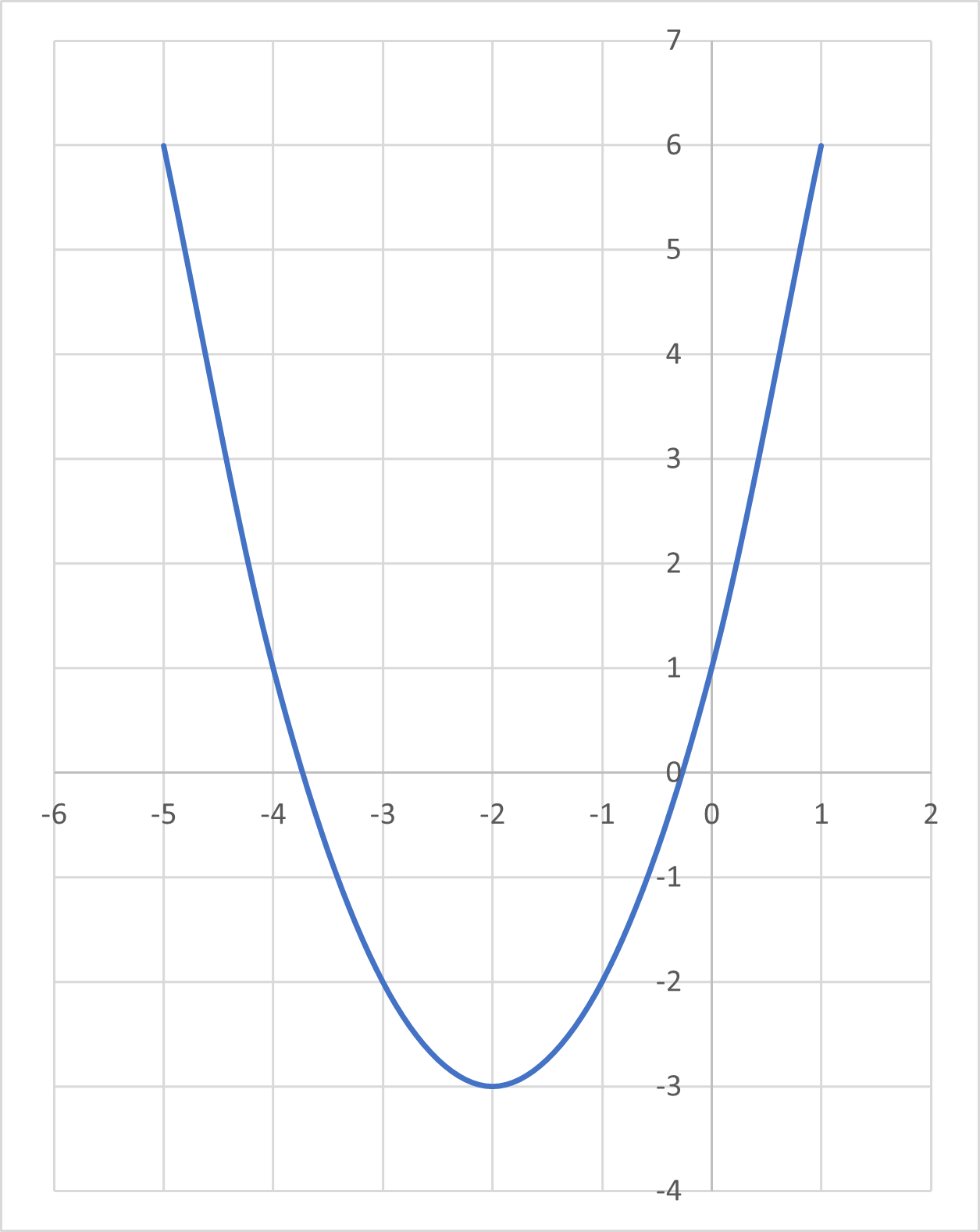
Start with the vertex. The vertex is at point $(-2,-3)$. So:

$$\begin{gathered} h=-2 \\ k=-3 \end{gathered}$$

Now, we can put these values into the formula for the vertex form of a quadratic equation:

$$\begin{array}{rl}y& =a(x-h{)}^2+k\\ y& =a(x+2{)}^2-3\end{array}$$

To find the value of $a$, we can plug in any point of the graph to see if the y value corresponds with the $x$ value. For instance, if we plug in $x=0$ into the graph, we get $y=1$. So, let’s find the value for $a$ which makes this true:

$$\begin{array}{rl}y& =a(0+2{)}^2-3\\ 1& =a(2{)}^2-3\\ 1& =4a-3\\ 4& =4a\\ a& =1\end{array}$$

Now that we know that $a=1$, we can make our final equation:

$$y=(x+2{)}^2-3$$

So, we find the vertex, form the equation, find the value of $a$, and make the final equation. These are the steps we follow to find the equation associated with any quadratic graph.

Find the equation from a graph—absolute value

Following a similar manner as above, we will find the equation associated with the following absolute value graph:

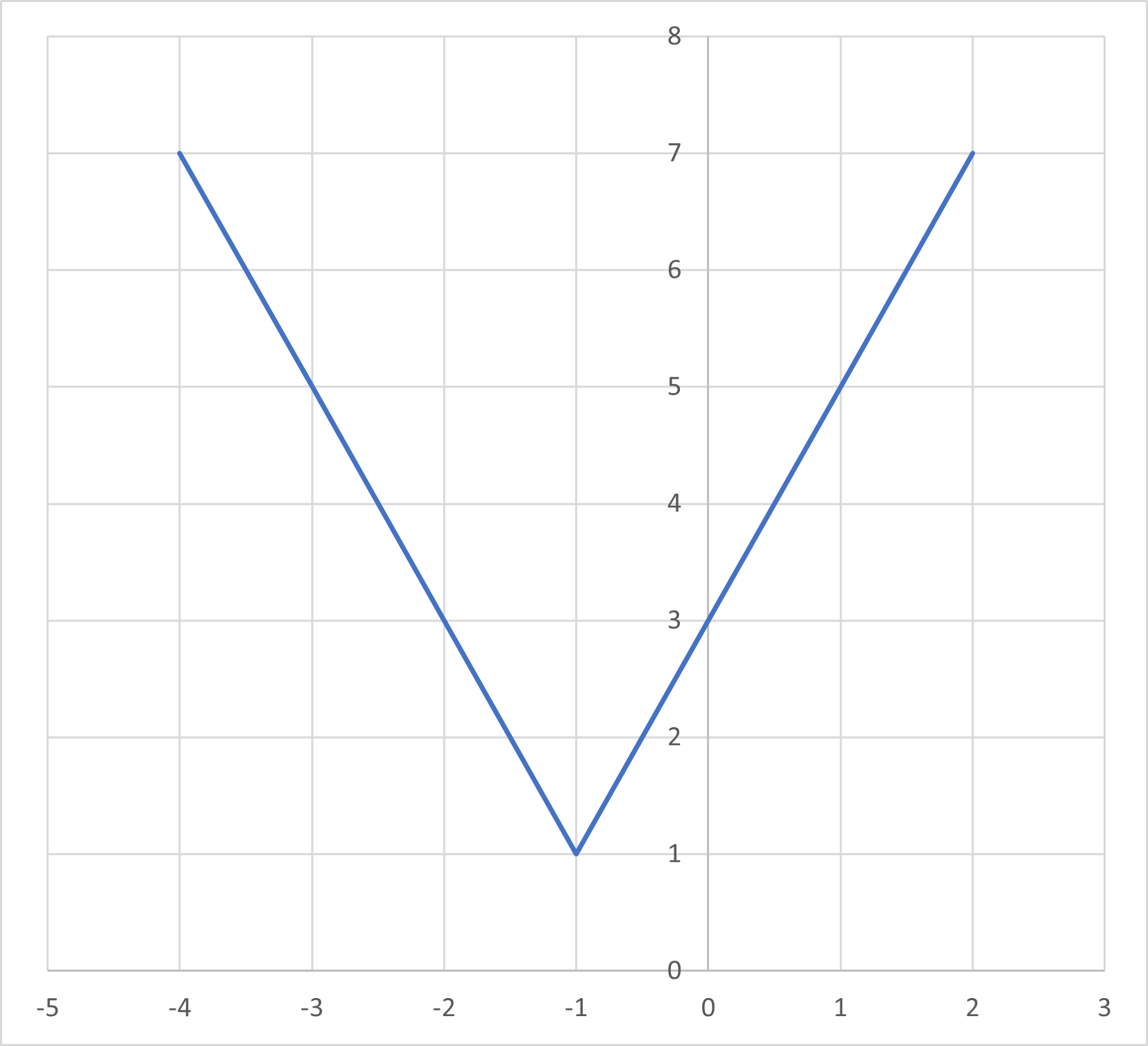
Start with the vertex:

$$\begin{gathered} h=-1 \\ k=1 \end{gathered}$$

Plug these values into the equation:

$$y=a|x+1|+1$$

Find the value for $a$:

Using the point $(0,3)$ as a reference from the graph:

$$\begin{array}{rl}3& =a|0+1|+1\\ 3& =a+1\\ a& =2\end{array}$$

form the final equation using the value for $a$:

$$y=2|x+1|+1$$

Find the graph from an equation

This is the reverse of what we did above. You may be given an equation and be asked to find the graph that would come from it. This question should be a bit easier now, as you can easily find the vertex of the graph $(h,k)$.

A value of $a$ greater than $1$ will cause the graph to become narrower (vertical stretch, like taffy), and a value of $a$ between $0$ and $1$ (a fraction or decimal) will cause it to become wider (vertical shrink, like squishing the parabola or V-shape). If it is negative, the graph will be flipped upside down (reflected over the $x$-axis) compared to normal.

This is all the information needed to determine the graph that most fits the equation you may be given. Locate the vertex and how the value for $a$ affects the graph, whether it is narrower, wider, or upside down.

Other times, they may not give you the graph, but they may ask you what transformations have been made to an equation from the parent function. Parent function means the most basic form of that function. For quadratics, this is $y=x^2$. For absolute values, this is $y=|x|$. For example:

What transformations exist for the function given by $y=2\ast (x+3{)}^2+4$?

Let’s identify $a$, $h$, and $k$:

$$\begin{array}{rl}a& =2\\ h& =-3\\ k& =4\end{array}$$

Given this, we can tell that:

• Since $a$ is $2$, which is positive and larger than $1$, it will be a regular parabola, except it has a vertical stretch by a factor of $2$.
• Since $h$ is $-3$, this graph has undergone a horizontal translation to the left $3$.
• Since $k$ is $4$, this graph has undergone a vertical translation up $4$.