Solving and graphing linear equations

Linear equations always create graphs of straight lines. They can easily be graphed in a variety of ways including creating points using a linear equation, connecting points, and using a slope to extend a line from a single point.

Points from linear equations

If given a linear equation, we can find the points that would make up its graph by picking $x$ values and finding their corresponding $y$ values. With both the $x$ and $y$ values, we create coordinate points that can be drawn on a graph. Let’s try an example of this.

Using the following linear equation, find two points of its corresponding graph.

$$y=x+2$$

We can create any point on this graph by picking a random $x$ value and finding the $y$ value that results from the equation. Let’s pick a few easy ones: $x=0$ and $x=1$.

$$\begin{array}{rl}y& =(0)+2\\ y& =2\end{array}$$

$$\begin{array}{rl}y& =(1)+2\\ y& =3\end{array}$$

Now, we can create the points by joining the $y$ values we found with the original $x$ values: $(0,2)$ and $(1,3)$.

Connecting points

When we have multiple points from a linear function, we can draw the line that would make up its graph. Since we know that linear graphs are always straight lines, all we need is two points in order to graph a linear function. We simply find the location on the coordinate plane of each point and draw a connecting line from one point to the other. Then, extend the line in either direction to show that the line continues on infinitely.

Lines from slope

The slope of a line is the rate at which the line increases or decreases. It is described by the phrase “rise over run” and the equation $m=\frac{(y_2-y_1)}{(x_2-x_1)}$. Using one starting point, we can find more points by applying the slope of the line. For instance, if we start at the point $(1,1)$ and we know that the slope of the line is $\frac{1}{2}$, then we can find our next point using the process below:

The phrase “rise over run” means that we can view the slope as a fraction of $y$ movement over $x$ movement. If the slope is $\frac{1}{2}$, then that means the $y$ value will increase by $1$ and the $x$ value will increase by $2$ at the second point: $(2,3)$.

After we have two points, we are now able to draw a connecting line and find the overall graph of the linear function.

Solving linear equations

The solution to a single linear equation is the point where it crosses the $x$-axis. When a question asks for the solution to a linear equation, you may find it by locating the $x$-intercept or finding the $x$ value when $y=0$.

The solution to two linear equations is the point where the two lines intersect. This can be found by locating the point of intersection on a graph, or by setting the two equations equal to each other and solving for $x$. Let’s review an example to see what this means:

Find the solution to the following linear equations:

$$\begin{array}{rl}y& =3x-2\\ y& =4+x\end{array}$$

If we choose to use a graph, we can graph both of these lines using the methods above and find the point where they intersect:

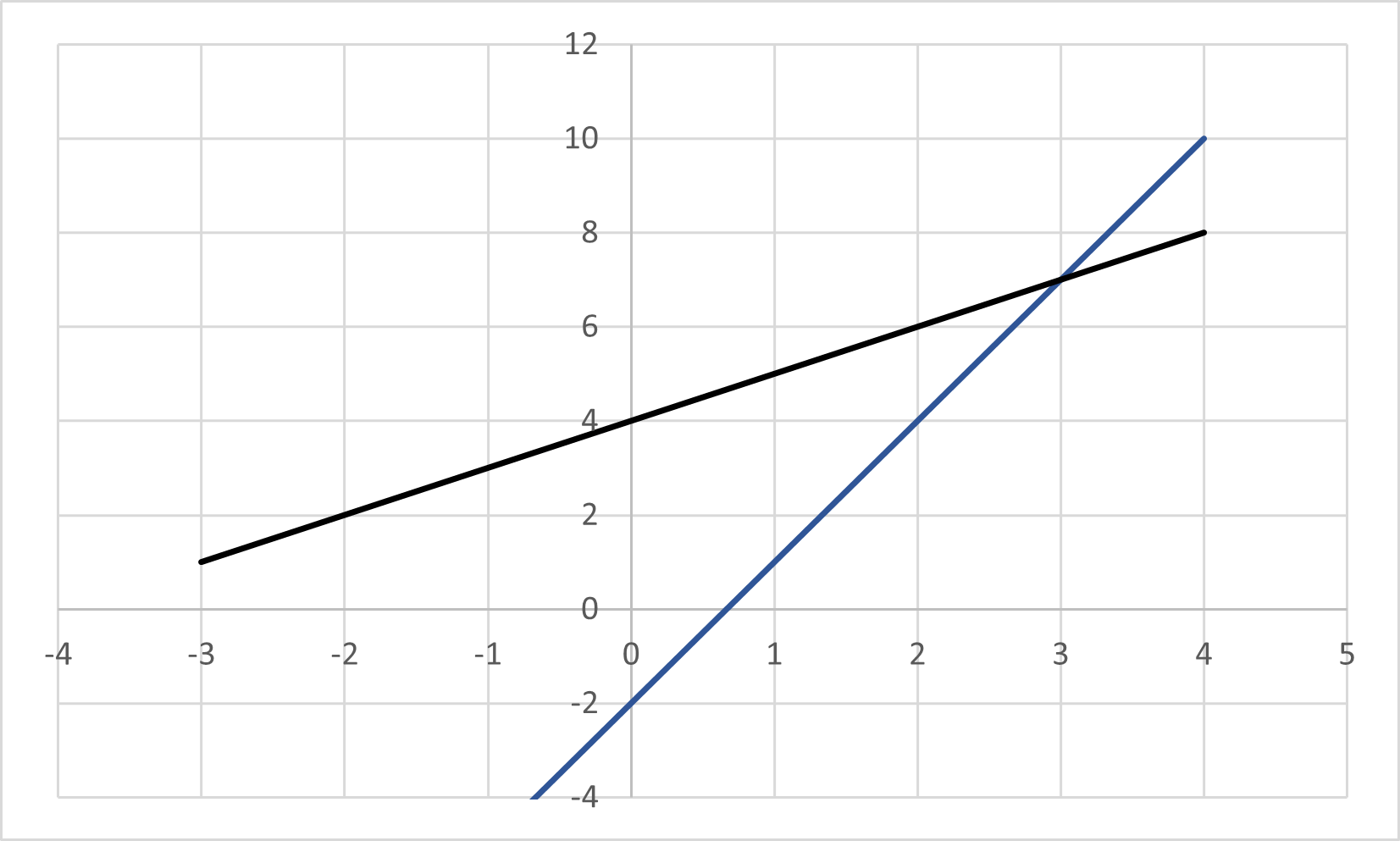
We see that the lines intersect at the point $(3,7)$. This is the solution to the set of linear equations.

Alternatively, we can set the two equations equal to each other to solve for the point of intersection algebraically:

$$\begin{array}{rl}3x-2& =4+x\\ 2x-2& =4\\ 2x& =6\\ x& =3\end{array}$$

Now, plug the value for $x$ into the original equation:

$$\begin{array}{rl}y& =4+3\\ y& =7\end{array}$$

Put the two values together to form a coordinate point, and we get the point of intersection: $(3,7)$