There are three trigonometric functions that we will talk about here: sine, cosine, and tangent. These functions are used to relate the characteristics of a right triangle. That means that these functions will only apply to right triangles—remember that!
The most common way to remember how to use the three trigonometric functions is by the mnemonic device SOH CAH TOA. In this device, S (SOH) stands for sine, C (CAH) stands for cosine, and T (TOA) stands for Tangent. Each of these (SOH CAH TOA) will remind you not only which function is which but also how to use each function properly.
Since we only use these functions with right triangles, we will refer to the one below as we talk about each function and how they are used:
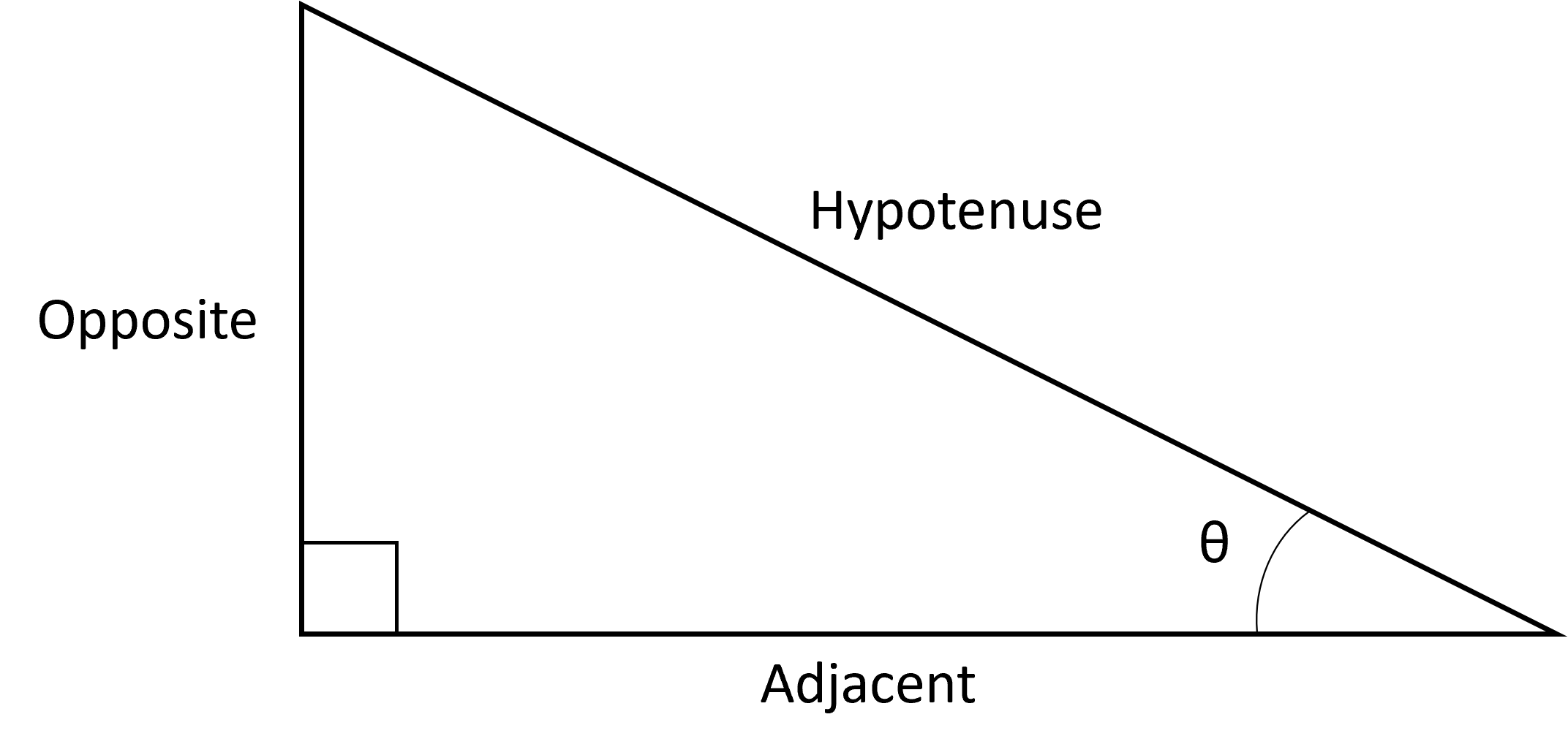
As you can see, the sides of the triangle are labeled as opposite, adjacent, and hypotenuse. These are the remaining letters in the SOH CAH TOA acronym (O, A, and H). In every case, we will use the three letters to write an equation: function first side divided by second side. We use the symbol (theta) to represent the angle instead of .
First, let’s look at SOH. Replacing the letters with their full words, we get Sine Opposite Hypotenuse. Putting the words into the equation above, we get the following equation that tells us how to use the sine function:
We simply plug the values of the triangle side lengths into the equation to find the value of . Suppose the length of the opposite side is 4 and the length of the hypotenuse is 8. The value of would be as follows:
Next, we will look at CAH. This stands for Cosine Adjacent Hypotenuse. Using the exact same rules, we can define the cosine function as the following:
Supposing the length of the adjacent side is and the length of the hypotenuse is , the following equation solves for the value of :
Lastly, we need to take a look at TOA. Following the same rules, TOA stands for Tangent Opposite Adjacent. Let’s form the function for tangent using these terms:
With the opposite length equal to and the adjacent length equal to ,
It is very important that we recognize where theta is in the triangle because the sides (opposite, adjacent, and hypotenuse) are all relative to which angle we are solving for. For instance, if we were to change the angle we are using in the functions to the top right angle of the triangle, the figure would look like this:
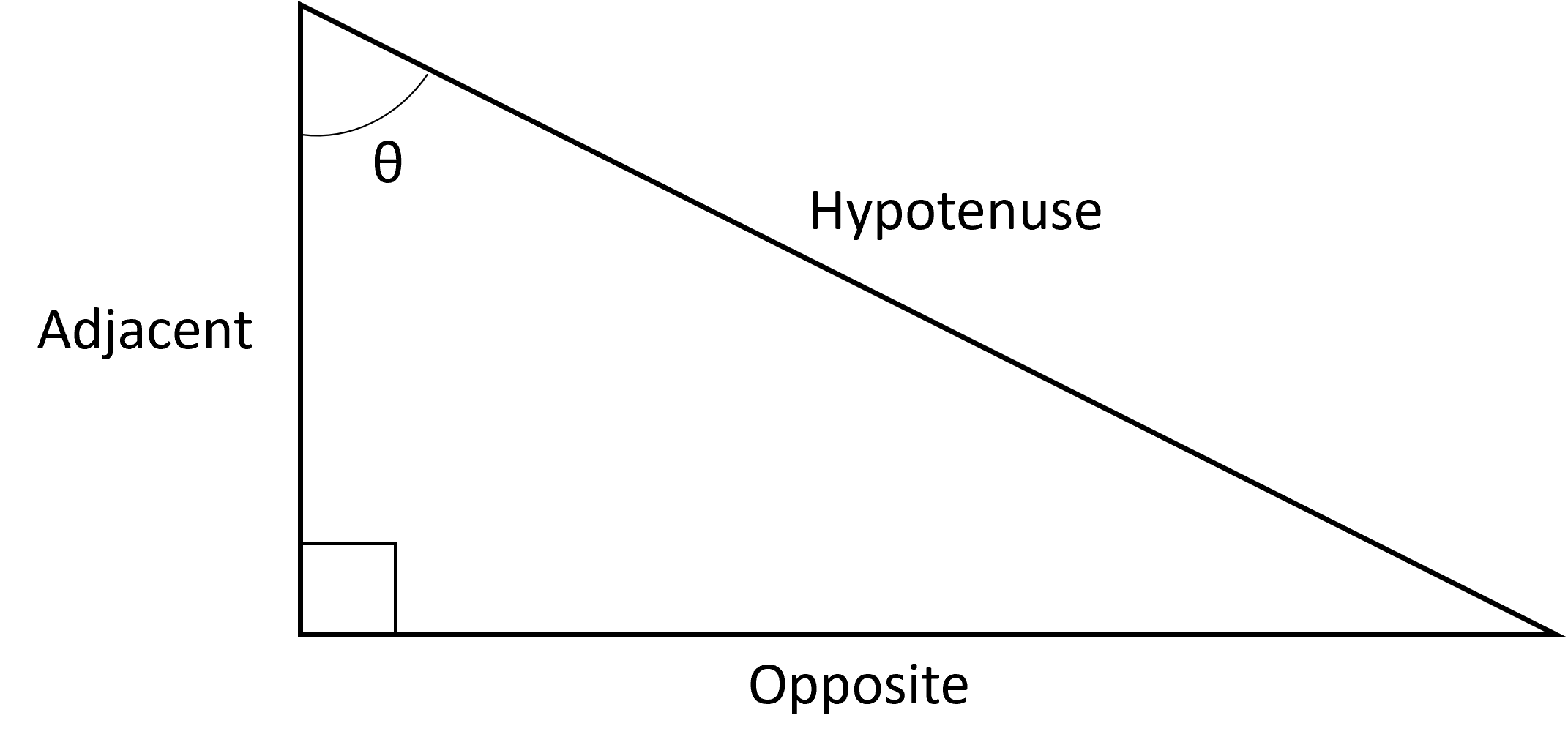
As you can see, the opposite and adjacent sides have swapped spots. This is because they are relative to theta. The “opposite” side is the side of the triangle that is opposite to the angle theta. The “adjacent” side is the side that is next to the angle theta. The hypotenuse, of course, doesn’t change.
This means that you do not need to memorize the locations of the sides in the figures above, but rather think about which side is opposite or adjacent to the angle that you are asked to find.
The most common use of trig functions in algebra is using the functions as described above to find the value of an angle in a trig function. However, sometimes you will be asked to find the measure of a side when given an angle, and other times you may be asked to find the angle theta, itself. This is the difference between finding and finding the value of . To do this, we need to use inverse trig functions.
Solve for the side of a right triangle using trigonometric functions when you are given the measure of one side and one angle. You will have to assess the information you have in order to decide which function you should use. For instance, in the following figure, we have an angle measure and the measure of the opposite side. If a question asks us to find the measure of the adjacent side, then we need a function that uses both the opposite and adjacent sides: the tangent. If a question asks for the measure of the hypotenuse, then we need to use a function that uses both the opposite side and the hypotenuse: sine. Then, we set up the equation for the function we are using and solve for the side we need to find. Try the example below.
Find the measure of side in the figure below.
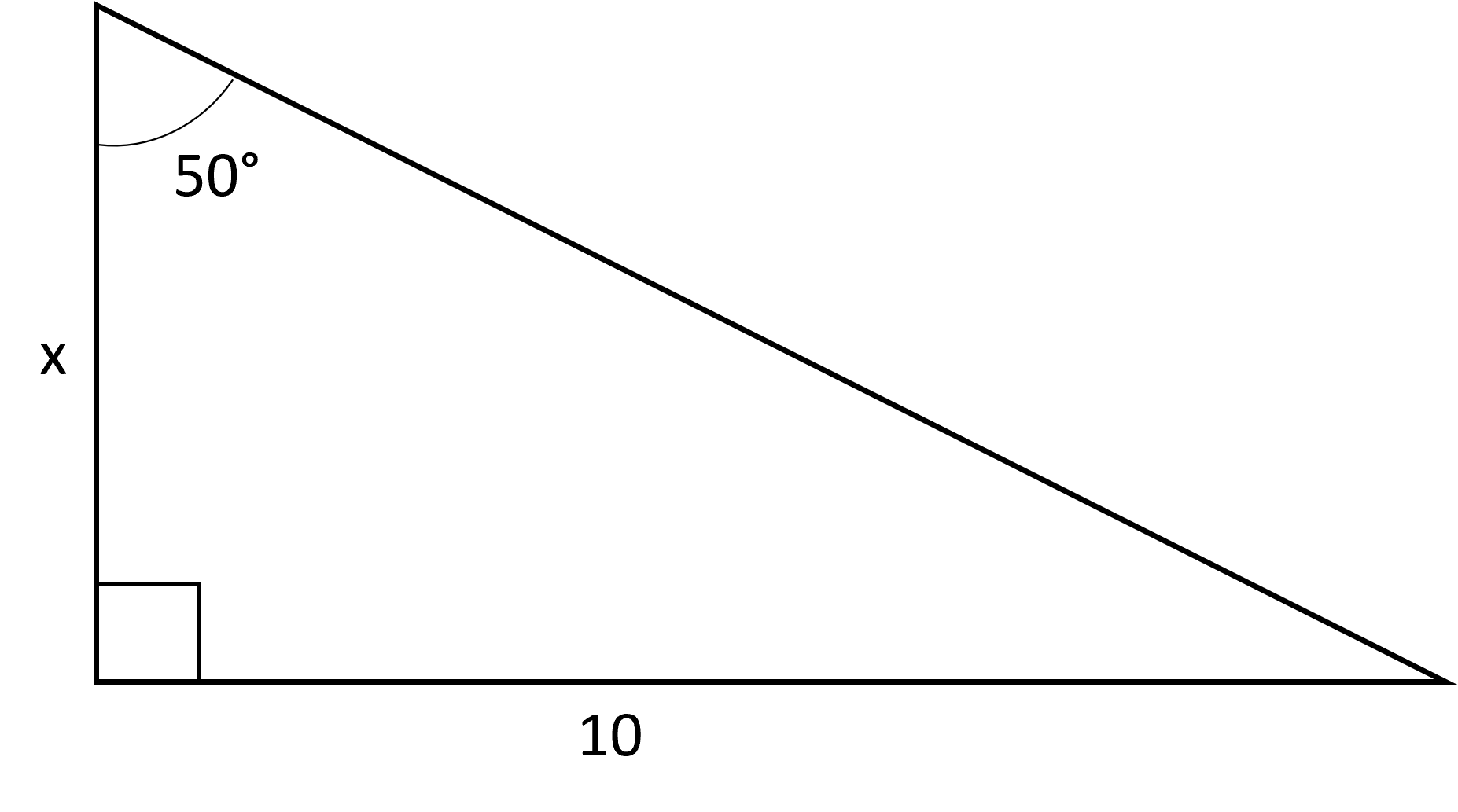
The length of the side is .
When we solve for in algebra we use inverse operations. If is multiplied by a number, we divide by that number to isolate it. This is the same concept as inverse trig functions: it is how we get out of a trig function in order to isolate it. First, make sure your calculator is in degrees!
Inverse trig functions are as follows:
Let’s look at an example.
Find the value of for the following equation:
Isolate theta by taking the inverse cosine of both sides:
The measure of angle is degrees.
Sign up for free to take 3 quiz questions on this topic