Properties of trigonometric functions | Trigonometry | ACT Math

The following graphs display the parent function for a $sin$ , $cos$ , and $tan$ function. Sine and cosine graphs are often referred to as waves, due to their pattern. The characteristics of these wave-like functions will be explored later.

Sine

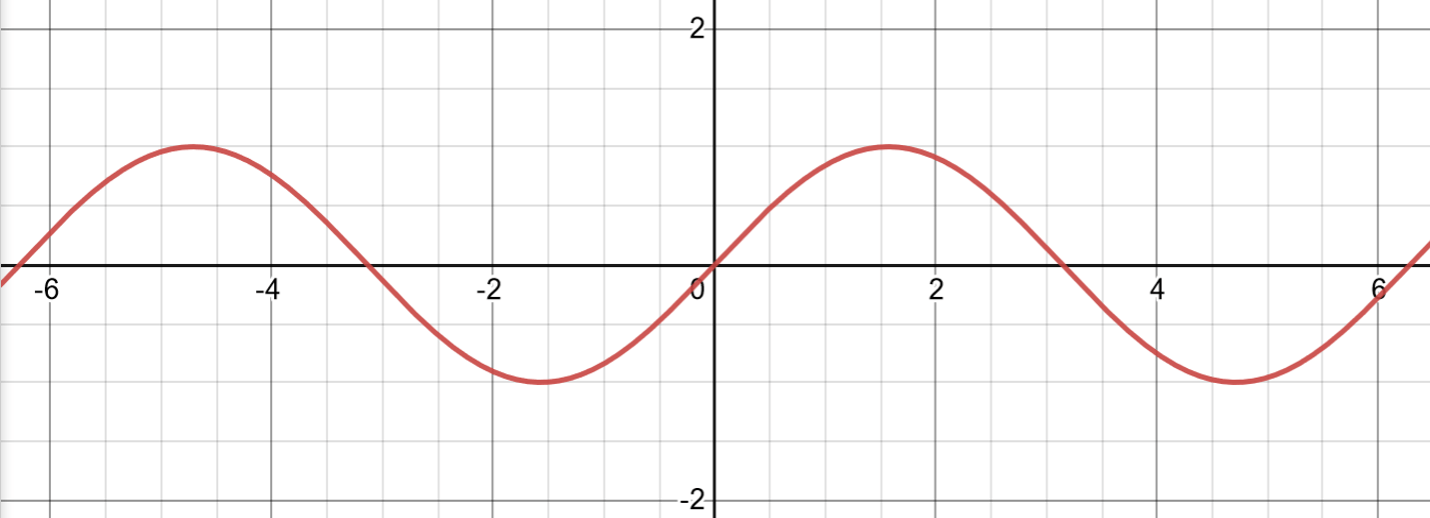
$Properties of trigonometry graph of sin sine function$

As you can see, a sine curve looks like a wave. This means that it has certain wave-like properties such as an amplitude and a period.

The amplitude of a wave is the height of the wave from the $x$ -axis to the peak. Note that the amplitude is the same for the peak above the axis and the peak below the axis. The amplitude of the example above, $y = sin (x)$ , is $1$ .

What the amplitude really tells us is the maximum and minimum value of the graph. This means that the maximum and minimum values of $y = sin (x)$ are $1$ and $- 1$ .

The period of a wave is the distance it takes to complete one wave-like pattern. For a sine graph, you can remember the pattern of the wave by the phrase “middle-high-middle-low-middle.” This suggests that the curve will start at the $x$ -axis, increase to $y = 1$ , decrease to the $x$ -axis again, and finish at $y = - 1$ .

In the example above, the period begins at $x = 0$ and ends at $x = 2 π$ . This means that the period is $2 π$ . The halfway point of the period is at $x = π$ .

Cosine

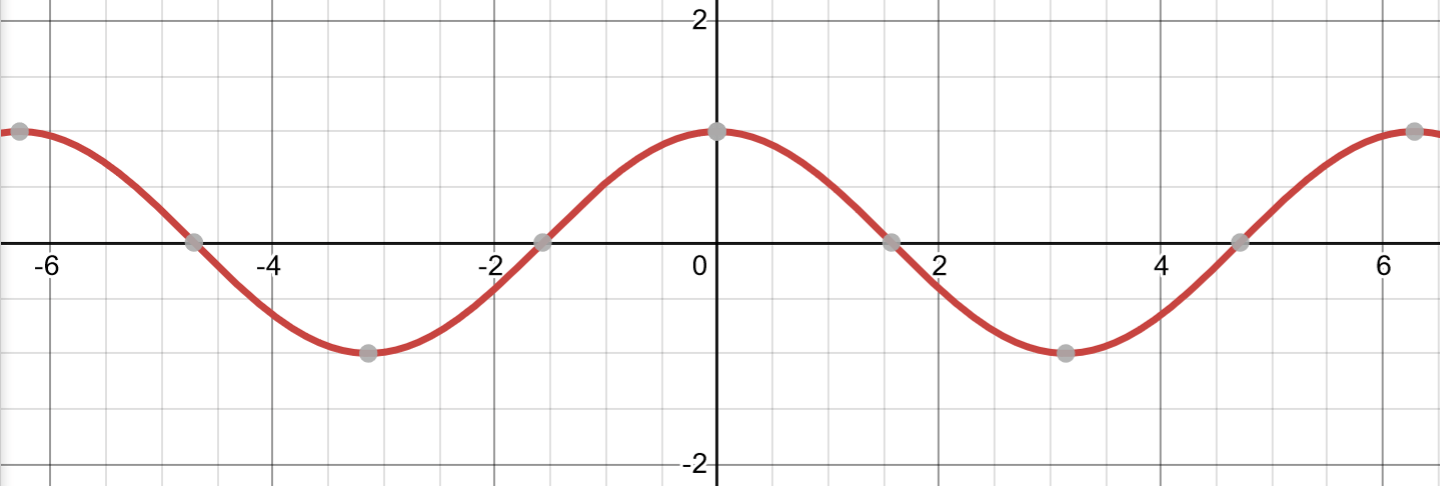
$Properties of trigonometry graph of cos cosine function$

The amplitude of the parent cosine graph is the same as that of the sine graph: $1$ . This means that the maximum value for a $y = cos (x)$ is $1$ and the minimum value is $- 1$ .

The period of the wave is also $2 π$ . However, the wave looks a bit different from the sine wave. The pattern for a cosine wave can be remembered as “high-middle-low-middle-high.” It begins at $y = 1$ at the origin, decreases to $y = - 1$ , then increases back to $y = 1$ .

Tangent

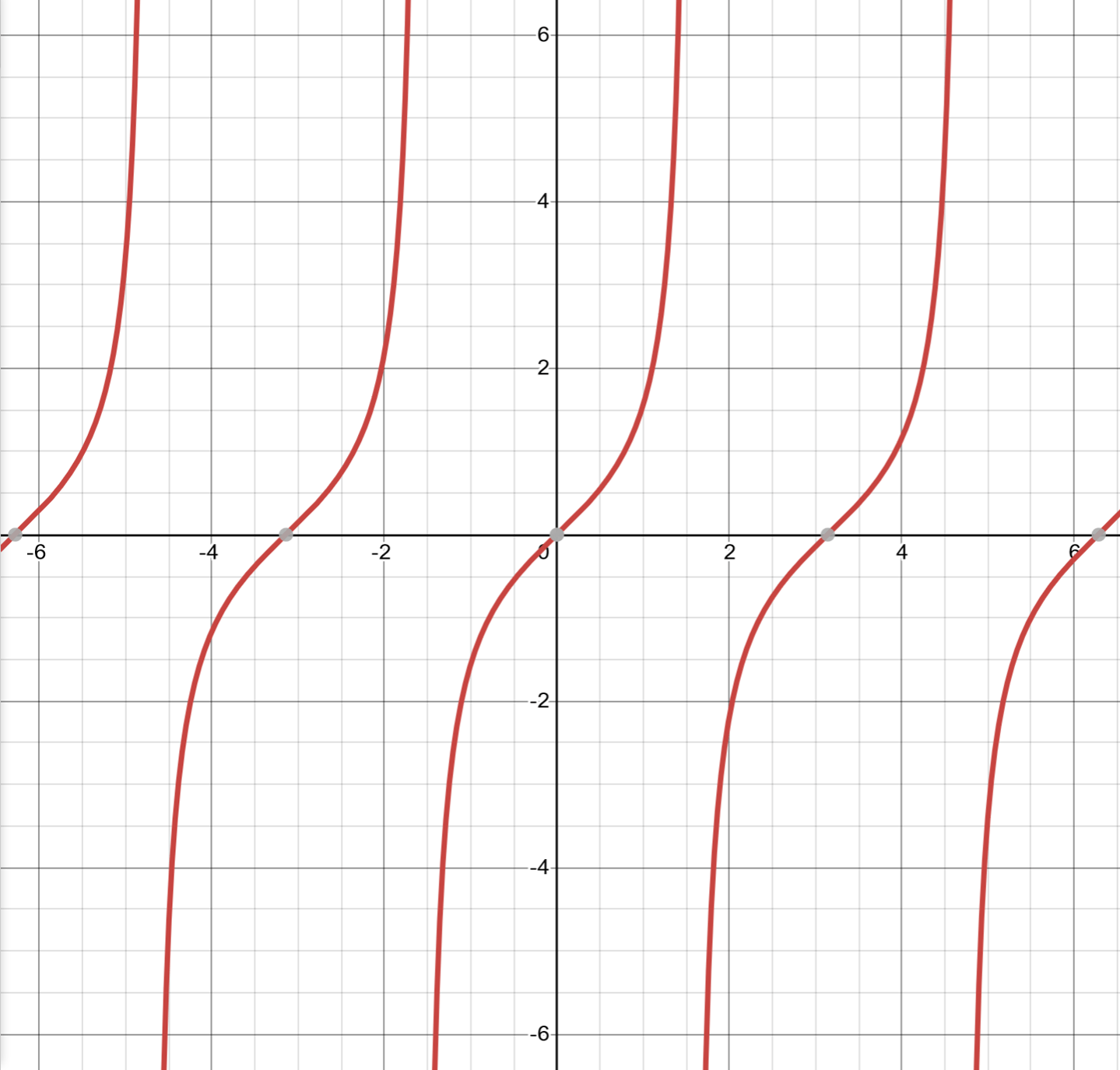
$Properties of trigonometry graph of tan tangent function$

The graph of $y = tan (x)$ is much different from sine and cosine. As you can see, it is not represented by a wave like the others. Instead, you will see a cubic-like curve that repeats several times. Note that there are vertical asymptotes that separate each curve. If you need a refresher on asymptotes, review the chapter Nonlinear functions and graphs.

Beginning at the origin, you will see that the curves intersect the $x$ -axis at intervals of $π$ in both the positive and negative $x$ directions. The vertical asymptotes occur at intervals of $π$ in both $x$ directions as well, but beginning at $x = π /2$ .

Nonparent functions

You will often see sine and cosine functions that are a bit different from their parent functions. In these cases, we need to know how to find the amplitude and period without using a graph.

You can find the amplitude of a sine or cosine wave by finding the value in front of the function. The function $y = sin (x)$ has no number in front of the function, so we must assume that there is a $1$ . That is why the amplitude of the functions above is $1$ . Here is another example:

Find the amplitude of the following function:

$y = 3 * sin (2 x)$

The amplitude of the function is $3$ . This is also the maximum value of the function. The minimum of the function is $- 3$ .

Find the period by figuring out what value you need to multiply into the inside of the function to get the coefficient of $x$ to equal $2 π$ . Normally, the inside of the function is just $x$ . The coefficient here is $1$ , and we have to multiply $1$ by $2 π$ to get it to equal $2 π$ . Here is another example of finding the period:

Find the period of the following function:

$y = 3 * sin (2 x)$

Find out what value we need to multiply into the function to get a coefficient of $2 π$ for $x$ . The current coefficient is $2$ .

$2 * period = 2 π$

The period of the function is $π$ .

Trigonometric identity

There are several trigonometric identities, which are the relationships between different trigonometric functions. However, for the ACT test you will only need to know one of them:

$sin^{2} (x) + cos^{2} (x) = 1$

The $x$ in this identity can be anything, as long as the value is identical between the two functions. For instance, the functions could have $2 x^{2}$ inside them instead of just $x$ :

$sin^{2} (2 x^{2}) + cos^{2} (2 x^{2}) = 1$

Key points

Sine wave. The sine function takes the form of a wave that follows the pattern “middle-high-middle-low-middle”.

Cosine wave. The cosine function takes the form of a wave that follows the pattern “high-middle-low-middle-high”.

Tangent curves. The tangent function takes the form of an infinite number of curves that look like cubic functions. The curves are spaced at a distance of $π$ apart. Intersections of the x-axis span in the positive and negative x directions starting at $x = 0$ , and the vertical asymptotes span in both directions starting at $x = π /2$ .

Amplitude. The amplitude of a sine or cosine function is the height of a wave from the axis to the peak. Find this by locating the number multiplied in front of the function.

Period. The period of a sine or cosine function is the length of a single cycle of the wave. Find the period by figuring out what value must be multiplied inside the function to get the coefficient of $x$ to be $2 π$ .

Trigonometric identity. $sin^{2} (x) + cos^{2} (x) = 1$ where $x$ can be any value as long as it is identical in both functions.