Domain and range

A domain is the set of all possible $x$-values (inputs) of a function. You can determine the domain from a table, an algebraic function, or a graph. There are also multiple ways to write a domain, depending on what the inputs look like.

Tables

Refer to the following table:

In the table above, the $x$-values are $1$, $2$, $3$, $4$, and $5$. Those values make up the domain.

To write this domain properly, you have two options:

• $\{1,2,3,4,5\}$
• $[1,5]$

The first method lists each input explicitly inside curly braces.

The second method uses an interval: it shows the first and last values inside square brackets. You only use this square-bracket method when the domain includes every whole number between the two endpoints.

Algebraic functions

Refer to the following function:

$$y=\frac{1}{x}$$

Here, you aren’t given a list of inputs, so you have to decide which $x$-values are allowed. A useful question is: are there any values that $x$ cannot equal?

In this function, $x$ is in the denominator. A denominator can’t be $0$, so $x\ne 0$. Other than that, $x$ can be any real number.

Because there are infinitely many possible $x$-values, you can’t list them one by one. Instead, write the domain using interval notation:

$$(-\infty ,0)\cup (0,\infty )$$

Notice two key features:

• Parentheses mean the endpoint is not included (like an open circle on a graph).
• The symbol $\cup$ means “union,” which combines the two intervals into one set.

Graphs

Refer to the following graph:

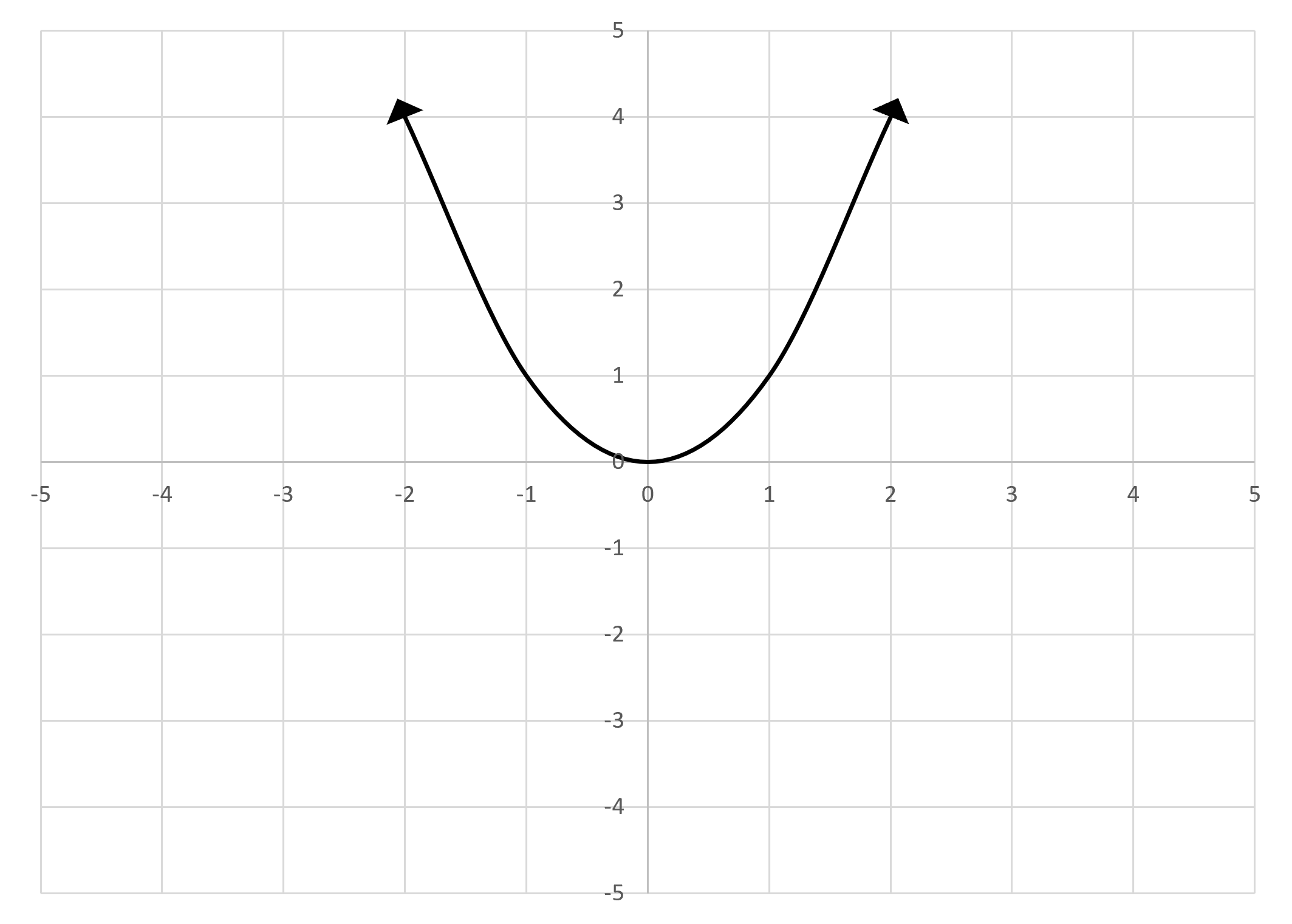
The arrows show that the curve continues forever in both directions. That means the $x$-values extend infinitely to the left and infinitely to the right.

So, the domain is $(-\infty ,\infty )$.

Range

The range is the set of all possible $y$-values (outputs) of a function. Like the domain, you can find the range from a table, an algebraic equation, or a graph. You write the range using the same notation styles as the domain - you just focus on the $y$-values instead of the $x$-values.

We will use the same examples as above to find the range for each form of a function.

Table

Refer to the following table:

The $y$-values are $2$, $4$, $6$, $8$, and $10$, so the range is $\{2,4,6,8,10\}$.

You can’t use the square-bracket method here because the outputs do not include every value between $2$ and $10$.

Algebraic function

Refer to the following function:

$$y=\frac{1}{x}$$

You already know $x$ can be any real number except $0$. Now ask the same kind of question for outputs: are there any values that $y$ cannot equal?

For $y=\frac{1}{x}$, the output can get very large (positive or negative) as $x$ gets close to $0$, and it can get very close to $0$ as $x$ becomes very large in magnitude. But $\frac{1}{x}$ can never equal $0$.

So, the range is $(-\infty ,0)\cup (0,\infty )$.

Graph

Refer to the following graph:

The curve extends infinitely upward (in the positive $y$-direction) and has a lowest point at $y=0$. It does not go below the $x$-axis.

So, the range is $[0,\infty )$. You use a square bracket at $0$ because the function actually reaches $y=0$. You use a parenthesis at $\infty$ because the function increases without bound but never equals infinity.