Lines and coordinates | Coordinate geometry | ACT Math

A coordinate plane is the graphing space used to show functions. It is separated into four quadrants, as indicated below:

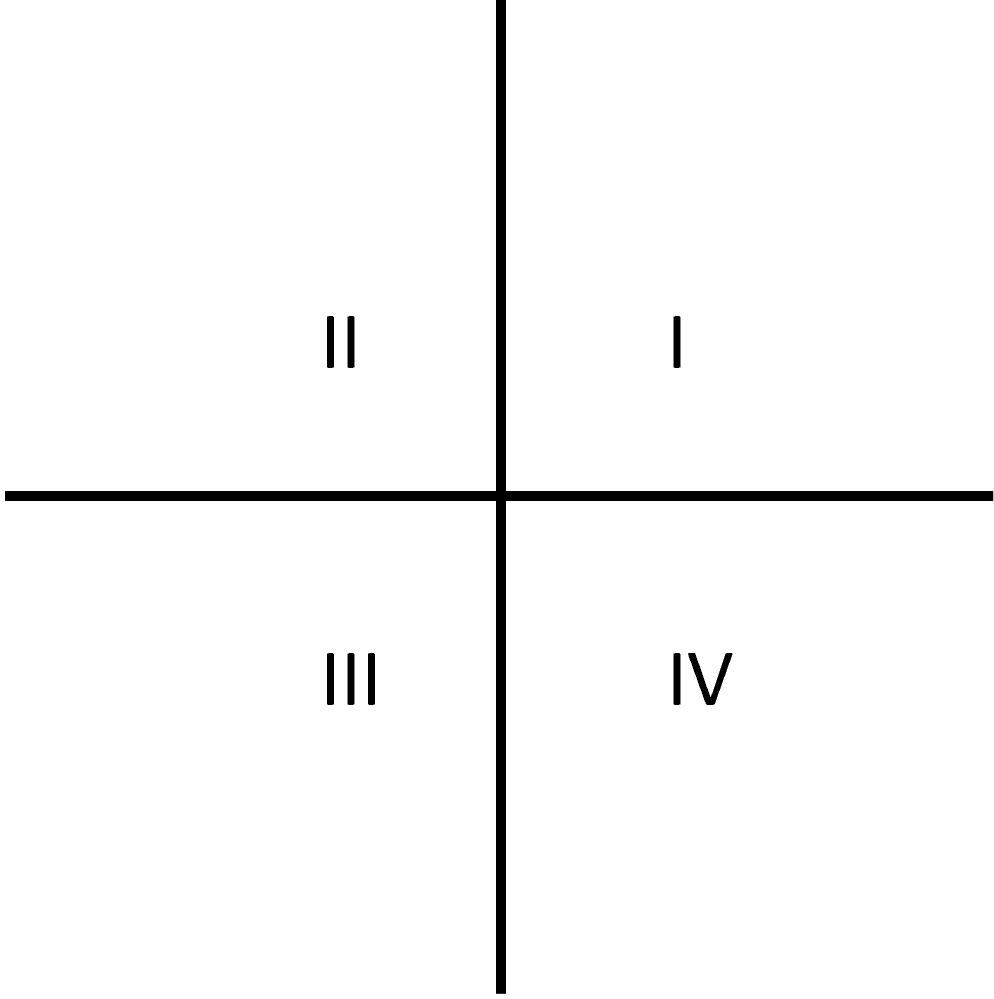
$Graph of cartesian coordinate plane quadrants$

We use coordinate planes to measure properties created by functions. In order to measure these properties, we use the $x$ (horizontal) and $y$ (vertical) axes to measure coordinate points. These points appear as ( $x$ -value, $y$ -value).

Primarily, we measure the properties of lines. Some important properties include two-line interactions like perpendicular and parallel lines.

Definitions

Perpendicular: Perpendicular lines are lines that create a right angle when they intersect.
Parallel: Parallel lines are lines that run next to each other and never intersect.

Another important property is the slope of a line. We will explore this next. We will discuss the midpoint and distance formulas with lines later in this chapter.

Slope of a line

The slope of a line indicates the rate at which the line changes. A slope is an incredibly useful property of any line, that is why we spend so much time figuring out how to find it. Find the slope by measuring how far a line travels in the $x$ and $y$ directions between two points, and dividing the $y$ value by the $x$ value. This is what we refer to as “rise over run.”

For in-depth instruction on finding the slope of a line, review the chapter Standard form of linear equations.

Parallel lines have the exact same slope. This is why they never intersect. They are at the exact same angle forever, so they never touch. Perpendicular lines have slopes that are opposite reciprocals of each other. This means that the slopes have the opposite sign (positive/negative) and you can get one slope by dividing $1$ by the other slope. Let’s take a look at a few examples.

What is the slope of a line parallel to the line given by the equation $y = 3 x + 7$ ?

The slope in this equation is $3$ . If the lines are parallel, they will have the same slope. So, the answer is $3$ .

What is the slope of the line perpendicular to the line given by the equation $y = 3 x + 7$ ?

Same line, different question. To get the opposite reciprocal of the slope ( $3$ ), we change the sign and divide $1$ by the slope.

$perpendicular slope perpendicular slope = - 1/ slope = - 1/3$

So the answer to this question is $- \frac{1}{3}$ .

Midpoint

The midpoint of a line is self-explanatory: it is the point at the very middle of a line. The midpoint can sometimes be tricky because we have to find the middle of both the $x$ and $y$ aspects of the line. For instance, in the example below finding the midpoint is more difficult than simply pointing at the middle. Instead, we have to find the middle values of both the $x$ and $y$ movements as a coordinate point:

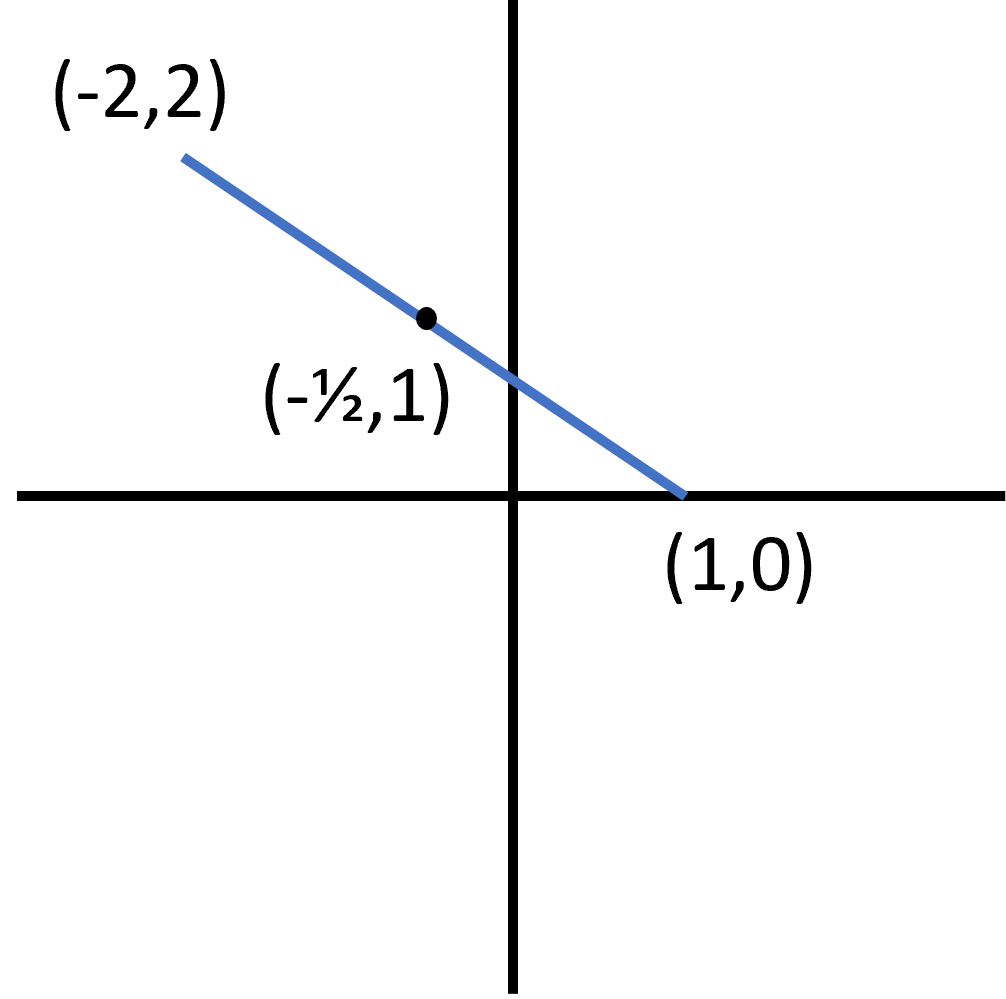
$Line graph of midpoint on xy coordinate plane$

We can find the $x$ value of the midpoint by finding the middle between $- 2$ and $1$ . How do we do that? We take the average of the two points:

$x_{mi d} = \frac{( - 2 + 1 )}{2} = - \frac{1}{2}$

The same can be done for the $y$ value:

$y_{mi d} = \frac{( 2 + 0 )}{2} = 1$

So, if we combine this information together, we get the midpoint formula:

$(x_{mi d}, y_{mi d}) = (\frac{( x _{1} + x _{2} )}{2}, \frac{( y _{1} + y _{2} )}{2})$

As you can see, the formula does exactly what we did above! Try an example on your own below:

What is the midpoint of the line below?

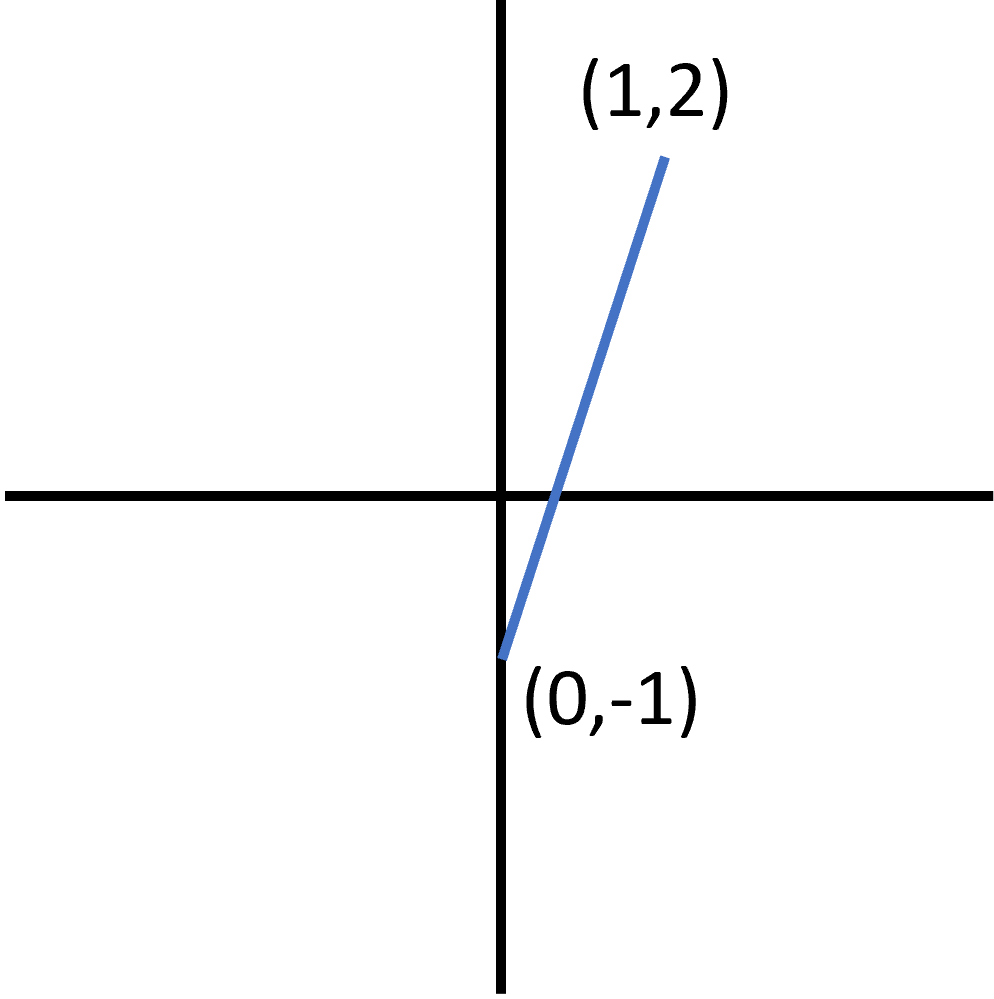
$Line graph of midpoint on xy coordinate plane$

(spoiler)

$(x_{mi d}, y_{mi d}) (x_{mi d}, y_{mi d}) (x_{mi d}, y_{mi d}) = (\frac{( x _{1} + x _{2} )}{2}, \frac{( y _{1} + y _{2} )}{2}) = (\frac{( 0 + 1 )}{2}, \frac{( - 1 + 2 )}{2}) = (\frac{1}{2}, \frac{1}{2})$

The midpoint of this line is $(\frac{1}{2}, \frac{1}{2})$ .

Distance

The distance between two points essentially measures the straight line from one point to another. It is a lot like finding the hypotenuse of a right triangle, and even shares a very similar formula to the Pythagorean theorem:

$D i s t an ce = (x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}$

Let’s do an example together:

If a person runs $1$ mile west, then $2$ miles north, and lastly $1$ mile west, what is the distance from his starting point to his final destination?

We first need to determine the starting and ending points so that we can use the formula. If we consider the starting point to be $(0, 0)$ , then we can find our $x$ and $y$ values by following our directions:

For $x$ , we travel $1$ mile to the left, then $1$ more mile to the left. So, the final $x$ value will be $- 2$ .

For $y$ , we travel $2$ miles up. So, the final $y$ value will be $2$ .

Putting this together, our ending point is $(- 2, 2)$ . All that’s left is to put these two points into the distance formula:

$d d d d d = (x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2} = (- 2 - 0)^{2} + (2 - 0)^{2} = 4 + 4 = 8 \approx 2.8$

The distance from the starting point to the ending point is $8$ or about $2.8$ miles.

Key points

Coordinate plane. This is the graphing area for functions. The quadrants are numbered beginning in the top right quadrant and going counterclockwise around the origin.

Perpendicular. These lines form a right angle when they intersect.

Parallel. These lines run together and never intersect.

Slope. This is the rate of change from one point to another. It is found by dividing the movement in the $y$ direction by that of the $x$ direction.

Midpoint. The middle point of a line is the midpoint and is found by identifying the middle between the $x$ and $y$ values of the endpoints of the line. $(x_{m}, y_{m}) = (\frac{( x _{1} + x _{2} )}{2} + \frac{( y _{1} + y _{2} )}{2})$

Distance. This is the distance between any two points. $D i s t an ce = (x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}$