A linear equation is an equation that produces a straight line on a graph, as opposed to other equations that produce curves. The three types of linear equations that will be addressed in this chapter are standard form, point-slope form, and slope-intercept form. You can recognize an equation as linear if its highest exponent on a variable is .
The standard form of a linear equation is:
where and are variables, and , , and are any integers. This form is useful because we can solve for the -intercept and -intercept easily. To find the -intercept, we set and solve for . If we want to find the -intercept, we set and solve for . One way to remember this is that you should solve for the same variable for which you want the intercept. If you want the -intercept, then you will need to solve for .
We can also use this form to find the slope with the formula where m is the slope of the line. If we do not want to solve the equation algebraically to find the -intercept, we can simply use the formula to quickly find this value.
We will explore a few examples to ensure that we can recognize the key points of a linear equation and find the and intercepts.
Is the following equation a linear equation? If so, find the and intercepts.
Is the highest exponent on the variables ? Yes.
This is a linear equation. There is a minus sign in place of the usual addition sign, but it is still linear.
-intercept: set
Solve for :
The -intercept is .
-intercept: set
Solve for :
The -intercept is
Try a few more examples before moving on to the next section. You will notice that even if an equation is not in standard form, it can still be linear because we can turn it into standard form.
Is the following equation a linear equation? If so, find the and intercepts.
Is the highest exponent on the variables ? Yes.
This is a linear equation. The form looks very different, but we can rearrange it using algebra so that it appears .
-intercept: set
Solve for :
The -intercept is .
-intercept: set
Solve for :
The -intercept is .
Is the following equation a linear equation? If so, find the and intercepts.
Is the highest exponent on the variables ? No, the highest power is .
This is not a linear equation. We will not solve for the intercepts.
The second form of linear equations is point-slope form. This form is useful when you want to find the slope between two points. You may have a graphed line with two points on it, two coordinate points given in a problem, or even just an equation that you could use to find two points. A linear equation in point-slope form looks like
Where is the slope, the variables with the subscript of are the coordinates of the first point, and the variables with the subscript of are the coordinates of the second point. This comes from the formula for slope, which you may be more familiar with,
You can more easily remember this formula by the phrase “rise over run.” This means that to find the slope of a line, you count how far the line “rises” in the -direction, and then divide that by how far the line “runs” in the -direction. is the “rise” and is the “run.” Try a few examples.
What is the slope of the line formed by the points and ?
How far does the line “rise” from the first point to the second point? .
How far does the line “run” from the first point to the second point? .
Slope is rise over run,
You may notice that doing the rise over run method actually caused us to perform the full point-slope formula. At the end of the day, either way you remember this equation will work perfectly well.
Find the slope of the following line:
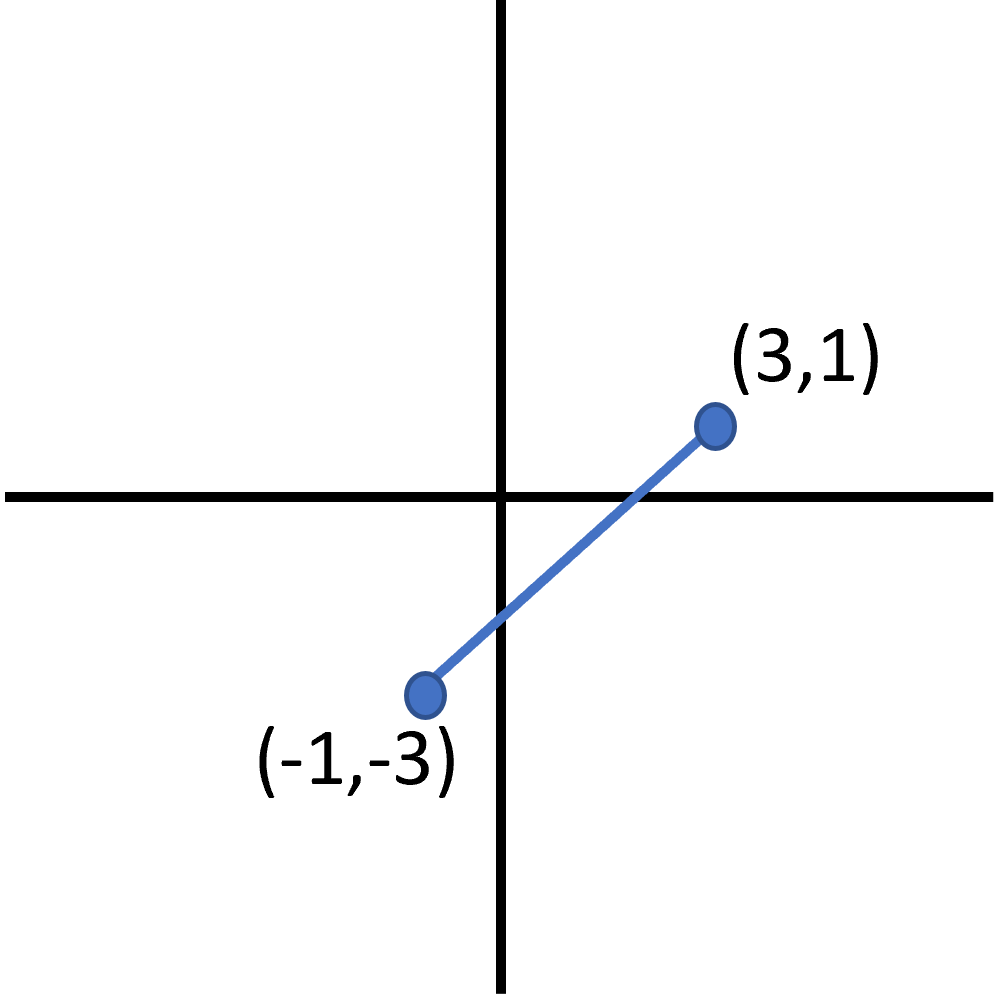
Rise over run
The slope of this line is .
The third form of linear equations we will talk about is slope-intercept form. It is very useful because it helps us determine the slope and the -intercept just by looking at the equation. However, the equation must look a specific way in order for it to work. We call this the slope-intercept form, and it looks like , where and are variables, represents the slope, and represents the -intercept. It is slightly confusing that we choose to use variables and instead of and , but this helps us remember that the equation must be in slope-intercept form in order to determine the slope and the -intercept.
If you see an equation in this form, then you can find the slope to be whatever numbers are attached to . It’s as easy as it sounds. Check out this example.
What is the slope of this equation?
In this case, . Or in other words, . The slope is therefore .
We can also use point-slope form as a way to get the equation of a line into slope-intercept form. For example, if we are told that the slope of a line is and the line goes through the point , we can use point-slope form to get to slope-intercept form, which will directly tell us the -intercept. To do this, instead of using and , we just leave them as and in point-slope form.
Now, we rearrange the equation to look like slope-intercept form.
Now we have the equation of that line, and we can clearly see that the -intercept is .
Sign up for free to take 7 quiz questions on this topic