Arithmetic and geometric sequences

Sequences

A sequence is a list of numbers that follows a pattern from one term to the next. A sequence generally goes on forever, always following the same pattern. The most common patterns for sequences are arithmetic and geometric sequences. Arithmetic sequences involve patterns of adding, and geometric sequences involve patterns of multiplying. We always have multiple ways to understand sequences, but the main two that we will discuss involve expanding the sequence of numbers by hand or using a formula that pertains to the type of sequence.

We will be using some particular vocabulary in this section very frequently. A term is defined as a number in the sequence. The first number is considered the first term. The letter $n$ will represent the numbered term in a sequence. The first term, second term, third term, and so on will be referred to as the $n$th term to signify that it could be any term in the sequence.

Arithmetic sequences

The term arithmetic sequence is really just a fancy way to describe a pattern of numbers. This form of sequence is characterized by a pattern of addition. This means that each term in an arithmetic sequence is separated by the same amount. The second term in the sequence is the same amount larger than the first term as the third term is from the second term. Let’s make this clear on a number line:

As you can see, this is a very simple pattern. The same pattern will continue forever in this number line. So, we can simply count up this pattern until we get to the term that we are looking for. Alternatively, we can use this formula to immediately determine the term that we want to find:

$$x_n=(\text{first term})+\text{difference}\ast (n-1)$$

The ACT test will not require you to use a specific method, so you will just need to decide which method you are more comfortable with. For instance, instead of being asked to find the pattern by which the sequence increases, you may be tasked with finding the value at a given point, like below:

Find the $9$th term in the arithmetic sequence that begins as follows: $1,5,9,...$

In this case, you may approach the solution to these types of problems using one of our two reliable methods:

1. Write out the numbers as a list until you reach the term you are looking for. (The pattern is adding four, so it continues $1,5,9,13,17,21,25,29,33$. The $9$th term in the sequence is $33$)

2. Follow the formula to immediately determine the term that you want to find without writing out any of the sequence: $x=1+4\ast (9-1)$, $x=33$

Whether you decide that it is easier to solve this problem intuitively or formulaically, be sure to remember that arithmetic sequences are number lists with additive patterns!

Geometric sequences

Geometric sequences are much like arithmetic sequences: they are lists of numbers that increase by a pattern. The primary difference is that geometric sequences increase by multiplying by a number. For instance, instead of adding two to each term, a geometric sequence may be multiplying each term by two. Compare this idea to the number line below:

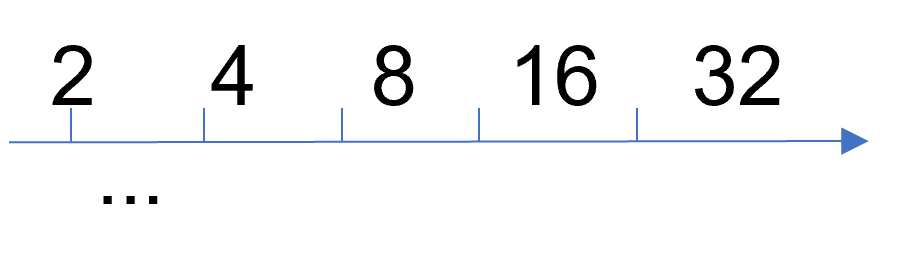
Just as with arithmetic sequences, this pattern will go on forever. Listing out the sequence of numbers is the safest way to locate a certain term within the sequence, but the following formula may also be used to determine the value of a given term:

$$x_n=(\text{first term})\ast (\text{multiplying number}{)}^{(n-1)}$$

In a similar way as above, we may write out a list of numbers, multiplying by the same factor each time we move forward a term. If the factor, or multiplying ratio, is $4$ and our starting term is $1$, then our sequence is as follows: $1,4,16,64,256,1024,4096,16384,\dots$ This sequence increases at a much higher rate than an arithmetic sequence would, but the process is the same.

Summing sequences

When you are not asked to find the value of a certain term in a sequence, it is very common that you will be tasked with finding the sum of the sequence up to a given term. The simplest way to do this is by intuition: writing out the terms of a sequence and adding all the terms up to the point you are given. However, some more difficult questions may not give you all the information necessary to do this, or they may give you the sum and ask for the difference or ratio.

In these more advanced cases, you will need to refer to the following formulas, which sum up the series to a given term:

Let’s review an example of how we can do this in the simplest way:

What is the sum of a geometric sequence with five terms where the first term is $4$ and the multiplying ratio is $3$?

First, we should write out the sequence as best we can. We are given the starting number and we are given the factor by which we will multiply each term. So, we will go ahead and begin listing numbers until we reach our goal term ($5$th term):

$4,12,36,108,324,\dots$

Now that we have the first five terms, we can find “the sum of the sequence at the fifth term.” What would that be?

Again, the simplest way to perform these operations is by listing out the terms and adding them up until you get to the term you are asked to find. However, in cases where you do not have sufficient information to do this, you may need these equations to calculate the sum at a given term.