Circles

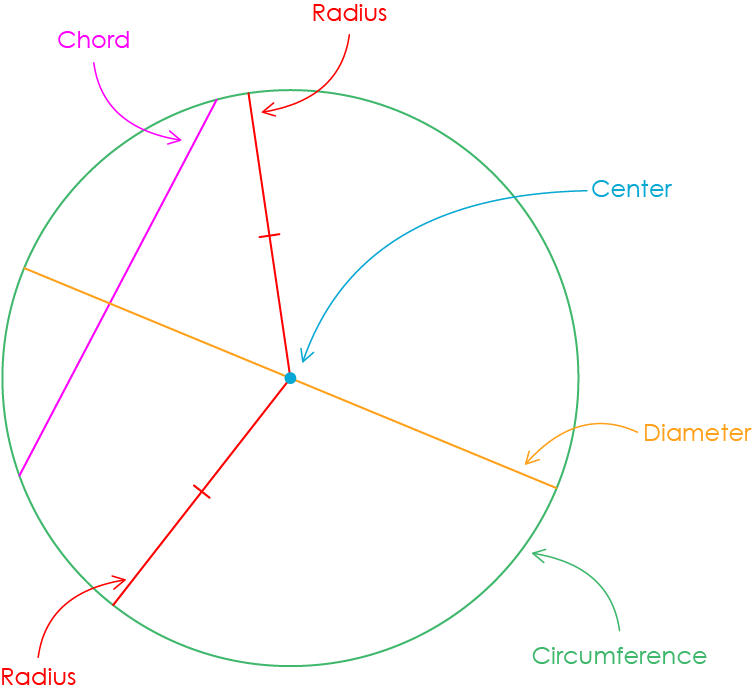
Circles have a lot of terms used to describe different parts - take a look at the diagram below.

Any time you see a problem with a circle, you’ll likely need at least one of these two equations.

Let’s try using these equations to solve an example problem.

What must be the radius of a circle if both the area and the circumference of the circle are equal in terms of units?

First, let’s make sure we understand the question. The phrase in terms of units is a bit distracting. Sometimes the test writers like to be very explicit, as technically, the circumference would be measured by its 1-dimensional length of $X$ meters, whereas the area would be measured by its 2-dimensional area of $X$ square meters. The question is confirming that it’s okay for us to leave out the units and use just the $X$ number for comparison instead.

We certainly know that not all circles have a circumference equal to their area. However, the question asks us to find the specific circle where the circumference is equal to the area. We can simply set the area and circumference equations equal to each other, and solve for the radius of this circle.

$$\begin{array}{rl}\text{area}& =\text{circumference}\\ \pi r^2& =2r\pi \\ r^2& =2r\\ r& =2\end{array}$$

The only circle with an area equal to its circumference has a radius of $2$.

The central angle theorem (CAT)

The central angle theorem (CAT) is a key rule that can make some seemingly impossible problems quite easy. The theorem states that if you put any two points on the edge of a circle, the angle formed between those points and the center of the circle will be twice the size of the angle formed by the two points and any third point on the circle. We know that’s a mouthful - it’s easier to visualize:

In the diagram above, points B and F are the centers of their respective circles. According to the central angle theorem, we can make the following equations:

• $2\ast \angle \text{CAD}=\angle \text{CBD}$
• $2\ast \angle \text{GEH}=\angle \text{GFH}$

Note that the third point can be anywhere on the edge of the circle, and the ratio still holds true.

This still works even if the central angle is 180 degrees - the outside angle will then be 90 degrees. This is an important point because it illustrates that any right triangle that is inscribed inside a circle must have a hypotenuse that is the diameter of the circle. In the figures below, B and F are the centers of their circles.

Let’s see how this comes into play with an example question.

Points A and B are the centers of their respective circles, and both circles have the same radius.

Quantity A: $y$
Quantity B: $x$

Try to solve this using the central angle theorem.

Let’s start by solving for $y$. Using the central angle theorem, we know that $y$ will be double the size of the $44^{\circ }$ angle, making $y=88$.

Now let’s focus on $x$, which is a bit trickier to solve. The arrow shape inside the circle is actually a quadrilateral. The sum of interior angles for any $n$-sided shape is equal to $(n-2)\ast 180$, which for a quadrilateral is equal to $360^{\circ }$. We’re clearly given two of these angles as $24^{\circ }$, but what about the others?

Well, the only other piece of information we have is $x$. All circles have $360^{\circ }$, which means that we can find the big obtuse angle B by doing $360$ minus the small acute angle $x$. So that’s three of the angles we need. The fourth angle is the one created by the rightmost point on the circle, and using the central angle theorem, we know this will be $x/2$. Putting all this together, we get the equation:

$$\begin{array}{rl}24+24+(360-x)+x/2& =360\\ 24+24+360-x+x/2& =360\\ 24+24-x+x/2& =0\\ 48-x+x/2& =0\\ 48-x/2& =0\\ 48& =x/2\\ 96& =x\end{array}$$

Knowing that $y=88$ and $x=96$, we have our answer that Quantity B must be greater than Quantity A.