Factorization of quadratics and cubics | Intermediate algebra | ACT Math

In this chapter we will factor both quadratic and cubic functions. Cubic functions are much less common, but you will still need to know how to factor them in some special cases.

Factoring quadratic functions

The highest exponent on a variable in a quadratic function is $2$ . The way we factor this type of function is by forming two sets of parentheses that, when multiplied together, result in our original function. By doing this, we factor the function. Let’s see how this works

Format

$(x + 2) (x - 1)$

This is a good example of a quadratic factorization. To be clear, this is what you end up with after you factor the function. Now, in order to multiply two sets of parentheses together, we have to FOIL. If you are unfamiliar with this method of multiplication, please review the chapter Simplifying Expressions. By FOILing, we end up with the equation:

$x^{2} - x + 2 x - 2$

This simplifies to:

$x^{2} + x - 2$

As you can see, factoring a quadratic equation is simply the opposite of FOILing. The factorization of a quadratic equation will be in the form $(x + a) (x + b)$ where the addition can instead be subtraction.

Method

We need to perform two major steps to factor a classic quadratic equation. First, we need to take the third number, the number without an $x$ on it, and determine the factors of it. Then, we will add together those factors to see if the sum equals the second number, the number with $x$ attached to it. In other words, the sum of the factors of the third number in the equation must equal the second number in the equation. After we find the correct factors, we make them the numbers within the parentheses. Let’s walk through an example.

$x^{2} + 5 x + 6$

What are the factors of the third number?

The factors of $6$ are $1 * 6$ and $2 * 3$

Which of these factor sets adds up to the second number?

$1 + 6 = 7$ This one does not add up to 5.

$2 + 3 = 5$ This one does indeed add up to the second number!

So, we have determined that the correct factors are $2$ and $3$ .

Now, let’s set up the parentheses.

To set up the parentheses of the factorization, place an $x$ on the left-hand side of each set, then put the factored numbers on the right-hand side of the sets. It is not important which number goes into what set of parentheses. Something to be sure of is whether the factored number is positive or negative. If the number you are putting on the right-hand side of the parentheses is negative, use a subtraction sign. If the number is positive, use an addition sign. Let’s finish up our example.

Place an $x$ on the left-hand side of each set of parentheses:

$(x +) (x +)$

Now fill in the right-hand side with our factors from the third number, $2$ and $3$ :

$(x + 2) (x + 3)$

That is the final answer!

Note that $(x + 3) (x + 2)$ is also a valid answer.

Try an example with a negative in the equation.

Factor the following equation.

$x^{2} + 2 x - 8$

(spoiler)

Factors of the third number: $- 1 * 8$ , $1 * - 8$ , $- 2 * 4$ , $2 * - 4$

Find the factors that sum up to second number:

$- 1 + 8 = 7$

$1 + - 8 = - 7$

$- 2 + 4 = 2$

These are the correct factors.

Set up parentheses: $(x +) (x +)$

Place numbers, being mindful of the negative sign on $- 2$ , to get the final answer:

$(x - 2) (x + 4)$

Remember, you can always check to see if your factorization is correct by FOILing the parentheses and seeing if you get the original quadratic equation.

Factoring cubic equations

A cubic function may be identified by its highest exponent on a variable being $3$ . In order to factor a cubic equation, you must be given one of the factors beforehand. Your resulting factorization of a cubic equation will not be sets of parentheses. Instead, it will be a quadratic function. So, you factor a cubic function by breaking it down to a quadratic function. At that point, you can follow the above steps for factoring quadratic equations to get the final factorization of the cubic function if asked to do so.

Many factorizations of cubic functions will require you to perform synthetic division. If you are unfamiliar with synthetic division, the section below will provide a brief overview. If you are comfortable performing synthetic division, feel free to skip the next section in this chapter and get right to the method. You can also use long division, but, as you may have guessed, long division takes longer! On the ACT, we don’t really have time to take longer on anything, so learning synthetic division is highly recommended.

Synthetic division

For this explanation, we will be using the equation $2 x^{3} + 6 x^{2} - 17 x + 15$ and the given factor needed to solve the problem, $x + 5$ . Follow the detailed instructions below. In the graphics, blue arrows represent the movement of a number and the red arrow represents the multiplication of the two numbers involved.

$\frac{( 2 x ^{3} + 6 x ^{2} - 17 x + 15 )}{( x + 5 )}$

First, list the coefficients of the original equation (use $0$ s as placeholders if there is no term for a given exponent).

Next, drop the first coefficient down below the line:

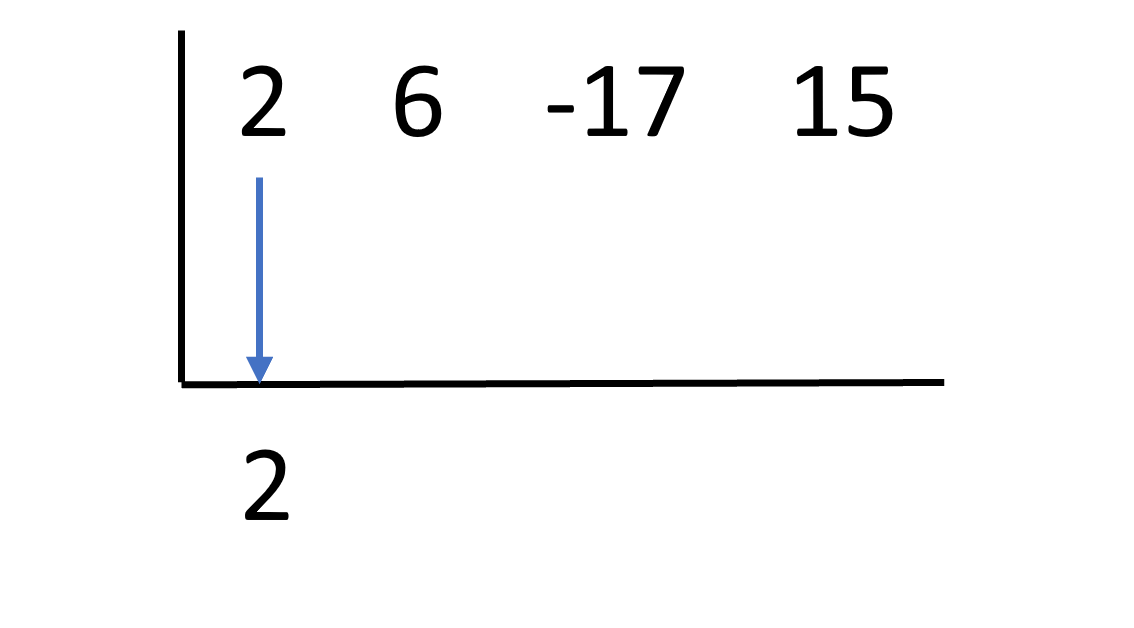
$Example of the first step in synthetic division$

Now, take the root from the factor you are given and place it to the left of the vertical line. In this case, the number is $- 5$ . This was obtained by setting $(x + 5) = 0$ and solving for $x$ . If you are confused about this, revisit the chapter “Solving quadratic equations.”

Then, multiply the root number ( $- 5$ ) by the first number under the line ( $2$ ). This equals $- 10$ .

Next, put this number underneath the second coefficient.

Add this number ( $- 10$ ) to the coefficient above it and place the sum ( $- 4$ ) under the line.

Now, repeat this step for the rest of the coefficients.

Multiply that sum ( $- 4$ ) by $- 5$ and place it ( $20$ ) under the third coefficient.

Add the number ( $20$ ) and the number above it and place the sum under the line.

Multiply that sum ( $3$ ) by the root number ( $- 5$ ) and place it ( $- 15$ ) under the fourth coefficient.

Lastly, place the sum of that number ( $- 15$ ) and the number above it under the line.

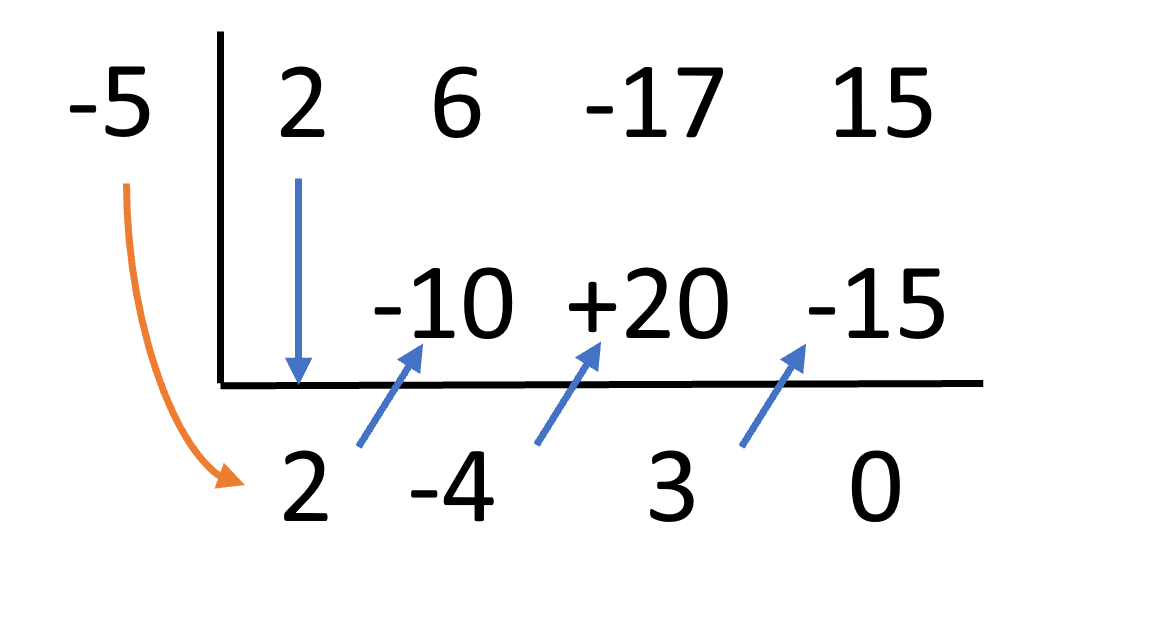
$Example of synthetic division$

After performing this pattern for the whole equation, it will result in a new number beneath the line under each coefficient. The most important part is that the last number (this is the remainder) should be $0$ ! If it’s not $0$ , redo the synthetic division to ensure you did it right. If you did it right, and it’s not zero, then the root that you used is not a factor of the cubic equation and you cannot continue factoring. These numbers below the line are the coefficients of the new, reduced equation. You began with a cubic function, so our resulting function will be quadratic. We decrease by one exponent of power. So, the final result is:

$2 x^{2} - 4 x + 3$

Method

To factor a cubic function, we will begin by dividing our cubic equation by the factor we are given. An example question could look like the following.

Factor the cubic equation $x^{3} - 8 x + 3$ given that $(x + 3)$ is one of the factors.

You will perform synthetic division to reduce the cubic function to a quadratic function, as done in the above section. Then, simply factor the quadratic function received as a result of the synthetic division. You will end up with two sets of parentheses in addition to the factor given to you in the problem, and all three of them together make up the factorization of the cubic equation.

Sum or difference of two cubes

You can quickly factor a cubic function of the form $a^{3} + b^{3}$ by memorizing the resulting expression

$(a + b) (a^{2} - ab + b^{2})$

This is called the sum of two cubes.

Similarly, you can quickly factor a cubic function of the form $a^{3} - b^{3}$ by memorizing the result expression

$(a - b) (a^{2} + ab + b^{2})$

This is called the difference of two cubes.

Key points

Factoring quadratic functions. This is the opposite of FOILing two sets of parentheses. The factors of the third coefficient should sum to equal the second coefficient. Place $x$ to the left-hand side of each set of parentheses and the factors of the third coefficient to the right-hand side of the parentheses.

Synthetic division. Divide a cubic function by a smaller polynomial to reduce the function to a quadratic.

Factoring cubic functions. Perform synthetic division with the factor given by the problem, then factor the quadratic function that results from the division.

Sum of two cubes. With a cubic equation of the form $a^{3} + b^{3}$ , factor it to the form: $(a + b) (a^{2} - ab + b^{2})$

Difference of two cubes. With a cubic equation of the form $a^{3} - b^{3}$ , factor it to the form: $(a - b) (a^{2} - ab + b^{2})$