Work, energy, periodic motion, wave characteristics | Translational motion, forces, work, energy, and equilibrium | Chem/phys

Energy of point object systems

Work and energy are interchangeable concepts, with all forms of energy measured in Joules. One key form is kinetic energy, defined by the equation

$K E = \frac{1}{2} m v$

where $m$ represents mass and $v$ represents speed.

This formula shows that the energy unit is equivalent to $kg \cdot m^{2} / s^{2}$ . For a constant speed, increasing the mass results in proportionally higher kinetic energy—for instance, doubling the mass doubles the kinetic energy.

Conversely, for a fixed mass, increasing the speed has an even greater effect; doubling the speed quadruples the kinetic energy since speed is squared. This demonstrates that variations in speed have a more dramatic impact on kinetic energy than equivalent changes in mass.

Potential energy (PE)

Potential energy is the energy stored in an object due to its position or configuration.

Near Earth’s surface, gravitational potential energy is given by $PE = m g h$ , where $m$ is mass, $g$ is the acceleration due to gravity, and $h$ is the height above the ground. This expression is considered local because it applies specifically to Earth’s gravitational field, where $g \approx 9.8 m/ s^{2}$ , though it varies on other planets with different mass-to-radius ratios.

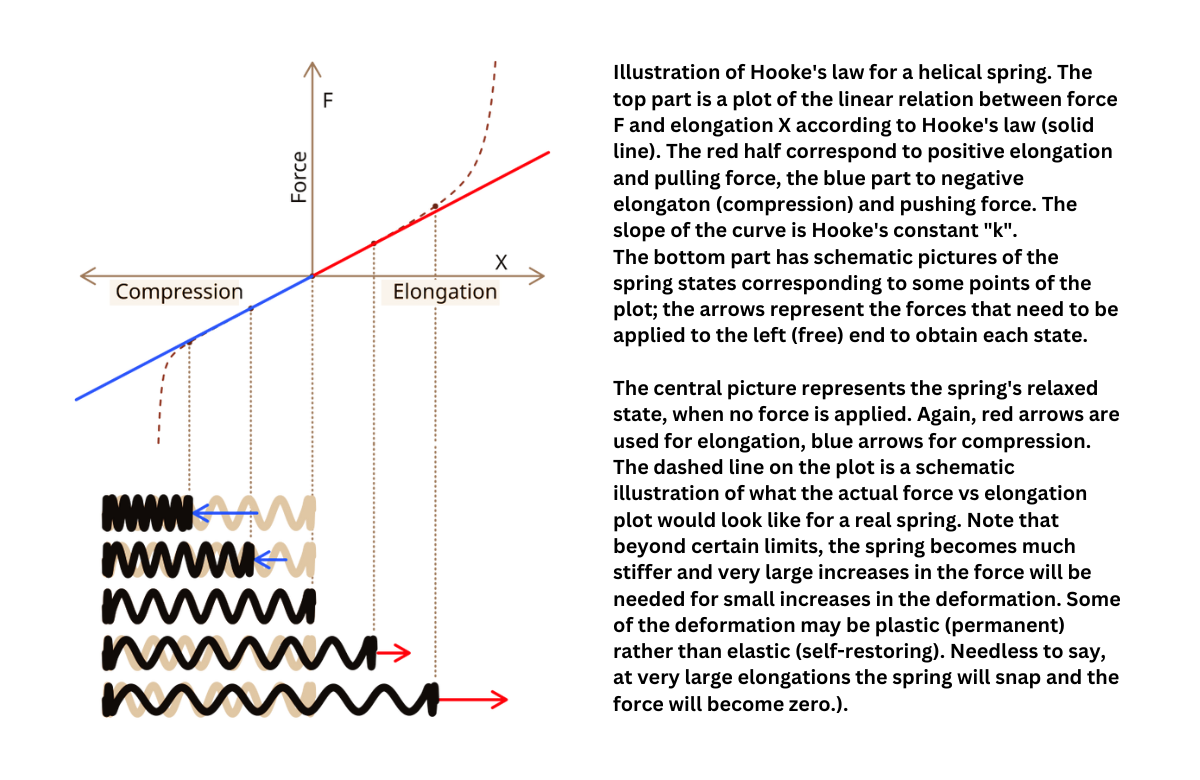
For elastic systems, the energy stored in a spring is expressed as $PE = \frac{1}{2} k x^{2}$ , where $k$ is the spring constant and $x$ is the displacement from equilibrium. A larger $k$ indicates a stiffer spring that requires more energy to stretch or compress.

In a broader context, the general formula for gravitational potential energy between any two masses is $PE = - \frac{G m M}{r}$ , where $G$ is the universal gravitational constant, $m$ and $M$ are the masses involved, and $r$ is the distance between their centers.
The negative sign signifies that work is required to separate the masses against the gravitational force.

Conservation of energy

Conservation of energy means that the total energy in an isolated system remains constant—what you start with is what you end with. For example, as an object falls, its gravitational potential energy is converted into kinetic energy, but the overall energy remains unchanged. Similarly, when a crate slides to a stop on a rough surface, its kinetic energy is transformed into heat and sound energy, yet the total energy is conserved.

Power, units

Power is the rate at which energy is used or transferred over time. It is measured in Watts, which are equivalent to Joules per second. This means that accomplishing the same amount of work in a shorter period, like lifting a crate in one minute, requires a higher power output than doing it over an hour.

Periodic motion

Amplitude, frequency, phase

Periodic motion involves repeating cycles that can be described using amplitude, period, and frequency. The amplitude ( $A$ ) is the maximum displacement of a wave from its equilibrium position, representing how high the peaks or how low the troughs extend, and is measured in meters. A larger amplitude indicates that the system possesses more energy.

The period ( $T$ ) is the time required for one complete cycle of the motion, measured in seconds, and it is inversely related to the frequency ( $f$ ), which is the number of cycles occurring per second, expressed in Hertz ( $Hz$ ). In some cases, frequency may also be given in revolutions per minute ( $r p m$ ), calculated by multiplying the cycles per second by $60$ .

Additionally, angular frequency ( $ω$ ) defines the rate of rotation in radians per second, given by $ω = 2 π f$ , and is also known as angular velocity.

Hooke’s Law

$F = - k x$
The restoring force exerted by a spring, where $k$ is the spring constant (a measure of stiffness) and $x$ is the displacement from the equilibrium position.
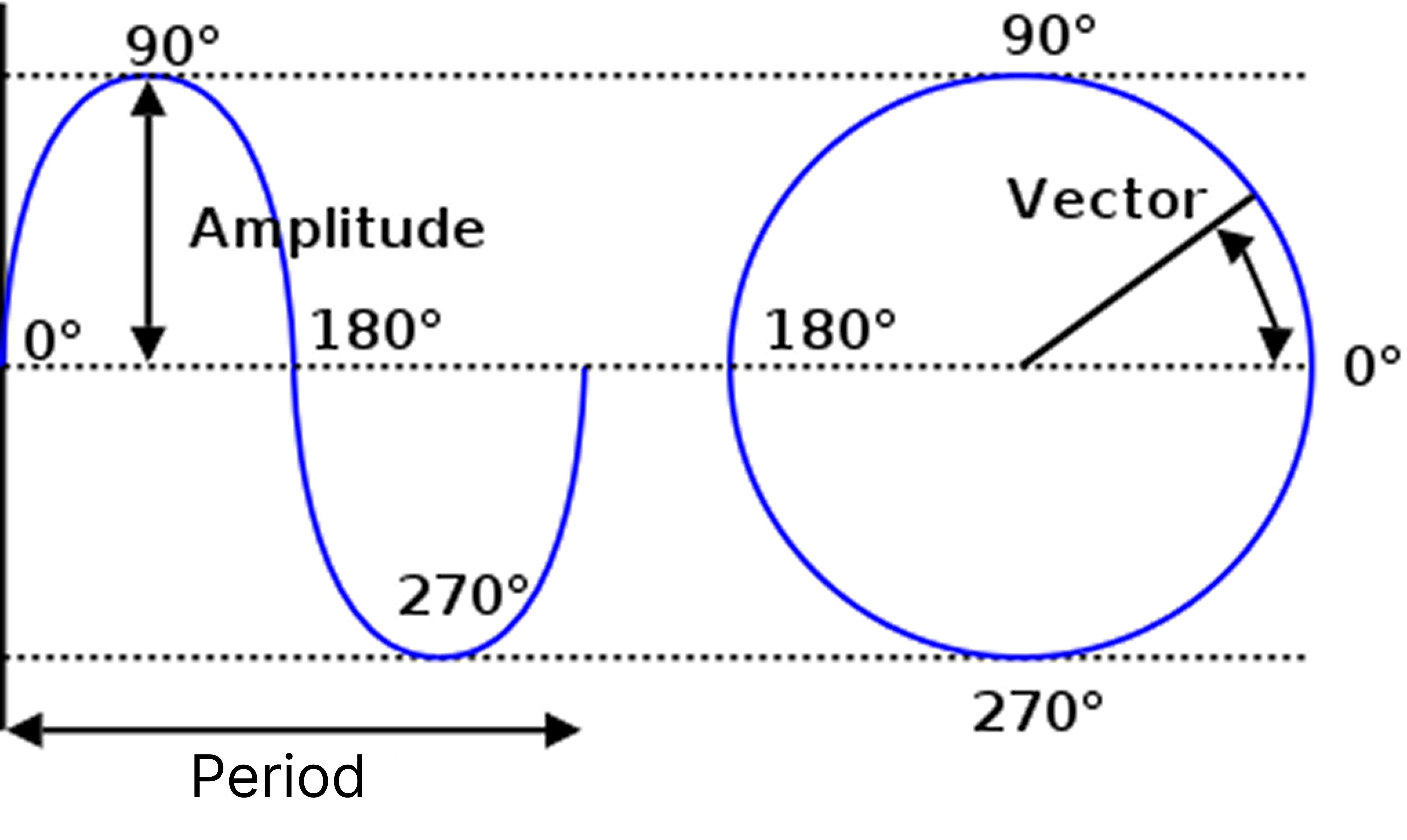
The maximum displacement, or amplitude, is represented by $A$ .

The energy stored in the spring as a result of its deformation is its potential energy ( $PE$ ), calculated as $PE = \frac{1}{2} k x^{2}$
The kinetic energy ( $K E$ ) of a moving mass is given by $K E = \frac{1}{2} m v^{2}$

At the equilibrium position ( $x = 0$ ), the potential energy is zero and the kinetic energy reaches its maximum value.

Conversely, at maximum displacement ( $x = A$ ), the potential energy is at its peak and the kinetic energy is zero.
Throughout the motion, the sum of potential and kinetic energy remains constant, equal to the maximum energy ( $\frac{1}{2} k A^{2}$ ), demonstrating the conservation of mechanical energy.

Hooke’s law: force vs. elongation with spring illustrations

Simple harmonic motion describes a periodic oscillation where the displacement of an object from its equilibrium position varies sinusoidally with time.

This motion can be expressed mathematically as

$x = A \cdot sin (ω t)$

where $A$ is the amplitude—the maximum displacement—and $ω$ is the angular frequency, which is sometimes also called angular velocity.

Common examples of this type of motion: the oscillation of a spring, the swinging of a pendulum, and the projection of uniform circular motion onto one axis, which results in a sinusoidal pattern over time.

Spring-mass system

In a spring-mass system, the period ( $T$ ) of oscillation is given by

$T = 2 π \sqrt (m / k)$

where $m$ represents the mass attached to the spring and $k$ is the spring constant.

This equation indicates:

A heavier mass increases the period
A stiffer spring (with a larger $k$ ) decreases it.

Alternatively, the system’s motion can be described using the angular frequency ( $ω$ ), expressed as $ω = \frac{k}{m}$ . A higher angular frequency means the spring vibrates more rapidly, which happens when the spring is stiffer or the attached mass is smaller.

Pendulum motion

The period ( $T$ ) of a simple pendulum is given by $T = 2 π \frac{L}{g}$ where $L$ is the length of the string and $g$ represents gravitational acceleration (approximately 9.8 $m / s^{2}$ ).

Alternatively, the motion can be characterized by its angular frequency ( $ω$ ), defined as $ω = \frac{g}{L}$ . This means that a pendulum swings faster when the gravitational force is stronger or when the string is shorter.

General periodic motion: velocity, amplitude

In periodic motion, the sum of potential energy and kinetic energy remains constant.

At the equilibrium position, where displacement is zero, the potential energy is zero and the kinetic energy is at its maximum ( $\frac{1}{2} m v^{2}$ ).
Conversely, at maximum displacement—known as the amplitude ( $A$ )—the kinetic energy drops to zero while the potential energy is at its peak.

For a spring, this maximum potential energy is $\frac{1}{2} k A^{2}$ .

For a pendulum, it is $m g A$ , with $A$ representing the maximum height achieved during the swing.

By equating the maximum kinetic energy to the maximum potential energy, one can determine the amplitude from the equilibrium velocity, or vice versa.

Wave characteristics

Transverse and longitudinal waves: wavelength and propagation speed

A transverse wave is one where the displacement of the medium occurs perpendicular to the direction of propagation. This is typical of electromagnetic radiation such as light, and can be observed in a standing wave on a string, where the speed depends on the square root of the string tension divided by the mass per unit length—meaning that stiffer, lighter strings yield faster waves.

Conversely, a longitudinal wave features displacement that is parallel to the direction of travel. This type of wave is characteristic of sound, pressure waves, and seismic vibrations produced during earthquakes.

Wavelength, frequency, and velocity

Wavelength, frequency, velocity are related by the equation

$v = f λ$

where $v$ is the speed of the wave, $f$ (sometimes denoted as $ν$ ) is the number of oscillations per second measured in Hertz, and $λ$ is the distance between successive wave peaks measured in meters.

Amplitude, intensity

The amplitude of a wave indicates its maximum displacement from equilibrium and is* directly linked to the energy carried by the wave*—greater amplitude means higher energy.
Intensity quantifies the energy transmitted per unit area per unit time, essentially representing the power per area, so an increase in amplitude typically leads to a higher intensity.

For electromagnetic waves such as light, while increased amplitude and intensity boost the overall energy of the wave, they do not alter the energy per photon, which depends solely on the wavelength; shorter wavelengths (or higher frequencies) result in photons with more energy.

Superposition of waves, interference, addition

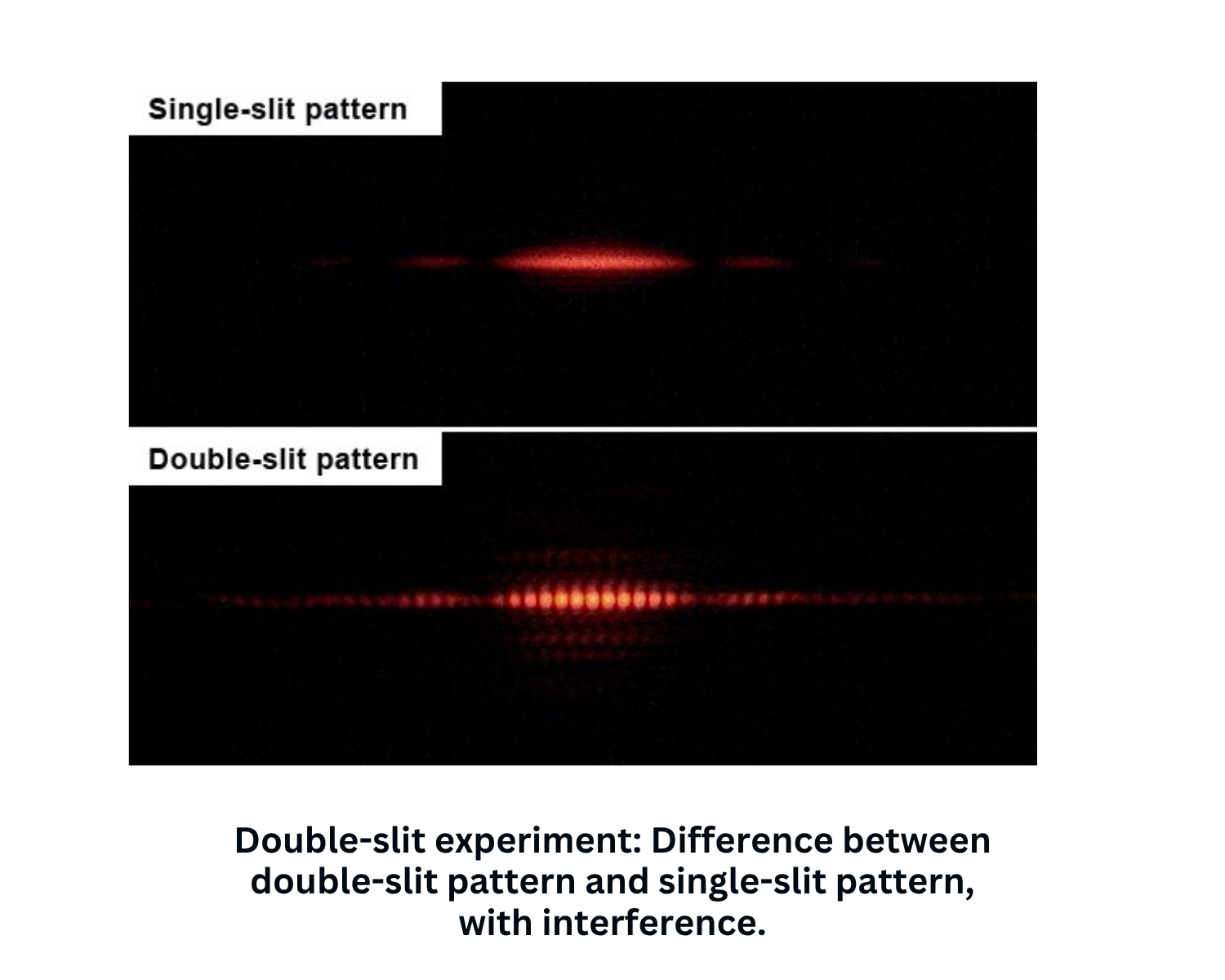
Superposition occurs when multiple waves overlap, causing them to combine through wave addition. This overlapping results in interference, which can either amplify or diminish the overall wave amplitude.

When waves are in phase, meaning their peaks and troughs align, they produce constructive interference and the amplitude increases.
Conversely, when waves are out of phase, with peaks aligning with troughs, destructive interference takes place, reducing the amplitude or even canceling the waves.

Resonance

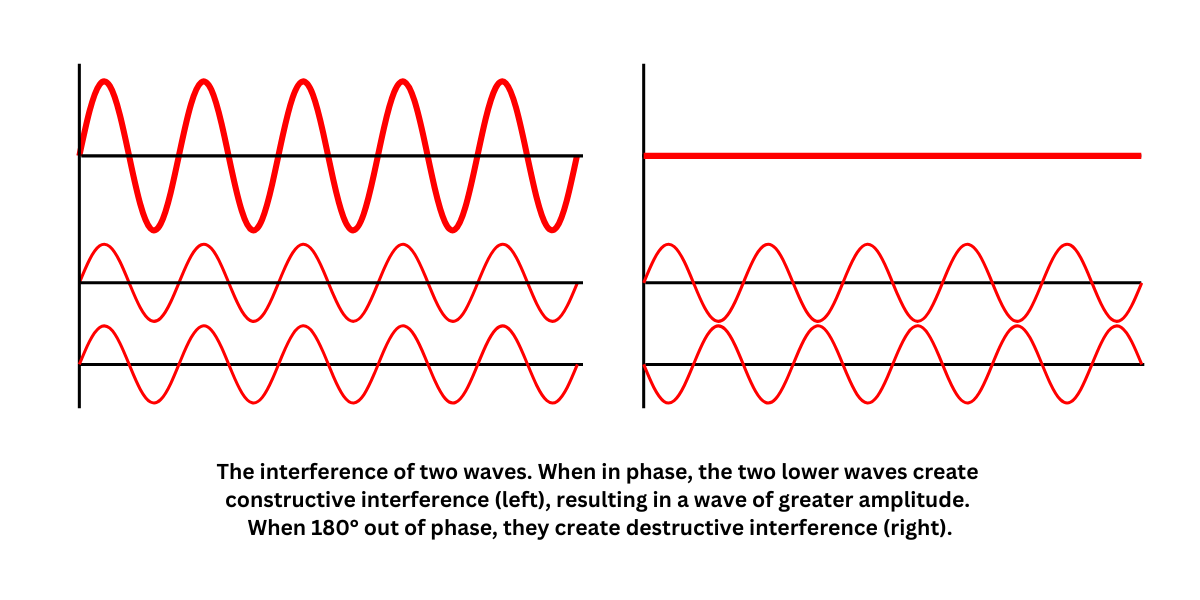
Resonance occurs when an oscillating system reaches its maximum amplitude, typically when driven at specific resonance frequencies. For example, when a string or tube vibrates at one of these frequencies, it produces standing waves that exhibit high amplitude.

These resonance frequencies can be determined using the relationship

$f = v / λ$

where $f$ is the frequency, $v$ is the speed of the wave, and $λ$ is the wavelength.

In systems like strings or tubes that are open at both ends, the condition is $L = n /2 λ$
In tubes with one closed end, it is $L = n_{0} dd /4 λ$ , with $L$ representing the length of the medium and $n$ or $n_{0} dd$ the harmonic number.

Standing waves formed at resonance do not travel; instead, they remain fixed in place, characterized by nodes, which are points of no oscillation, and antinodes, where oscillation is at its maximum.

Beats

When two waves of slightly different frequencies interfere, beats occur. The beat frequency is simply the difference between the two frequencies, producing periodic fluctuations in amplitude.

Refraction and diffraction

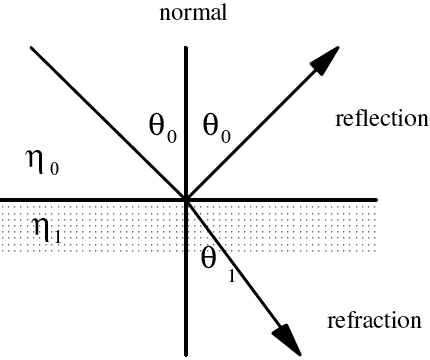
Refraction is the bending of waves as they pass between different media. It is governed by Snell’s law:

$n_{1} s in θ_{₁} = n_{2} s in θ_{2}$

where $n$ represents the refractive index and $θ$ is the angle measured from the normal.

When light enters a denser medium, it bends toward the normal. A specific form of refraction, known as dispersion, occurs when light is separated into its component colors by a prism or water droplets, creating a rainbow.

Diffraction is the phenomenon where waves spread out as they encounter obstacles or pass through narrow openings. This diffusion of energy causes effects such as sound being heard around corners and light forming a diffuse pattern rather than a sharp dot when passing through a small aperture. Diffraction is also the basis for interference patterns observed in single and double slit experiments.