Force

There are four fundamental forces:

• The strong force—also known as the nuclear force—is the most powerful, yet it acts only over subatomic distances to bind nucleons together.
• The electromagnetic force is about one order of magnitude weaker but operates over much larger distances, holding atoms together and enabling phenomena such as magnets sticking to refrigerators.
• The weak force is roughly ten orders of magnitude less potent than the strong force and plays a key role in radioactive decay.
• Gravity is about fifty orders of magnitude weaker than the strong force, governing weight and controlling the orbits of planets.

Center of mass

The center of mass is the weighted average of all positions, where each position is scaled by its mass. In a Cartesian system, this means calculating a weighted average of the x, y, and z coordinates to locate the point where the entire mass of the object or system is balanced. For instance, in a system comprising the Earth and a small chicken, the center of mass lies almost entirely within the Earth due to the chicken’s negligible mass. Conversely, for two equally massive chickens, the center of mass will be exactly midway between them. Absolute coordinates are unnecessary when determining the center of mass; any reference point can be used to establish relative coordinates. Additionally, for symmetric objects like a sphere or an inner tube, the center of mass is located at the geometric center.

Newton’s Laws

Newton’s First Law, inertia

Newton’s first law, also known as the law of inertia, states that an object will continue in its current state of motion unless acted upon by an external force. In other words, if an object is at rest, it will remain at rest, and if it is moving, it will maintain its speed and direction unless a force causes it to change. Essentially, objects inherently resist any alterations in their motion.

Newton’s Second Law ($F=ma$)

Newton’s second law, expressed as $F=ma$, states that a net force acting on an object causes it to accelerate in the direction of that force. The standard unit of force is the Newton ($1N=1kg\cdot m/s^2$). Both force and acceleration are vectors, meaning they possess both magnitude and direction.

Newton’s Third Law, forces equal and opposite

Newton’s third law states that for every applied force, there is a reaction force (counterforce) that is equal in magnitude (strength) and opposite in direction.

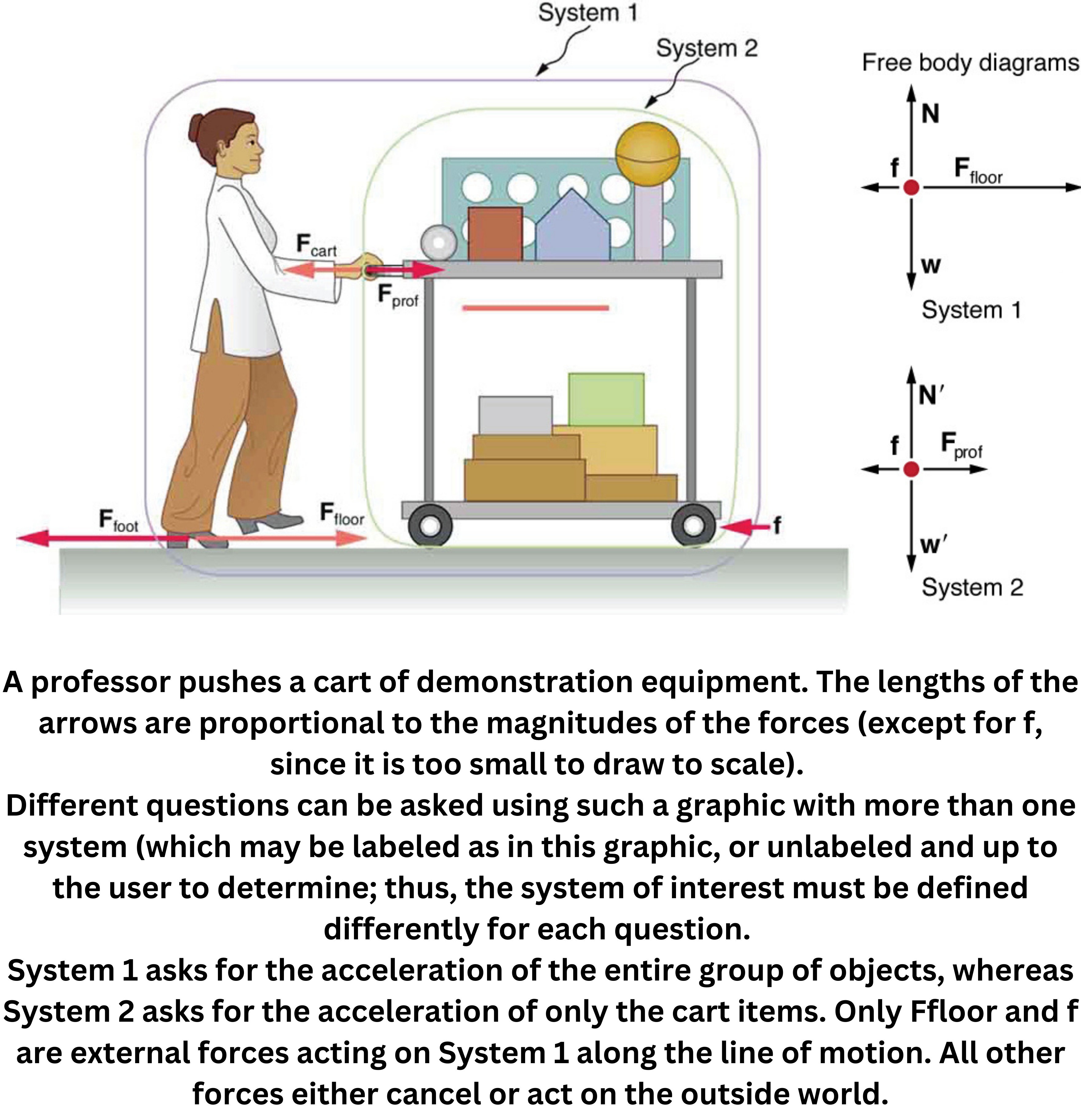
Forces inherently occur in pairs, meaning an object cannot apply force without also receiving a corresponding reaction. This principle, often summarized as action-reaction, is crucial for analyzing the origin of forces and identifying which forces act externally on a system.

Fields

A field is often represented by lines that illustrate both its strength and direction. When these lines are close together, the field is strong; when they are far apart, the field is weak. Because these lines possess a specific direction, they act as vectors. Consequently, objects may travel parallel to, perpendicular to, or in a spiral path along these field lines.

Uniform circular motion

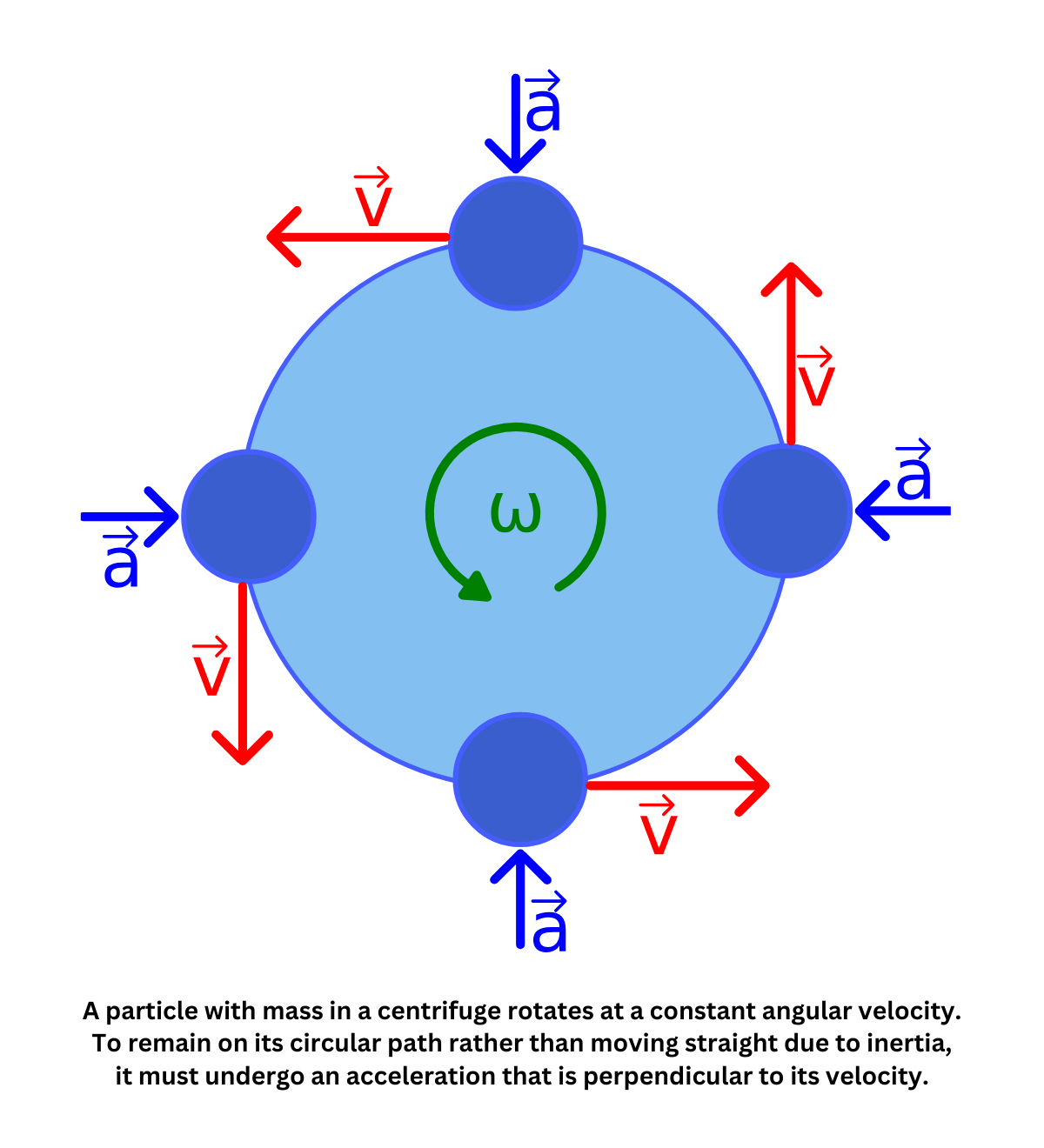
Uniform circular motion is the simplest form of curved motion in which an object moves along a circular path at a constant speed. Even though its speed remains unchanged, its velocity continuously changes direction, resulting in centripetal acceleration. This acceleration is produced by a net external force known as the centripetal force, which is the total of all forces acting on the object to keep it moving in a circle.

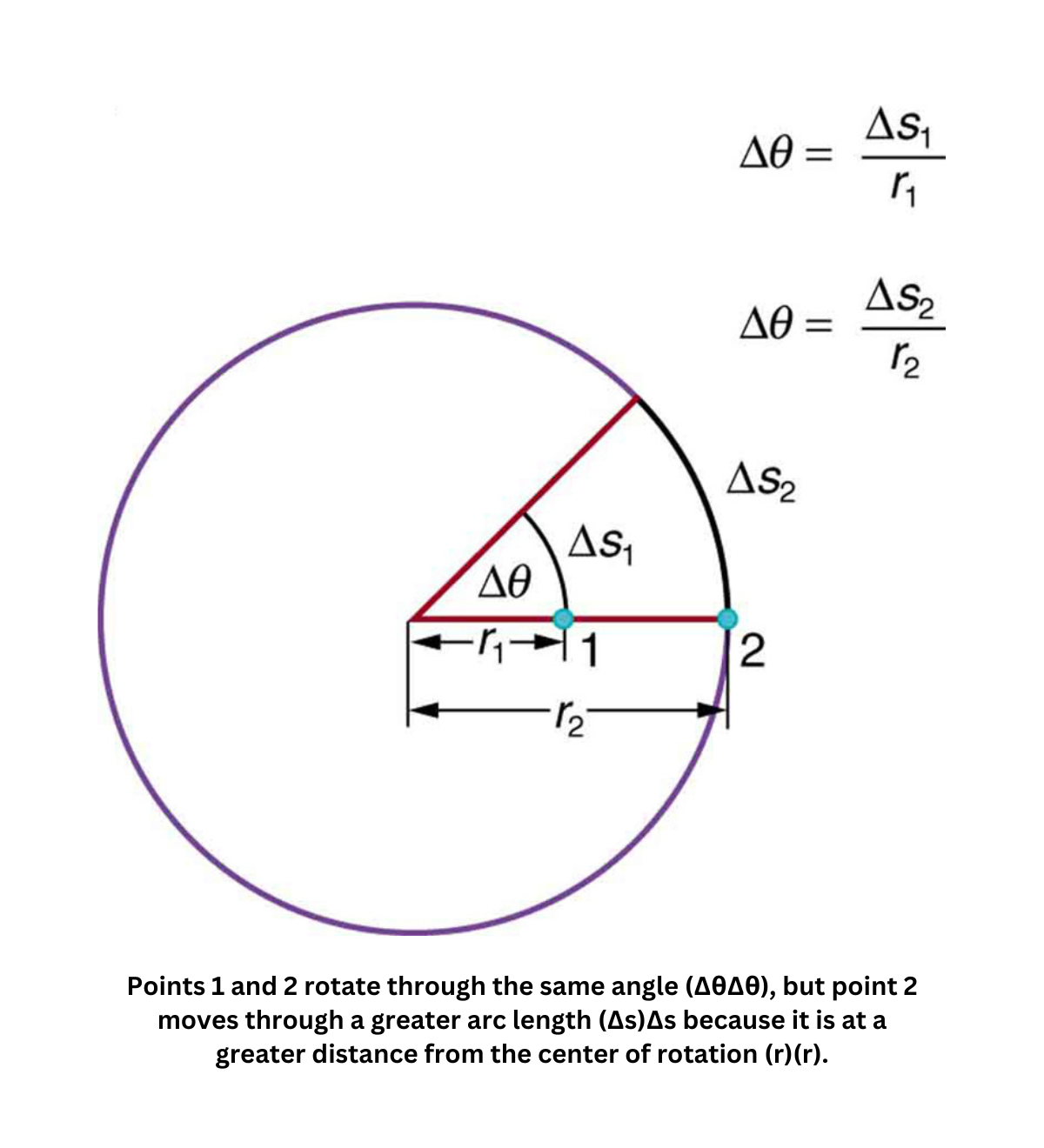
Rotation angles are measured in radians ($rad$), where $2\pi rad$ corresponds to one full revolution. In this context, the arc length ($\Delta$$s$) represents the distance traveled along the circular path, and the radius ($r$) is the distance from the center of the circle to any point on the path. For one complete revolution, the arc length equals the circumference of the circle, calculated as $2\pi$$r$, which confirms that the rotation angle $\theta$ is $2\pi$.

Angular velocity ($\omega$)

Angular velocity is defined as the rate at which an angle changes, mathematically expressed as

$$\omega =\frac{\Delta \theta }{\Delta t}$$

where $\Delta \theta$ is the angular displacement over the time interval $\Delta t$. A larger $\Delta \theta$ in a fixed time results in a higher angular velocity, measured in radians per second ($\text{rad/s}$).

This concept parallels linear velocity ($v$), which describes the rate at which an object moves along a path. For instance, a point on a fan blade travels an arc length ($\Delta s$) in time $\Delta t$, giving it a linear velocity:

$$v=\frac{\Delta s}{\Delta t}$$

Because the arc length is related to the angular displacement by $\Delta s=r\Delta \theta$, where $r$ is the radius, substituting into the linear velocity formula yields:

$$v=r\frac{\Delta \theta }{\Delta t}$$

or equivalently,

$$v=r\omega$$

Centripetal acceleration

When an object moves in a circular path at constant speed, its instantaneous velocity is always tangent to the path, even though its speed remains unchanged. This constant change in direction results in an acceleration directed toward the center of the circle, known as centripetal acceleration. This acceleration arises because the velocity vector is continuously changing, and its magnitude can be determined by analyzing the geometry of the motion.

By comparing the triangle formed by the velocity vectors at two nearby points with the triangle defined by the radius ($r$) and the arc length ($\Delta$s), we find that the change in velocity ($\Delta$v) is proportional to the product of the speed ($v$) and the arc length divided by $r$.

Dividing $\Delta v$ by the time interval ($\Delta t$) gives us the acceleration, so that:

$$a_c=\frac{v^2}{r}$$

Consequently, higher speeds or smaller radii result in greater centripetal acceleration, which is why navigating a sharp curve at high speed requires significantly more force.

Any net force that produces uniform circular motion is known as a centripetal force. This force is directed toward the center of curvature, which is the same direction as the centripetal acceleration. According to Newton’s second law ($F=m\cdot a$), the net force on an object equals its mass multiplied by its acceleration.

In the case of uniform circular motion, the acceleration is the centripetal acceleration, so the magnitude of the centripetal force is given by:

$$F_c=m\cdot a_c$$

Weight

The equation for weight is $w=mg$, representing the gravitational force acting on a mass $m$. On Earth, where the acceleration due to gravity $g$ is $9.80{\text{ m/s}}^2$, a 1.0 kg object weighs:

$$w=mg=(1.0\text{ kg})(9.80{\text{ m/s}}^2)=9.8\text{ N}$$

When an object is at rest on a horizontal surface, the normal force exactly balances its weight.

On an inclined plane, the normal force and friction force combine as vectors to counteract the weight.

Friction, static and kinetic

Friction is the force that resists relative motion between surfaces in contact. It acts parallel to the surface, always opposing any actual or attempted movement. When two surfaces slide past one another, this resistance is known as kinetic friction, such as when a shopping cart slows when rolling across a flat parking lot. Conversely, if the surfaces remain stationary, static friction comes into play, typically providing a greater force than kinetic friction to prevent motion.

Static friction is always greater than kinetic friction; correspondingly, the coefficient of friction for static friction exceeds that for kinetic friction. This coefficient is dependent on the properties of the materials in contact and is determined empirically.

On a horizontal surface, the normal force equals the weight of the object, whereas on an inclined plane the normal force is the weight multiplied by the cosine of the incline angle. Lubricants reduce friction by altering surface properties and lowering the coefficient of friction. Additionally, friction always produces heat as a by-product.

Motion - Inclined Plane

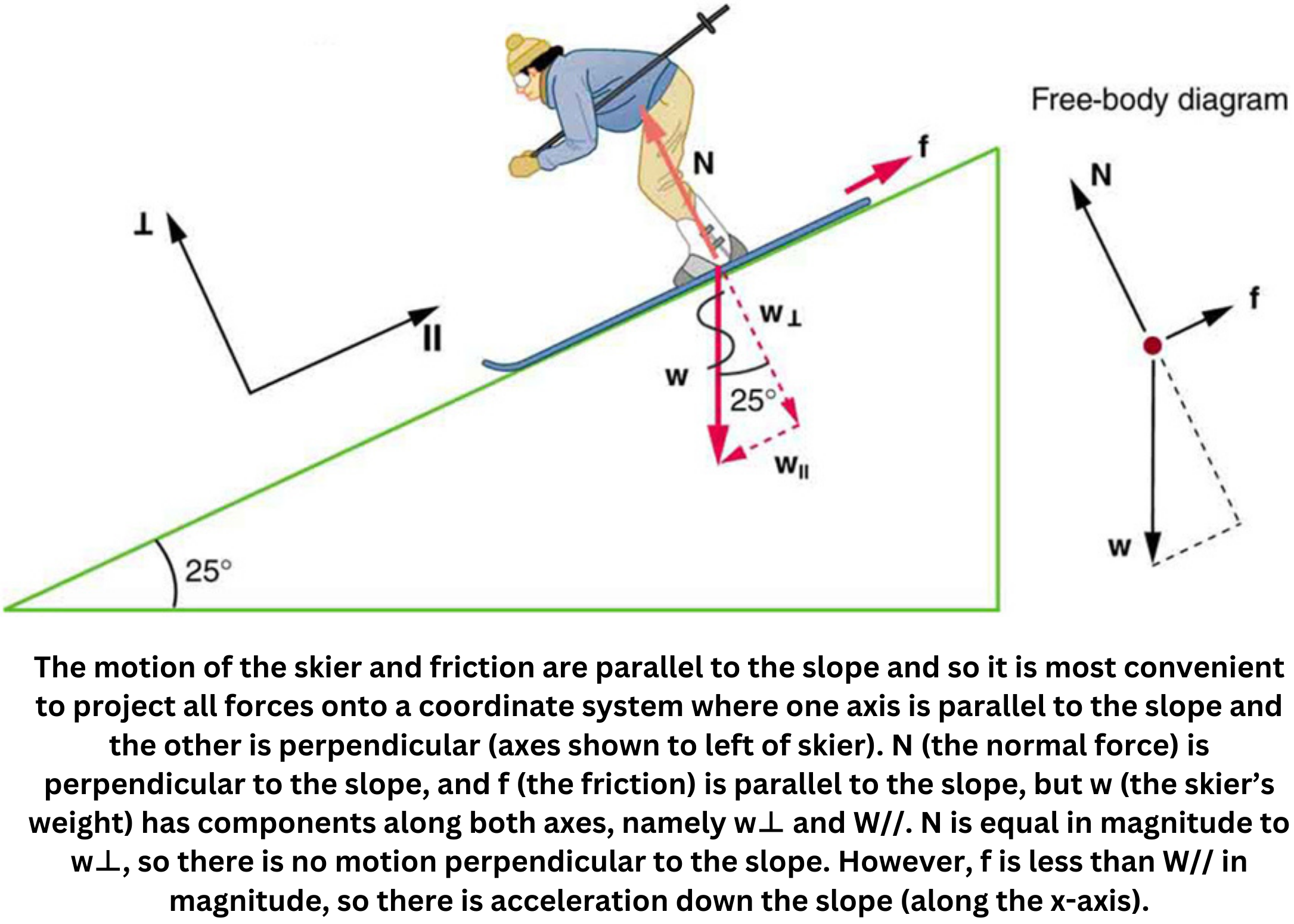
On an inclined plane, gravity is split into two components: one perpendicular to the surface and one parallel to it. The perpendicular component is calculated as:

$$F_N=mg\cdot \cos \theta$$

This component is counteracted by the normal force from the surface, preventing the object from sinking into the plane. The parallel component:

$$F_{\parallel }=mg\cdot \sin \theta$$

is the force that drives the object along the plane.

Friction acts along the surface, opposing any motion. For an object at rest, static friction balances the parallel component of gravity. When the object moves at a constant velocity, the parallel force equals kinetic friction. If the object starts to slip or accelerate, the gravitational pull along the plane exceeds the static or kinetic friction, respectively.

When pushing an object up the incline, the applied force must overcome both the parallel gravitational component and friction. It is important to break this force into its components since only the component parallel to the plane contributes to movement.

Pulleys

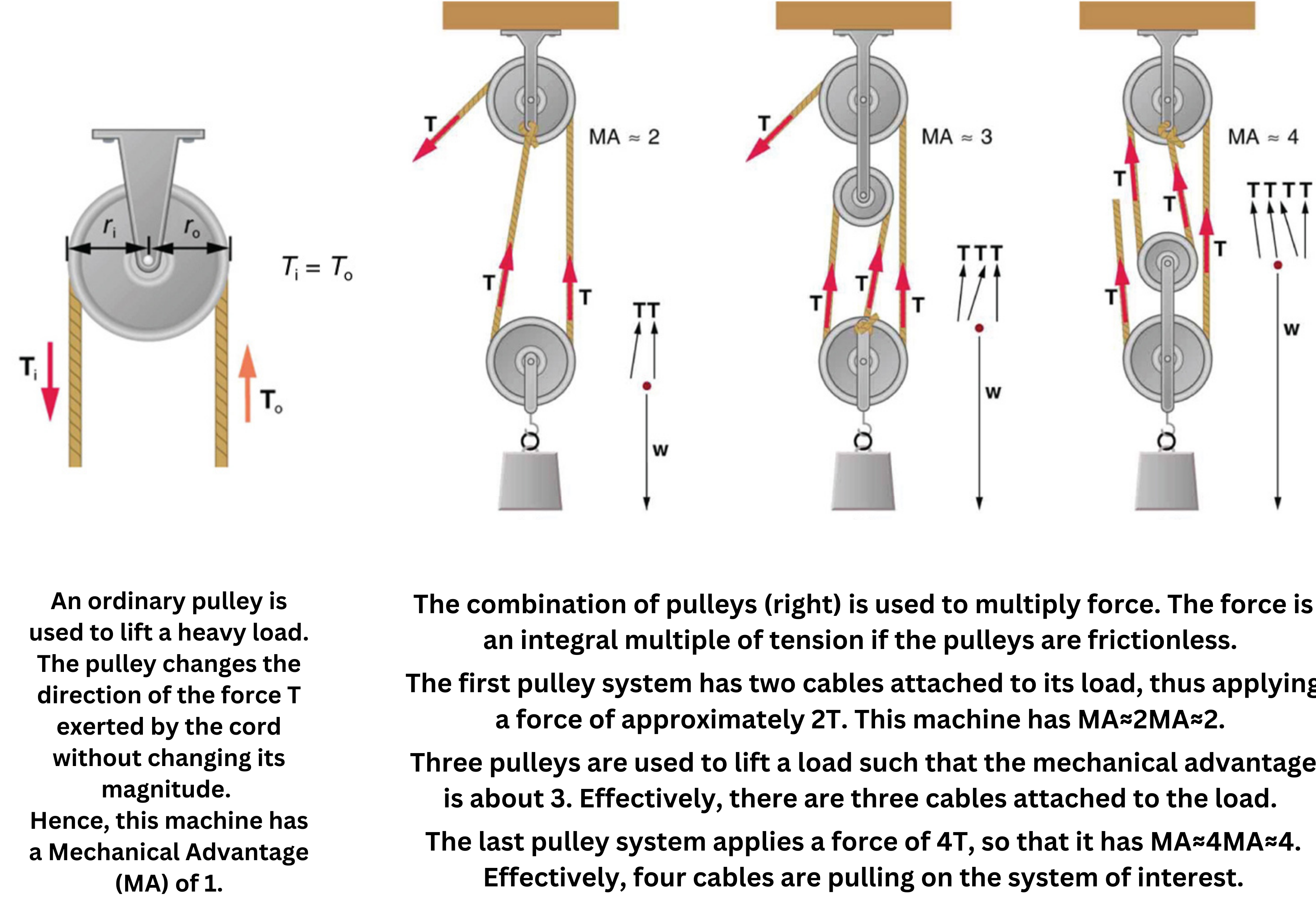
A pulley system reduces the force required to lift an object, though it also increases the pulling distance. Essentially, when a moving pulley is employed, both sides of the rope contribute to lifting the load. In more complex arrangements, additional ropes further reduce the effort, but this benefit comes at the cost of a proportionally longer distance that must be pulled.