Translational motion | 4A: Translational motion, forces, work, energy, and equilibrium | Chem/phys

Units and dimensions

A one-dimensional space involves only a single measure of length or distance.

In a two-dimensional framework, objects are defined on a flat plane using an x-y coordinate system, incorporating both length and width.

Three-dimensional space adds depth, with objects described by x, y, and z coordinates, capturing volume.

Finally, four-dimensional space includes the temporal dimension—time—alongside the three spatial coordinates ( $x, y, z, t$ ), allowing for the depiction of objects as they change over time.

SI units for physics measurements organized by base quantities

Vectors, components

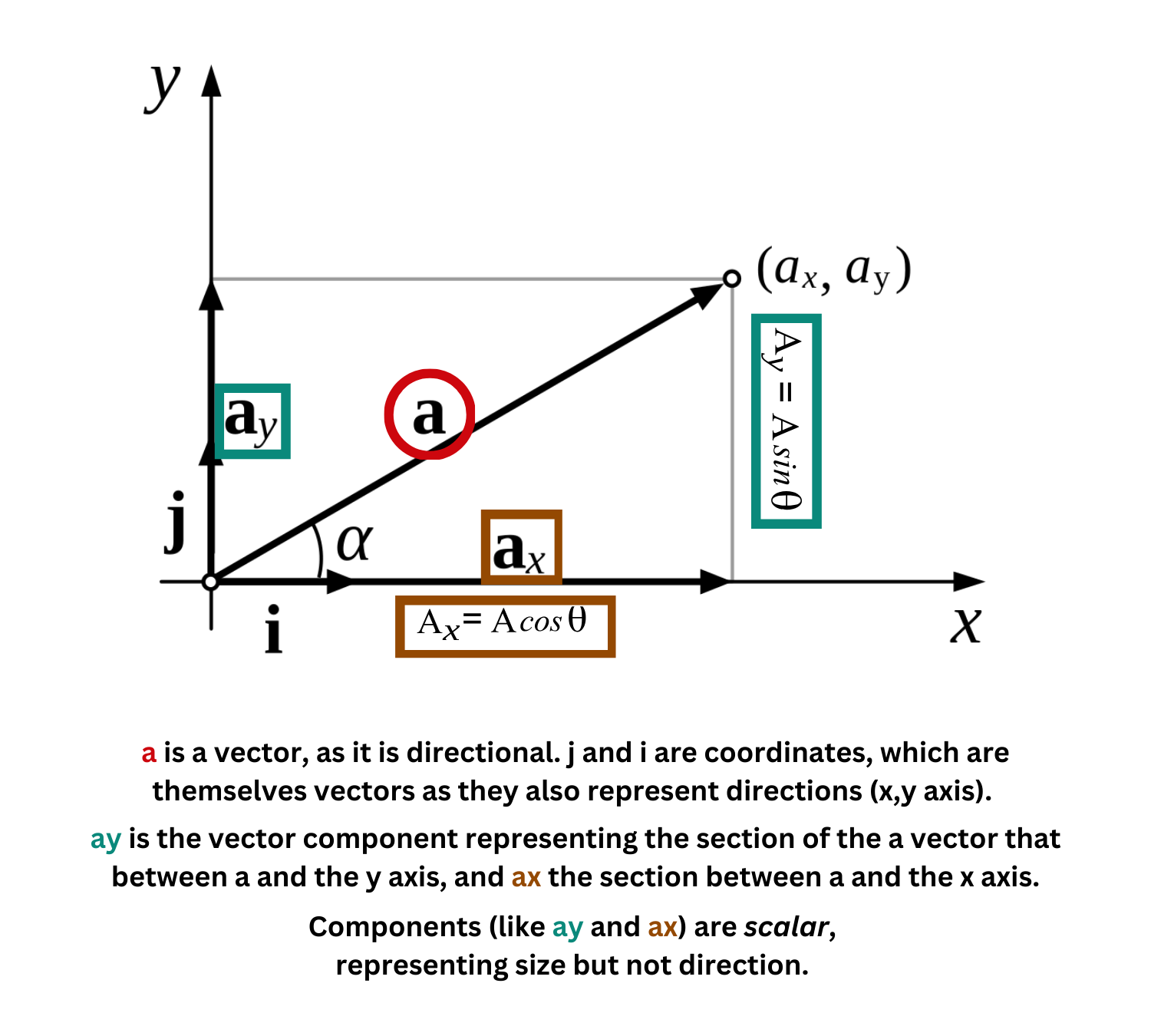
A scalar is a quantity defined solely by its magnitude—such as length, time, or mass—without any directional component.

A vector possesses both magnitude and direction, ex. displacement, acceleration, or force.

The components of a vector are its projections along specific directions or axes, breaking the vector down into parts that represent how much of it acts in each direction. The components represent an amount (how much space falls between the vector and the coordinate) and do not represent a direction themselves, so they are scalar.

A common mnemonic for remembering trigonometric ratios is SOH CAH TOA. Some people like to just sound out the phrase, like “Sock a Toe-a”, while others find it helpful to have a phrase, such as:

Some Old Hippie Caught Another Hippie Tripping on Acid

Either way, this helps us remember that:

sin $θ$ is the ratio of the opposite side to the hypotenuse
cos $θ$ is the ratio of the adjacent side to the hypotenuse,
tan $θ$ is the ratio of the opposite side to the adjacent side.

Vector addition

Vector addition can be performed directly only when vectors share the same direction.

When they differ, you must decompose each into its $x, y$ , and $z$ components and add these components separately to form the resultant vector. In effect, the sum of all the components of a vector reproduces the original vector.

Note that an operation between two vectors may yield either a vector or a scalar (for example, squaring a vector’s magnitude to calculate kinetic energy produces a scalar).

In contrast, combining a vector with a scalar always results in a vector, and operations between two scalars always yield a scalar.

Sample:

Add vectors $C D$ and $D E$ , where $C D = (3, 4)$ and $D E = (2, 6)$

(spoiler)

$C D + D E = (3, 4) + (2, 6)$
$\Rightarrow C D + D E = (3 + 2, 4 + 6)$
$\Rightarrow C D + D E = (5, 10)$

Speed, velocity (average and instantaneous)

Speed is a scalar that measures how fast an object moves by quantifying the rate at which distance changes, without considering direction.

In contrast, velocity is a vector that not only indicates the rate of displacement but also specifies its direction.

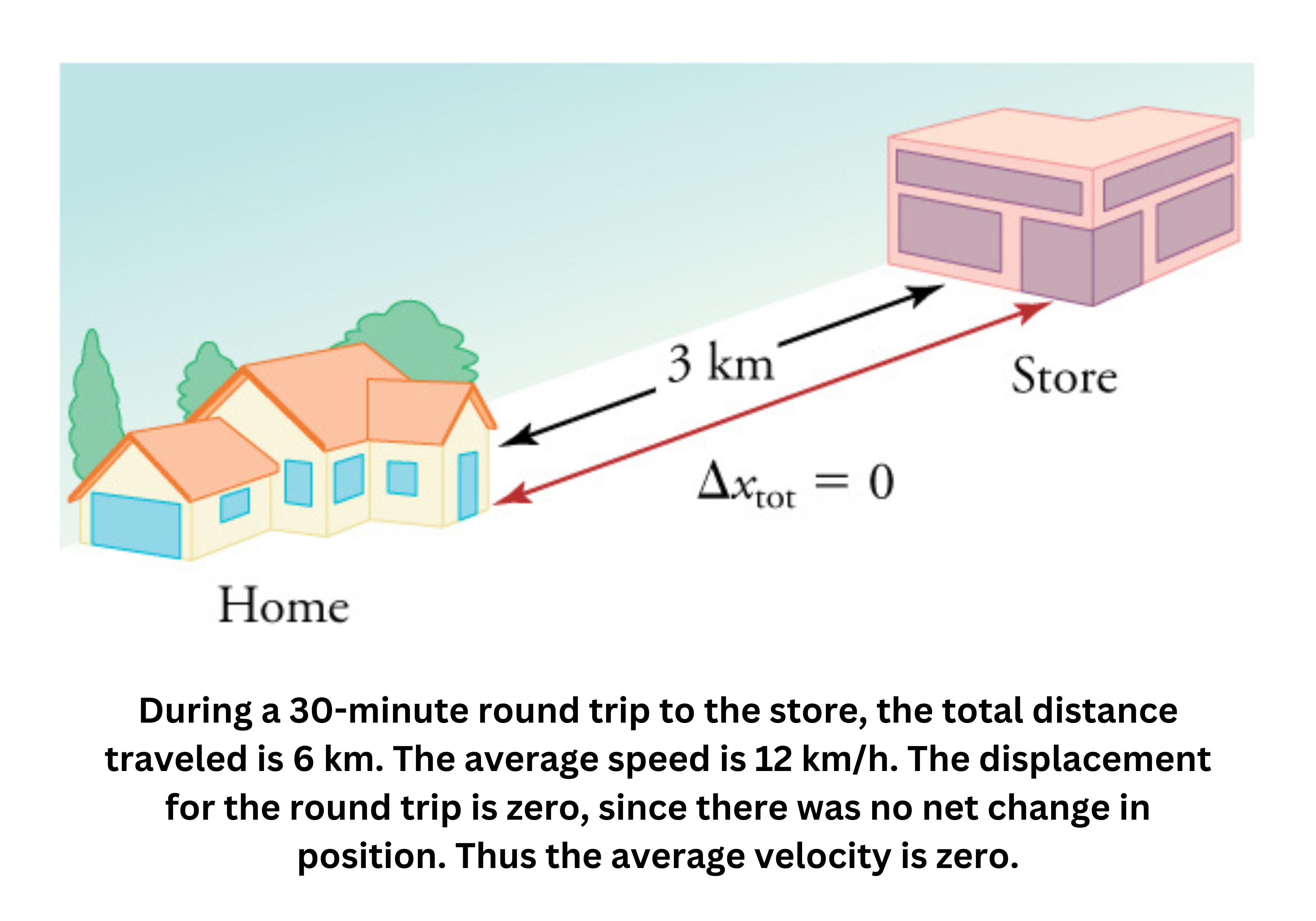
Average speed is computed by dividing the total distance traveled by the elapsed time, whereas average velocity is determined by dividing the net displacement by the time interval.

On a more precise scale, instantaneous speed refers to the speed measured at a specific moment over an infinitesimally small time period, and it equals the magnitude of instantaneous velocity. However, unlike instantaneous speed, instantaneous velocity includes direction—the direction of which is always tangent to the path at that exact point.

Average speed

$V = \frac{d}{t}$

$V_{a vg} = \frac{d}{t}$

Average velocity

$V = \frac{s}{t}$

$V_{a vg} = \frac{s}{t}$

Average acceleration

$a = \frac{Δ V}{Δ t}$

$a_{a vg} = \frac{V _{f} - V _{i}}{t}$

$($ $Δ V = V_{f} - V_{i}$ , i.e., final velocity minus initial velocity $)$

Acceleration

Average acceleration is defined as the rate at which velocity changes over time (final velocity - initial velocity).

In cases of uniformly accelerated motion along a straight line, where acceleration remains constant and there is no change in direction, certain simplifications arise. In this scenario, the numerical values for speed and velocity, as well as for distance and displacement, can be treated as equivalent—as long as the direction is kept in mind.

Under these conditions, the standard equations of uniform acceleration all apply:

$s = V_{a vg} \cdot t$

$V_{a vg} = \frac{V _{f} + V _{i}}{2}$

$V_{f}^{2} = V_{i}^{2} + 2 a s$

$s = \frac{1}{2} a t^{2} + V_{i} t$

$d_{f} = d_{i} + s or l_{f} = l_{i} + s$

$($ $d$ = distance or $l$ = length, take your pick $)$

Refresher about formulas, which you should both memorize and be able to manipulate:

Assign a consistent sign convention by designating one direction as positive and the opposite as negative, and then apply this uniformly in all calculations.

In Cartesian (graphing) coordinates, upward and rightward movements are typically positive, while downward and leftward are negative.

For free falls, however, it is common to define downward as positive (falling is what’s expected, so think of it as gain/progress).

Freely falling objects move under constant acceleration due to gravity, which on Earth is approximately $g$ = $9.8 m / s^{2}$ . Whether an object is dropped, thrown upward, or projected at an angle, it is considered to be in free fall. For ease of calculation, it’s common to assign downward as positive so that $g$ remains positive for objects dropped or thrown downward; when an object is tossed upward, its initial velocity has the opposite sign to $g$ .

In ideal conditions without air resistance, the net acceleration remains constant at $g$ because the force of gravity (weight) and the mass of the object are constant. When air resistance is present, the acceleration decreases over time as resistive forces build up, until eventually reaching terminal velocity, where the gravitational force is balanced by air resistance and acceleration ceases.

Projectiles are a specific case of free-falling bodies. Their vertical motion is always accelerated downward at $g$ , while their horizontal motion remains constant due to the absence of horizontal forces. To compute the time a projectile remains in the air, only the vertical component is considered; the horizontal distance traveled is then the product of this time and the constant horizontal velocity.

When an object is tossed straight upward and returns to its starting point, the overall displacement is zero because the upward and downward movements cancel each other out. In such cases, the time spent ascending equals the time spent descending.

Orbiting satellites are also in a state of free fall, continuously accelerating toward the Earth due to gravity. However, because they have sufficient tangential velocity, the Earth’s surface curves away at the same rate, preventing the satellite from colliding with the planet.

This consistent application of uniform acceleration in free fall underlies many calculations in physics, where the distinction between instantaneous and average values is crucial, and the direction of motion is accounted for through a chosen sign convention.

Displacement

Displacement in physics is a vector quantity that represents the change in an object’s position. It is defined by both its magnitude (the shortest distance between the starting point and the endpoint) and its direction. Unlike distance, which is a scalar that only measures the total length traveled, displacement focuses solely on the net change in position**, regardless of the path taken.

Average speed versus velocity during a round trip

Graphing position

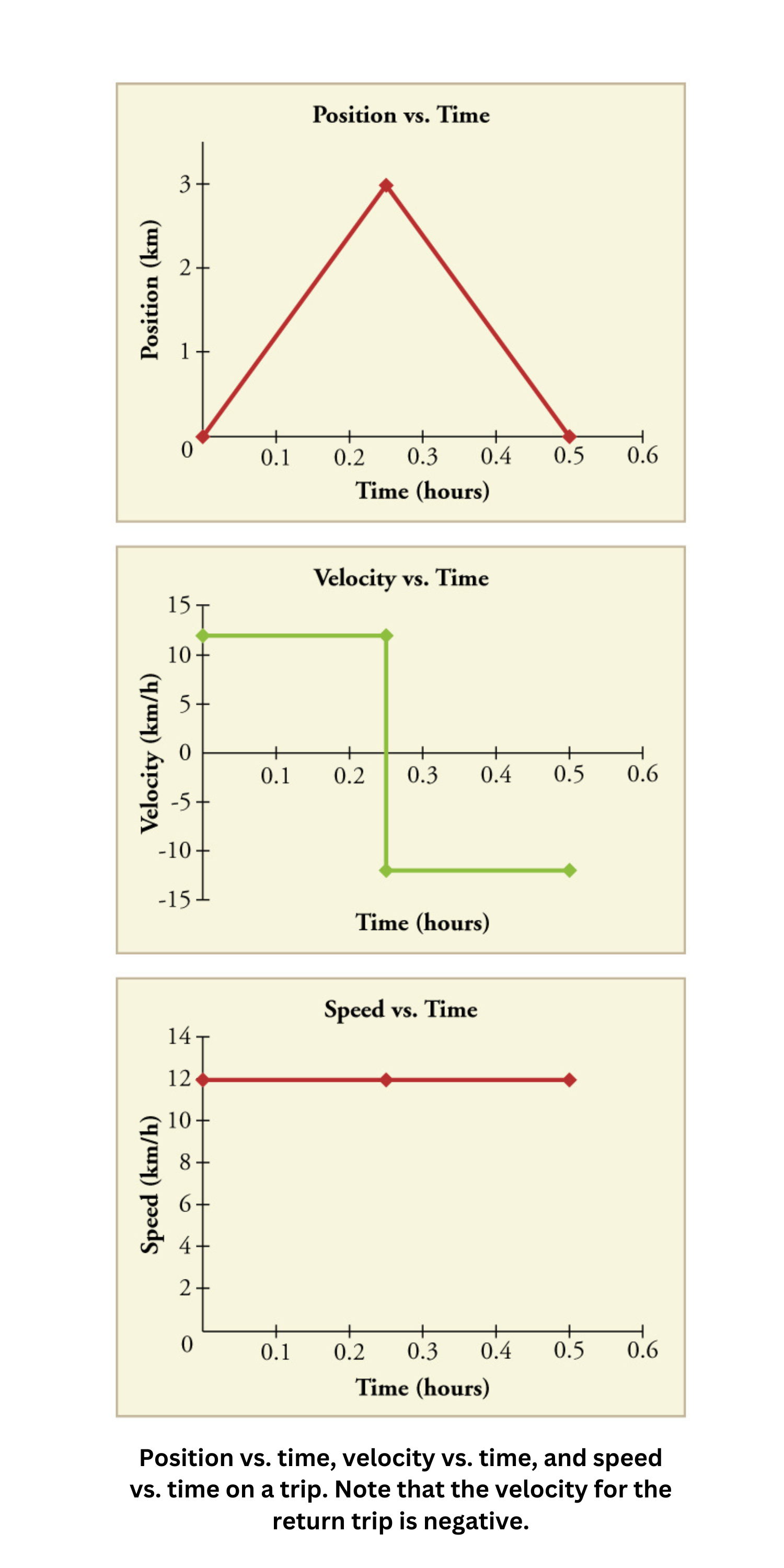
These simple models illustrate different ways that velocity, speed and position can be illustrated in terms of time. The more changes in speed or direction, the more complicated the plotting of the graphs will appear.

Position, velocity, and speed graphs on a trip