Fluids and circulatory system fluids

Fluids

Both liquids and gases are considered fluids because they can flow and conform to the shape of their containers.

A key property of fluids is density, which is defined as the mass ($m$) of an object divided by its volume ($V$), or:

$$\rho =\frac{m}{V}$$

For example, water typically has a density of 1 $\frac{\text{g}}{\text{mL}}$ (equivalent to 1 $\frac{\text{g}}{{\text{cm}}^3}$ or 1 $\frac{\text{kg}}{\text{L}}$).

Specific gravity is the ratio of the density of a substance to that of water, so water’s specific gravity is 1.

Buoyancy and Archimedes’ principle

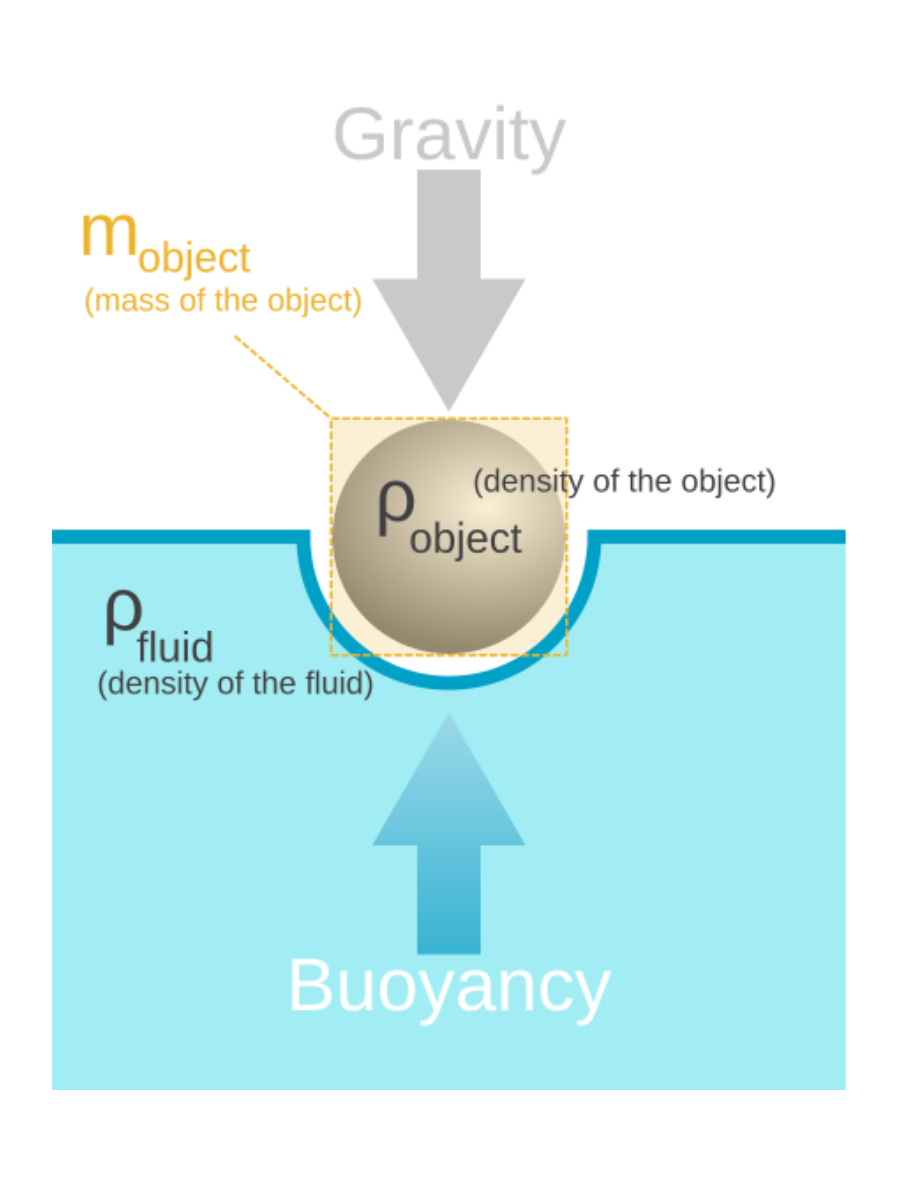
Buoyancy is explained by Archimedes’ principle, which states that the buoyant force on an object is equal to the weight of the fluid it displaces.

Mathematically, this is expressed as $F_B=m_{\text{displaced}}g={\rho }_{\text{fluid}}{V}_{\text{submerged}}g$ where $V_{\text{submerged}}$ is the volume of the object below the fluid surface.

Hydrostatic pressure

Hydrostatic pressure in fluids operates under Pascal’s law, which states that any pressure applied to a liquid is transmitted equally in all directions.

This concept is expressed by the equation, $F_1/A_1=F_2/A_2$ meaning that the pressure (force per unit area) at one point in the fluid is the same as at any other point.

Consequently, when a small force is applied over a small area, it can generate a much larger output force if applied to a larger area. Moreover, the relationship $A_1{d}_1=A_2{d}_2$ shows that the distance moved at each end adjusts so that the work done (force times distance) remains constant throughout the system.

In a fluid, pressure increases with depth according to

$$P=\rho gh$$

where $P$ is pressure, $\rho$ is the fluid density, $g$ is the gravitational constant, and $h$ is the depth below the surface.

At the surface, where $h=0$, the pressure contributed by the fluid is zero.

At any depth, the pressure is given by $\rho gh$, known as the gauge pressure because it does not include atmospheric pressure.

To obtain the absolute pressure on a submerged object, simply add the atmospheric pressure to $\rho gh$.

Viscosity: poiseuille flow and continuity equation ($A\cdot v$ = constant)

When a viscous fluid flows through a pipe, its flow front takes on a parabolic shape that bulges outward. This behavior is governed by the continuity equation, which states that the product of the cross-sectional area ($A$) and the linear velocity ($v$) remains constant ($A\cdot v$ = constant). In other words, the volume flow rate ($dV/dt$) is constant throughout the pipe. Since $dV$ can be expressed as the product of the area and a small length ($dL$) along the pipe ($dV=A\cdot dL$), it follows that $A\cdot (dL/dt)$ equals $A\cdot v$, reinforcing that the flow rate does not change along the pipe.

Concept of turbulence at high velocities

At low speeds, fluid exhibits laminar flow, where the movement is smooth and orderly.

When the velocity increases, the fluid transitions into turbulent flow, marked by chaotic motion and the formation of swirling eddies.

Surface tension enables the liquid’s surface to support very light objects—such as insects walking on water—due to the cohesive forces between molecules of the solvent.

Venturi effect, pitot tube

The Venturi effect describes how a fluid’s pressure decreases when it flows through a constricted section of a pipe or channel. According to Bernoulli’s principle, as fluid velocity increases in a narrower passage, the kinetic energy per unit volume rises, so the pressure must drop. Engineers use this effect in devices like Venturi meters to measure flow rates by comparing pressures at the wider and narrower parts of a tube.

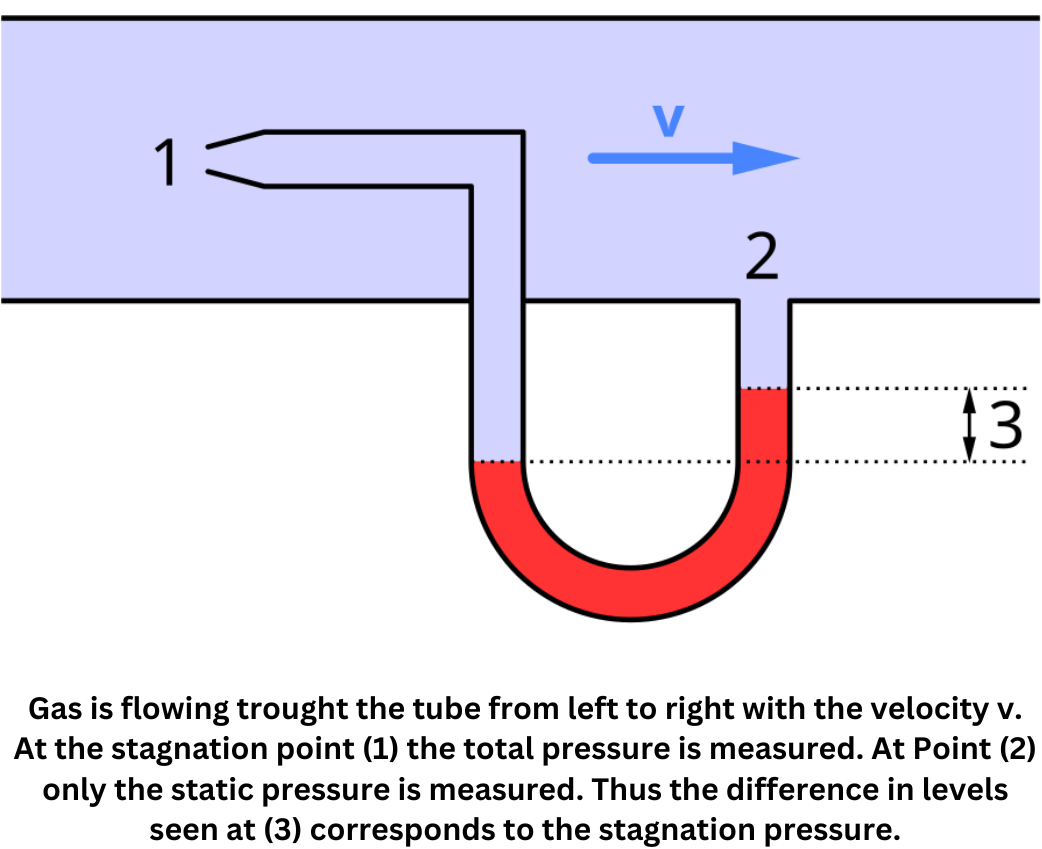
A pitot tube is a device designed to measure the speed of a moving fluid—commonly air around an aircraft. It features an opening aligned with the flow, capturing stagnation pressure, which combines the fluid’s static pressure and the dynamic pressure from its motion. By comparing this stagnation pressure to the static pressure measured elsewhere, the pitot tube helps determine the fluid’s velocity, applying Bernoulli’s principle to relate pressure differences to flow speed.

Circulatory system physics arterial and venous systems; pressure and flow characteristics

In the arterial system, the heart provides a high‐pressure pulse that propels blood through relatively narrow vessels with strong, elastic walls. This design maintains arterial pressure and modulates blood flow, ensuring that each heartbeat delivers a surge of blood at sufficient velocity. According to the continuity equation, fluid velocity is inversely related to cross‐sectional area, so the arteries—though narrower than veins—carry blood under higher pressure and moderate flow speed.

As blood transitions into smaller arterioles and capillaries, the combined cross‐sectional area expands greatly, causing flow velocity to slow. This slowdown facilitates nutrient exchange and gas exchange between blood and tissues. By the time blood enters the venous system, the pressure drops considerably. The veins feature thinner, more compliant walls that can stretch to accommodate varying blood volume, contributing to a lower venous pressure overall.

Because venous blood returns under low pressure, several mechanisms support venous return:.

• Skeletal muscle contractions compress veins, pushing blood forward, while valves in the veins prevent backflow—together forming a “muscle pump.”
• Additionally, variations in thoracic pressure during respiration help draw blood toward the heart, reinforcing venous flow against the pull of gravity.

This coordination between the arterial and venous systems manages fluid pressure and flow, ensuring a closed‐loop circulatory system capable of adapting to changing demands.