Gas phase

Absolute temperature, ( $K$ ) Kelvin scale

The absolute temperature scale, measured in Kelvin $(K)$ , places its zero point at absolute zero, the lowest possible temperature where no further heat energy can be extracted from a substance. This scale aligns directly with the Celsius $(° C)$ scale by using the relation $K = ° C + 273$ . As a result, water freezes at $273 K$ ( $0° C$ ) and boils at $373 K$ $(100° C)$ .

Though the Fahrenheit ( $° F$ ) scale remains widely used in some regions (where $° F = 1.8 \times ° C + 32$ ), the Kelvin scale is fundamental in scientific contexts because it begins at the theoretical point of zero thermal energy.

Description	Celsius ( $C^{\circ}$ )	Kelvin ( $K$ )	Fahrenheit ( $F$ )
Surface of the sun	5600	5900	10100
Boiling point - water	100	373	212
Body temperature	37	310.2	98.6
Room temperature	20	293	68
Cool day	10	283	50
Freezing point - water	0	273	32

Pressure, simple mercury barometer

Pressure is defined as the force exerted per unit area, expressed by the equation

$P = \frac{F}{A}$

where $F$ represents the applied force and $A$ is the area over which this force acts.

At sea level, the atmospheric pressure is about $101 k P a$ , equivalent to $1 a t m$ , and it decreases with increasing elevation.
A mercury barometer measures this pressure by allowing the atmosphere to push a column of mercury upward; one end of the barometer is open to the air while the other is sealed to form a vacuum.

The pressure is determined by the weight of the mercury that is lifted ( $F$ ) divided by the cross-sectional area ( $A$ ) of the tube.
Standard barometers are calibrated so that 1 atm of pressure raises the mercury to $760 mm$ , also referred to as $760 mm H g$ or $760 T orr$ .
When performing calculations using the formula, ensure that force is in Newtons ( $N$ ) and area is in square meters ( $m^{2}$ ), which results in pressure measured in Pascals ( $P a$ ).

Molar volume

Molar volume at 0 degrees Celsius and $1 a t m$ is 22.4 $L / m o l$ . This means that ideal gases occupy 22.4 liters per mole of molecules. Remember, it’s 22.4 liters per mole, not the reverse. =

A mole consists of approximately $6.02 \times 1 0^{23}$ particles, which is an enormous number of molecules that take up a considerable volume. For instance, consider that air is mostly composed of nitrogen; in its diatomic form ( $N_{2}$ ), nitrogen has a molar mass of about 28 grams. Because air is very light, a full mole of it occupies 22.4 liters at standard conditions.

Ideal gas

An ideal gas is defined by the kinetic molecular theory, which models the gas as a collection of point particles that move randomly and collide elastically with each other and the container walls.

In an ideal gas, the molecular volume is negligible and there are no intermolecular forces. This ideal behavior is observed under conditions of low pressure and high temperature, where molecules are sufficiently separated; however, at high pressures and low temperatures, the proximity of molecules leads to significant intermolecular interactions and volume effects, eventually causing the gas to condense.

The behavior of an ideal gas is described by the ideal gas law:

$P V = n R$

where $P$ represents pressure, $V$ is volume, $n$ is the number of moles, $R$ is the gas constant, and $T$ is temperature

This law underlies the combined gas law, which shows that when $n$ and $R$ are constant, the ratio $\frac{P V}{T}$ remains constant. From this relationship, Boyle’s law ( $P_{1} V_{1} = P_{2} V_{2}$ at constant $T$ ) and Charles’s law ( $V \propto T$ at constant $P$ ) can be derived, as well as Avogadro’s law, which states that equal volumes of gas at the same temperature and pressure contain equal numbers of moles.

Kinetic molecular theory of gases

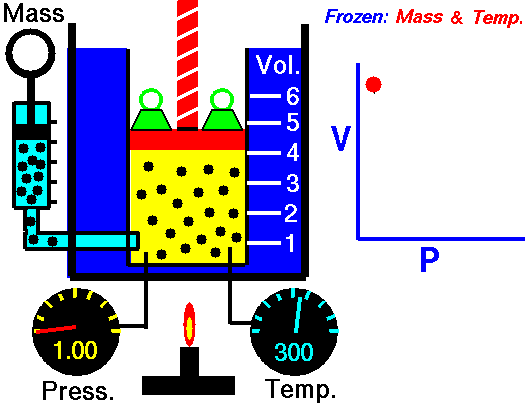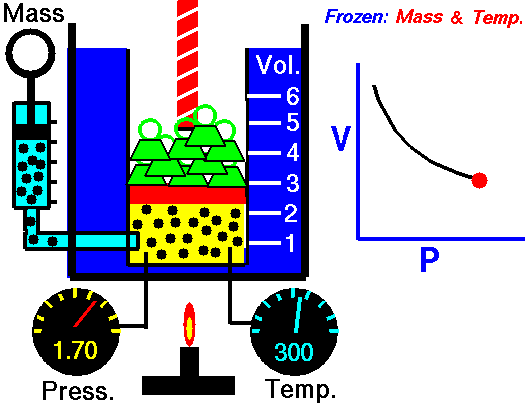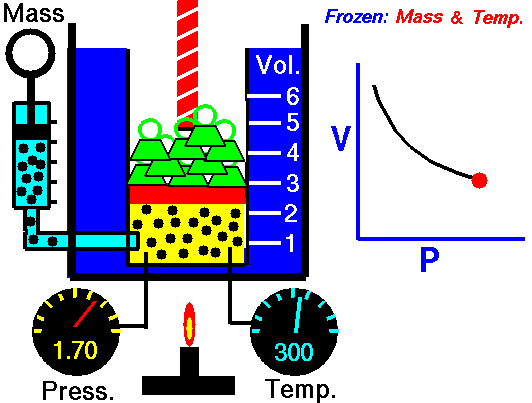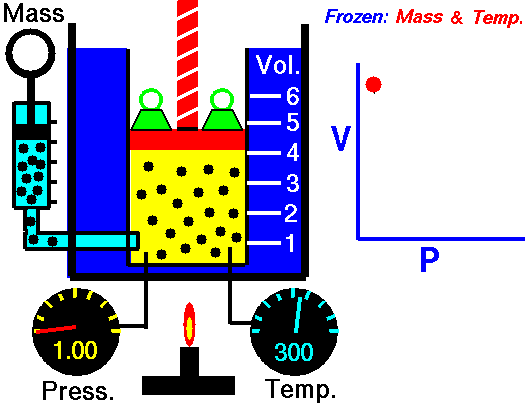
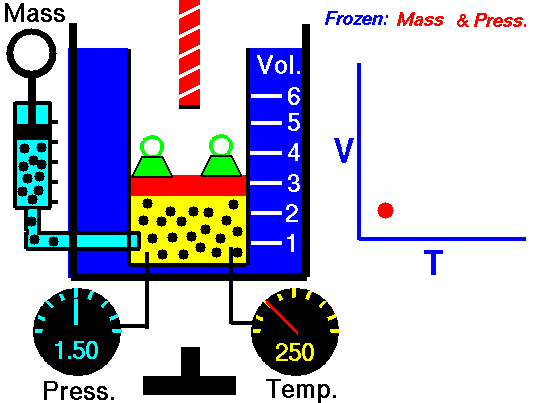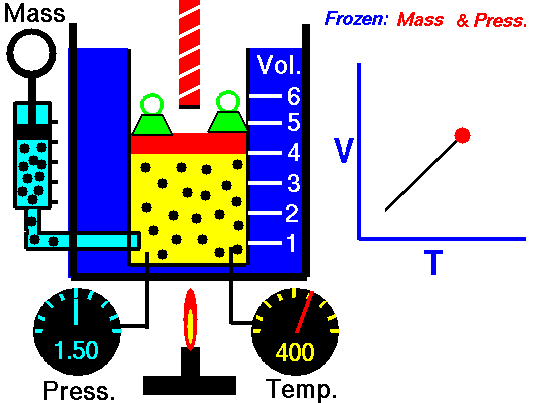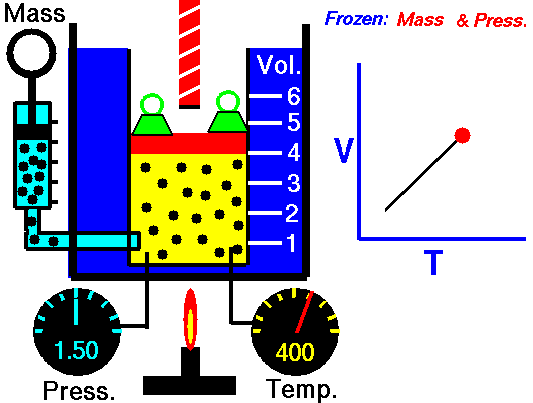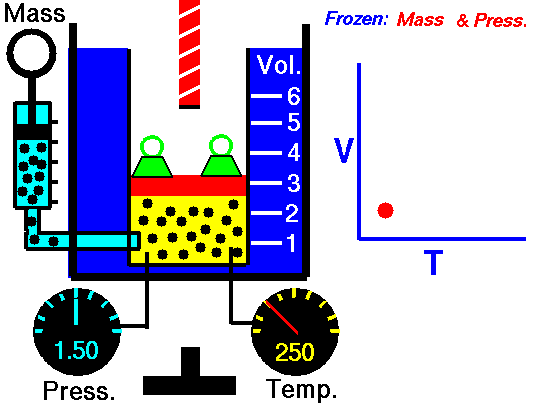
The kinetic molecular theory explains the behavior of gases and underpins the ideal gas laws. It assumes that gas molecules are in constant, random molecular motion, experience no intermolecular forces, and have negligible molecular volume. Additionally, all collisions are perfectly elastic collisions, ensuring that the total kinetic energy remains constant during interactions.

In this model, pressure arises from the molecules colliding with the container walls, and because these collisions occur randomly, the pressure is evenly distributed throughout the container. Temperature is a measure of the average kinetic energy of the gas molecules, so

higher temperatures correspond to faster molecular speeds
lower temperatures indicate slower motion.

Heat capacity at constant volume and at constant pressure

The heat capacity at constant volume is the amount of heat required to raise a system’s temperature by one degree while keeping its volume fixed, so that no work is done by expansion.

In contrast, the heat capacity at constant pressure is the heat needed to increase the temperature by one degree while the pressure remains constant; in this case, some energy is used for expansion work, making it higher than the constant-volume heat capacity. The difference between these two is accounted for by the work done against the surroundings.

Boltzmann’s constant is a fundamental value that connects the average kinetic energy of individual particles with the macroscopic temperature of a system, serving as a bridge between microscopic behavior and bulk thermal properties.

Diffusion and effusion, graham’s law

Diffusion is the process in which molecules move randomly from regions of higher concentration to lower concentration, effectively traveling down their concentration gradient.
In contrast, effusion occurs when gas molecules escape through a very small opening in a container, again driven by their random motion.

Both diffusion and effusion are described by Graham’s law, which states that the rate of diffusion or effusion of a gas is inversely proportional to the square root of its molecular weight ( $R a t e_{1} / R a t e_{2} = (M_{2} / M_{1})$ .

This means that at a given temperature—where all gases have the same average kinetic energy—a lighter gas (with a lower molecular weight) will diffuse or effuse more rapidly than a heavier one. For example, if two different gases are introduced at opposite ends of a tube, the lighter gas will travel faster, causing the gases to meet at a point closer to the heavier gas’s end.

This law is rooted in the kinetic theory, which establishes that the average kinetic energy ( $½ m v^{2}$ ) is the same for all gases at the same temperature, leading to the relationship $v_{1} / v_{2} = (M_{2} / M_{1})$ for their velocities

Deviation of real gas behavior from the Ideal Gas Law, Van der Waals

In an ideal gas, molecules are assumed to have negligible volume and no interactions, a good approximation at low pressure and high temperature when they are far apart.

However, at higher pressures or lower temperatures, molecules are closer together and begin to experience intermolecular attractions, which pull them toward each other and effectively reduce the pressure. When they are forced into extremely close proximity, their finite sizes result in steric repulsion, which pushes them apart and increases the pressure.

These deviations from ideal behavior are quantitatively described by the Van der Waals equation, which introduces two constants: $a$ accounts for attractive forces (lowering the pressure) and $b$ represents the finite molecular volume (raising the pressure).

Partial pressure, mole fraction, and Dalton’s Law

Partial pressure is the pressure exerted by an individual gas within a mixture, and the total pressure is the sum of all these partial pressures.

The proportion of a specific gas in the mixture is given by its mole fraction, defined as the number of moles of that gas divided by the total number of moles in the mixture.

Dalton’s law states that the partial pressure of any gas is equal to its mole fraction multiplied by the total pressure, expressed as $P_{i} = χ_{i} \cdot Pt o t a l$ . This relationship means that $Pt o t a l = Σ$ $P_{i}$ = $Σ$ $χ_{i} \cdot Pt o t a l$ , linking the composition of the gas mixture directly to its pressure.

Partial pressures of main atmospheric gases at sea level

Absolute temperature, (K) Kelvin scale