Circuit elements, conductivity, and magnetism

Circuit elements

The current in a circuit represents the rate of charge flow through the cross-section of a conductor, defined by the equation $I = Δ Q /Δ t$ . Conventionally, current is taken to flow in the direction that positive charges would move, even though in many cases the actual charge carriers are electrons. The standard unit for current is Coulombs per second $(C / s)$ , which is also known as the Ampere.

Electromotive force, voltage

Electromotive force (emf) is not an actual force but a measure of the potential difference provided by a source, expressed in volts. A battery serves as a common source of emf. In an ideal battery with no internal resistance, the potential difference across its terminals exactly equals its emf. However, when a battery has internal resistance, some of the emf is lost as a voltage drop within the battery, so the measured terminal voltage is reduced by that amount.

The terminal potential is the measurable voltage across a battery’s external terminals when it is connected to a circuit. A battery is not a perfect voltage source; it contains an inherent internal resistance that acts like a small resistor connected in series with an ideal voltage source. Because of this internal resistance, some of the energy provided by the battery’s EMF (electromotive force) is lost as a voltage drop when current flows. Consequently, the terminal potential is given by the equation:

Terminal potential $= EMF - I \cdot R_{in t er na l}$ , where $I$ is the current.

This explains why, under load, the voltage available to external devices is lower than the battery’s nominal EMF.

Resistance

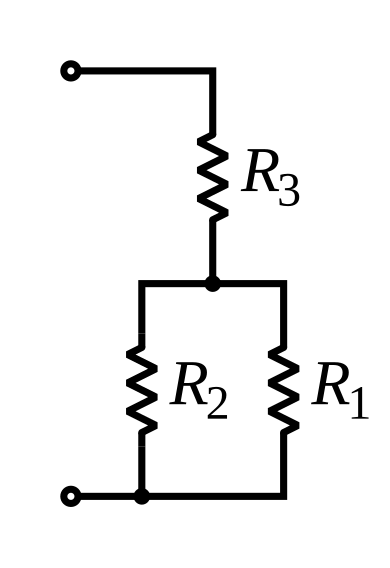
Ohm’s law states that current $(I)$ is the ratio of voltage $(V)$ to resistance $(R)$ , expressed as $I = V / R$ . In circuit design, resistors can be configured in series or parallel.

For resistors in series, the same current flows through each component, and the total voltage is the sum of the individual voltage drops, with each drop determined by $V = I \cdot R$ or ( $I = V / R$ ).

In contrast, for resistors in parallel, the voltage across each resistor is identical while the total current is the sum of the currents through each branch; here, a resistor with a higher resistance carries a lower current.

The material property known as resistivity $(ρ)$ relates to resistance through the equation $R = ρ L / A$ , where $L$ is the length and $A$ is the cross-sectional area of the conductor. Lower resistivity, shorter length, and larger area all reduce resistance, which is why devices like extension cords are constructed with thick wires to minimize heating and energy loss.

Resistors in series and parallel combinations

Capacitance

A capacitor stores electrical energy by accumulating charge on two conductive plates separated by an insulating gap. In a parallel-plate capacitor, the capacitance is defined by the equation

$C = Q / V = ϵ A / d$

where $Q$ represents the stored charge, $V$ is the voltage across the plates, $A$ is the plate area, $d$ is the distance between them, and $ε$ is the permittivity of the medium. The voltage can also be described by $V = E d$ , with $E$ being the electric field between the plates.

The energy stored in a charged capacitor is given by

$U = \frac{1}{2} Q Δ V = \frac{1}{2} C (Δ V)^{2} = \frac{Q ^{2}}{2 C}$

where U is the potential energy.

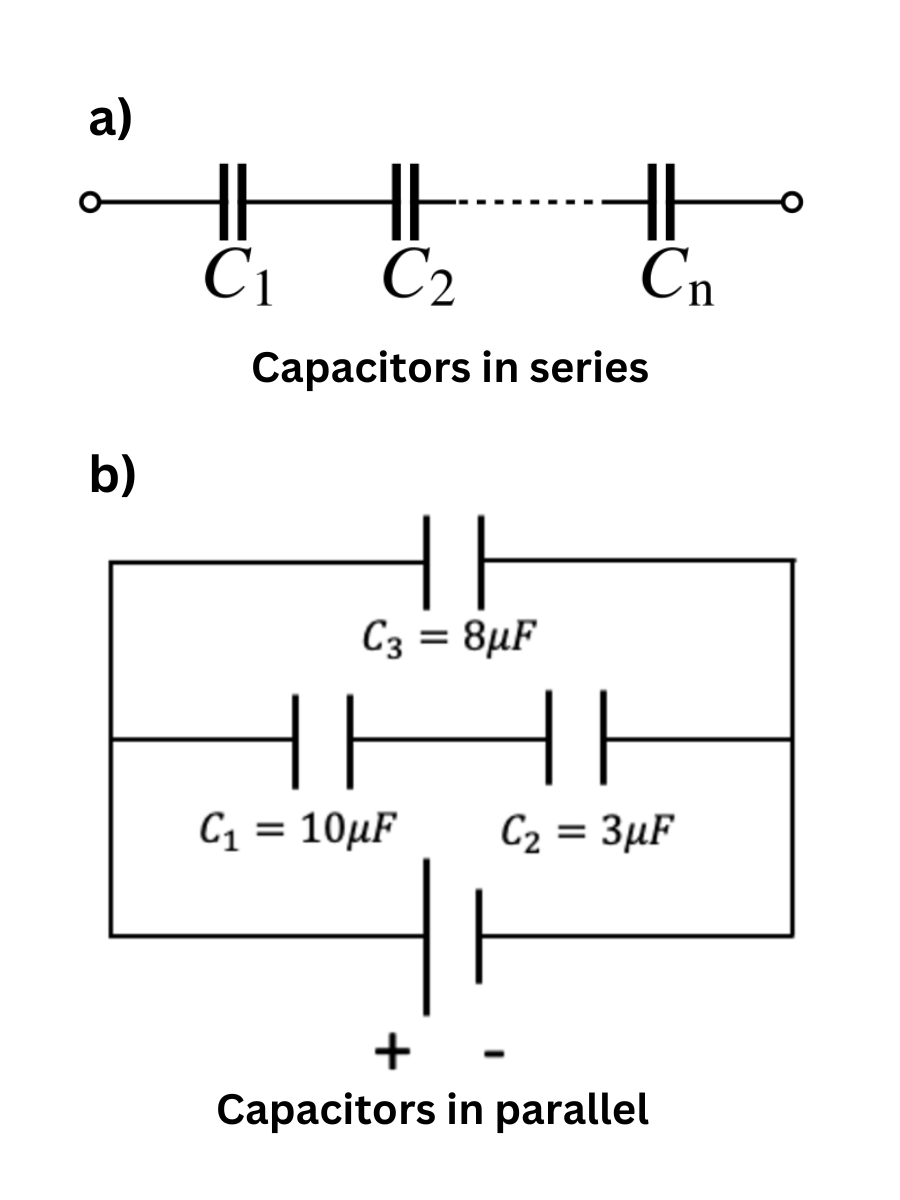
Capacitors can be connected in series, where the reciprocal of the equivalent capacitance is the sum of the reciprocals of the individual capacitances, or in parallel, where the equivalent capacitance is the sum of the individual capacitances.

Introducing a dielectric (a nonconducting material) between the plates increases the capacitance by either allowing more charge to be stored for a given voltage or reducing the voltage for a fixed charge. With a dielectric, the voltage becomes $V = V_{0} / κ$ and the capacitance becomes $C = κ C_{0}$ , where $κ$ is the dielectric constant.

Discharge of a capacitor

During the discharge process, a capacitor releases its stored charge by driving a current through an external resistor. In effect, the capacitor functions like a battery, supplying energy to the circuit until its charge is depleted. As the capacitor discharges, the current decreases over time, reflecting the gradual loss of stored energy.

Conductivity

Conductivity is a measure of how easily a material can carry an electrical current. In solutions, the electrolyte concentration is crucial: without electrolytes, no ionization occurs, and thus no conductivity exists; at an optimal concentration, ions move most freely, maximizing conductivity; however, when the concentration is too high, ions crowd together, reducing their mobility and lowering conductivity.

Temperature also plays a significant role. In metals, increased temperature leads to a decrease in conductivity due to enhanced lattice vibrations that scatter electrons.

In semiconductors, however, higher temperatures typically increase conductivity by generating more charge carriers.

At extremely low temperatures, some materials exhibit superconductivity, where electrical current flows without any resistance.

Conductivity $(σ)$ is mathematically defined as the inverse of resistivity $(ρ)$ . For practical applications, one can measure conductivity by placing a capacitor in a solution; the current that flows between the capacitor’s plates reflects the solution’s ability to conduct electricity.

Meters

An ammeter is an instrument designed to measure the current flowing through a circuit.

An ohmmeter is a device used to determine the resistance of a component.

A probe is a part of a measuring instrument that connects the meter to the circuit or component under investigation.

A voltmeter measures the voltage, or electrical potential difference, between two points in a circuit.

Magnetism

Definition of magnetic field $B$

The magnetic field $(B)$ is a vector field present in regions where a moving charge experiences a force due to its motion. In essence, when a charged particle moves through a space containing a magnetic field, it is deflected by a force whose magnitude and direction depend on both the particle’s velocity and the field’s strength. This force can be measured in Teslas $(T)$ , which are also expressed in units of $N \cdot s / m \cdot C$ .

Motion of charged particles in magnetic fields; Lorentz force

When a charged particle moves through a magnetic field, it experiences an electromagnetic force given by

$F = q v B sin θ$

where $q$ is the charge, $v$ is the velocity, $B$ is the magnetic field, and $θ$ is the angle between the velocity and the magnetic field.

This force is always perpendicular to both the direction of motion and the magnetic field. You can use the right hand rule to determine its direction: point your thumb in the direction of the positive charge’s velocity, your middle finger in the direction of the magnetic field, and your palm will face in the direction of the force.

In cases where a charge moves in a circular path, the electromagnetic force acts as the centripetal force needed to keep the particle in orbit, satisfying $F = m v^{2} / r$ . For current-carrying wires, the force can be expressed as $F = i L B sin θ$ , where $i$ is the current and $L$ is the length of the wire. Here, the current is treated as the motion of positive charges, and applying the same right hand rule shows that wires with currents in the same direction attract each other, while those with currents in opposite directions repel.