Types of variables: Qualitative or categorical variables are included in nominal and ordinal scales. Quantitative or continuous variables are included in interval or ratio scales.
Nominal scale: Values are categories without any numerical ranking, such as county of residence, vaccinated or unvaccinated, male or female etc. Yes/No scale is also nominal.
Ordinal scale: Values that can be ranked but are not necessarily evenly spaced, such as stages of cancer. Values are arranged in groups or classes in an ascending or descending order e.g. Stage I breast cancer is less severe than Stage IV.
Interval scale: Values can be measured on a scale of equally spaced units, but without a true zero point, such as date of birth.
Ratio scale: It includes interval variables with a true zero point, such as height in centimeters or duration of illness.
Categorical variables are usually further summarized as ratios, proportions, and rates. Continuous variables are often further summarized with measures of central location and measures of spread.
Frequency distribution:
Normal or symmetric or Gaussian distribution: In such a frequency distribution, the data seem to cluster around a central value. It forms the classic bell-shaped curve when plotted on a graph. The clustering at a particular value is known as the central location or central tendency of a frequency distribution. The mean, median and mode are the same in a normal distribution.
Bell curve
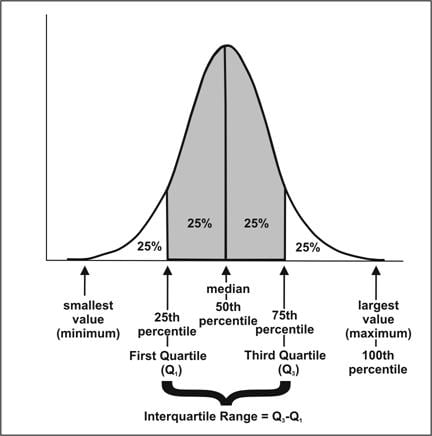
Bell-shaped curve. The central tendency, the middle is the median, 50th percentile. 25% to the left is the 25th percentile, the first quartile (Q1). 25% to the right of the median is the 75th percentile, the third quartile (Q3). The interquartile range goes from Q1 to Q3 and makes up 50% of the area under the curve. The largest value is the 100th percentile.
Three bell curves
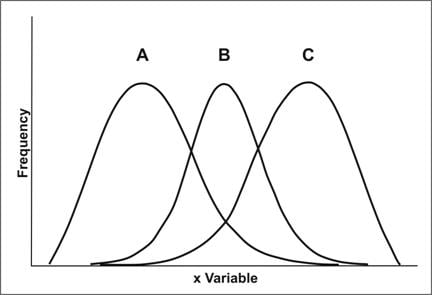
Three superimposed bell curves. The shapes of all three are different. A is shifted to the left. B is symmetrical. C is shifted to the right.
Measures of central location
Arithmetic mean: Simply the average of all data. The arithmetic mean is the best descriptive measure for data that are normally distributed. It is not useful in skewed data as the mean can be affected by extreme values.
Median: It is the middle value of a set of data that has been put into rank order. The median is also the 50th percentile of the distribution.
Mode: It is the value that occurs most often in a set of data
Geometric mean: It is the mean or average of a set of data measured on a logarithmic scale. The geometric mean is used when the logarithms of the observations are distributed normally (symmetrically) rather than the observations themselves. It is useful in microbiological assays.
Problem 1: Calculate the mode from the following data set
1, 1, 2, 2, 2, 3, 3, 3, 3, 3,
(spoiler)
Answer is 3 (most common value).
Problem 2: Calculate the median from the following data set
4, 23, 28, 31, 32
(spoiler)
Answer is 28 (as it is the middle value).
Problem 3: Calculate the median from the following data set
4, 23, 28, 30, 31, 32
(spoiler)
As the data set has an even number of values, take an average of the middle two values
In the above example, it will be 28+30/2 = 58/2 = 29.
Problem 4: Calculate the arithmetic mean from the following data set
1, 1, 2, 2, 2, 3, 3
(spoiler)
To calculate add all the values and divide by the number of values.
In the above example it will be 1+1+2+2+2+3+3 = 14 /7 = 2
Asymmetric or skewed distribution: In skewed distributions, the data are distributed in an asymmetric fashion. Skewness refers to the tail, not the hump. So a distribution that is skewed to the left has a long left tail. A distribution that has a central location to the left and a tail off to the right is said to be positively skewed or skewed to the right. A distribution that has a central location to the right and a tail to the left is said to be negatively skewed or skewed to the left.
In right skewed distributions, Mode < Median < Mean
In left skewed distributions, Mean < Median < Mode
Sign up for free to take 1 quiz question on this topic
