Acid/base equilibria

Acid/base equilibrium involves a reversible reaction between a Bronsted acid, which donates a proton, and a Bronsted base, which accepts a proton. In this process, the acid forms its conjugate base after losing a proton, while the base becomes its conjugate acid upon gaining a proton.

Ionization of water

A classic example is the ionization of water, represented by $H_{2}O\leftrightarrow H^{+}O{H}^{-}$ .

The product of the hydrogen ion concentration ([$H^{+}$]) and the hydroxide ion concentration ([$O{H}^{-}$]) is given by the $K_w$, which is approximately $1\times 10^{-14}$ at $25°$C.

The pH of a solution is defined as the negative logarithm of $[H^{+}]$ ($pH=-log[H^{+}]$) ; for pure water, with $[H^{+}]$ = $10^{-7}\text{M}$, the pH is $7$, indicating a neutral solution.

A solution is acidic if its pH is less than $7$ and basic if its pH is greater than $7$. Additionally, the $pOH$ is defined as –$log[O{H}^{-}]$ and, at $25°$C, $\text{pH}$ + $\text{pOH}=14$.

Conjugate acids and bases (e.g., $N{H}_4^{+}$ and $N{H}_3$)

Acid/base equilibria involve the interplay between acids, bases, and their corresponding conjugate acids and conjugate bases. When an acid donates a proton, it forms its conjugate base; similarly, when a base accepts a proton, it becomes its conjugate acid.

—Insert Image 173—

• In strong acids and strong bases, complete dissociation occurs because their conjugate species are highly stable.
• Weak acids and weak bases only partially dissociate due to the moderate stability of their conjugate species.
• This equilibrium can be shifted by the presence of a common ion, as explained by Le Chatelier’s principle; for instance, acetic acid ($C{H}_{3}OOH$) dissociates less in the presence of its salt, $C{H}_{3}COONa$, and ammonium hydroxide ($N{H}_{4}OH$) shows reduced dissociation when $N{H}_{4}Cl$ is added.

Calculation of pH of solutions of salts of weak acids or bases

Consider a 0.10 M aqueous solution of sodium acetate ($C{H}_{3}COONa$). In water, sodium acetate dissociates completely into $N{a}^{+}$ and $C{H}_{3}CO{O}^{-}$ (acetate ion). The relevant equilibrium is the hydrolysis of the acetate ion:

$${\text{CH}}_3{\text{COO}}^{-}+H_{2}O\rightleftharpoons {\text{CH}}_3\text{COOH}+O{H}^{-}$$

Acid/base constants:

Acetic acid ($C{H}_{3}COOH$) has a dissociation constant of $Ka=1.8\times 10^{-5}$. Since $C{H}_{3}CO{O}^{-}$ is the conjugate base of a weak acid, we use:

$$K_b=\frac{K_w}{K_a}=\frac{1.0\times 10^{-14}}{1.8\times 10^{-5}}\approx 5.6\times 10^{-10}.$$

Setting up the equilibrium expression:

Let $x$ represent the concentration of $O{H}^{-}$ produced by acetate hydrolysis. The equilibrium expression for the reaction is:

$$K_b=\frac{[{\text{CH}}_3\text{COOH}][O{H}^{-}]}{[{\text{CH}}_3{\text{COO}}^{-}]}.$$

Initially,

$$[{\text{CH}}_3{\text{COO}}^{-}]=0.10\text{M},[O{H}^{-}]=0.$$

At equilibrium,

$$[{\text{CH}}_3\text{COOH}]\approx x,[O{H}^{-}]=x,\text{and}[{\text{CH}}_3{\text{COO}}^{-}]\approx 0.10-x.$$

Since $x$ is very small, we approximate:

$$[{\text{CH}}_3{\text{COO}}^{-}]\approx 0.10\text{M}.$$

Thus, the equilibrium expression becomes:

$$5.6\times 10^{-10}=\frac{x^2}{0.10}.$$

Solving for $x$:

$$x^2=(5.6\times 10^{-10})\times 0.10=5.6\times 10^{-11},$$

$$x=\sqrt{5.6\times 10^{-11}}\approx 7.5\times 10^{-6}.$$

Therefore,

$$[O{H}^{-}]=7.5\times 10^{-6}\text{M}.$$

Calculating pOH and pH:

$$\text{pOH}=-\log [O{H}^{-}]=-\log (7.5\times 10^{-6})\approx 5.12,$$

$$\text{pH}=14-\text{pOH}=14-5.12=\mathrm{8.88.}$$

Hence, a $0.10M$ solution of sodium acetate is basic, with a $pH\approx 8.88$. This occurs because the acetate anion (the weak base) partially hydrolyzes, generating $O{H}^{-}$ and raising the $pH$ above $7$.

Equilibrium Constants $K_a$ and $K_b$: $p{K}_a$, $p{K}_b$

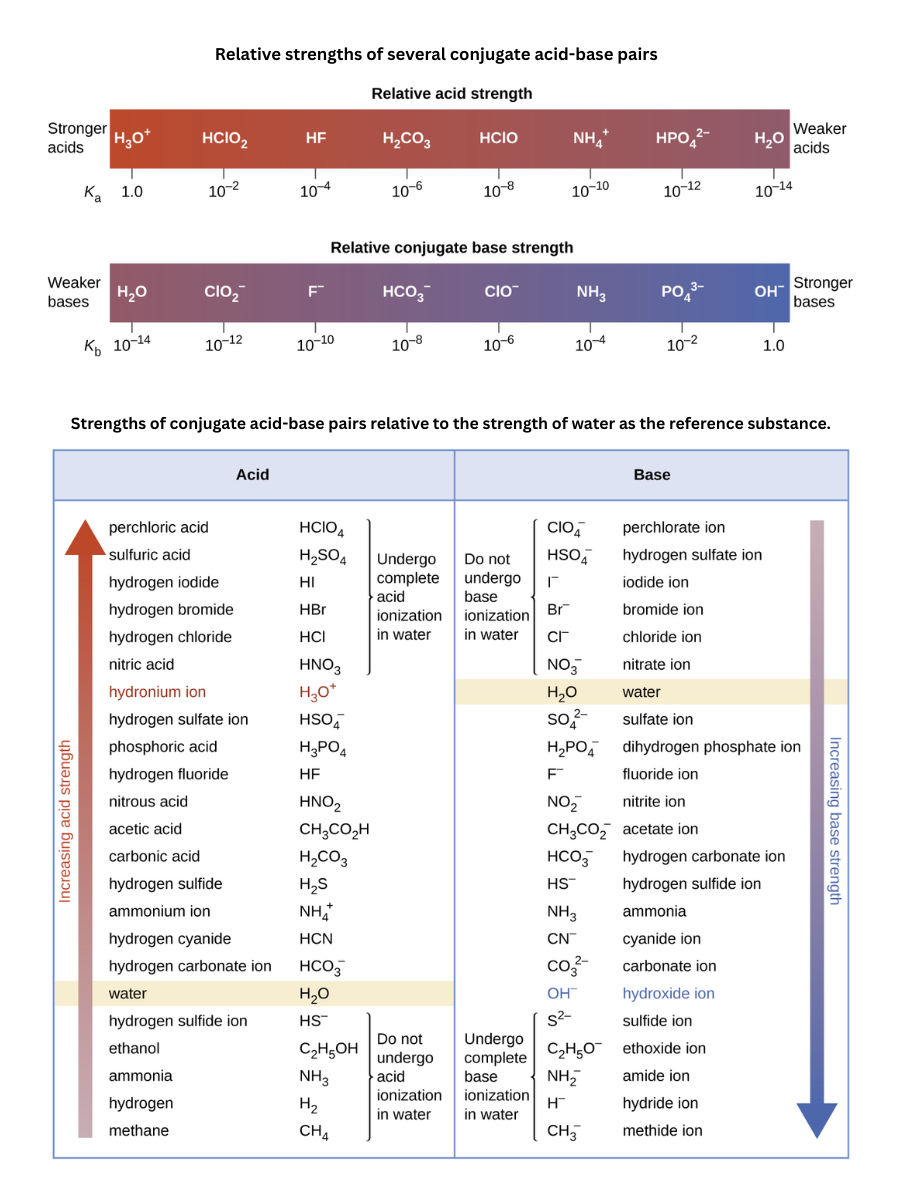
The acid dissociation constant ($K_a$) quantifies the extent to which an acid releases protons ($H^{+}$), as described by the equilibrium:

$$\text{H-Acid}\leftrightarrow H^{+}+{\text{Acid}}^{-}$$

In parallel, the base dissociation constant ($K_b$) measures how strongly a base accepts protons from water, following the equilibrium:

$$\text{Base}+H_{2}O\leftrightarrow {\text{H-Base}}^{+}+O{H}^{-}$$

Note that water is not included in these expressions because its concentration remains constant.
For a conjugate acid-base pair, the product of Ka and Kb equals the ionization constant of water ($K_w$), typically 10⁻¹⁴. To facilitate comparison, the pKa and pKb values are defined as the negative logarithms of Ka and Kb, respectively

$$\text{pKa}=-\log K_a\text{and}\text{pKb}=-\log K_b$$

and for any conjugate pair,

$$\text{pKa}+\text{pKb}=14$$

Buffers

Buffers are solutions that resist changes in pH by maintaining an equilibrium between an acidic species and its conjugate base. In these systems, the acidic component donates protons when the pH rises, while the basic component accepts protons when the pH falls, thus stabilizing the solution.

Buffers are typically composed of salts derived from weak acids and weak bases. Maximum buffering capacity occurs when the concentrations of the acid and its conjugate base are equal, which corresponds to a pH equal to the $p{K}_a$ of the acid, or, for a weak base, pH equal to 14 minus the $p{K}_b$.

Influence on titration curves

On a titration curve, the buffering region is seen as a relatively flat segment near the point of inflection, typically spanning about one pH unit above and below the $p{K}_a$ (or 14 - $p{K}_b$).