Rate processes in chemical reactions - Kinetics and equilibrium | Principles of chemical thermodynamics and kinetics, enzymes | Chem/phys

Reaction rate

A reaction rate measures how quickly reactants are consumed or products form, typically expressed in molarity per second (M/s). Mathematically, it can be written as:

$Rate = - \frac{Δ [ Reactant ]}{Δ t} or \frac{Δ [ Product ]}{Δ t}$

Dependence of reaction rate on concentration of reactants

The rate law links the reaction rate to the concentrations of reactants raised to specific exponents:

$Rate = k [A]^{x} [B]^{y} [C]^{z} \dots$

These exponents correspond to the rate-determining step in a multi-step mechanism and are found experimentally by measuring how rate varies with changes in reactant concentrations.

Rate law, rate constant

The rate law’s form, including exponents, must be determined from experimental data. The constant (k) is the rate constant, an empirically derived parameter that changes with reaction conditions (e.g., temperature).

Reaction order

The overall reaction order is the sum of all exponents in the rate law. A reaction can be:

Zero-order: The rate does not depend on reactant concentration (( $Rate$ = k)).
First-order: The rate depends on one concentration term to the first power.
Second-order: The rate depends on either one concentration squared or two separate concentrations multiplied.
Higher order: Combining multiple reactant concentration terms.

Rate-determining step

In a multi-step reaction, the slowest step is the rate-determining step. The overall reaction rate is controlled by this step, and the rate law is typically derived from its reactant concentrations.

Dependence of reaction rate upon temperature

The rate of a chemical reaction typically increases with temperature. As molecules gain thermal energy, collisions happen more frequently and with higher energy, making it more likely for them to surpass the energy barrier leading to the transition state.

Activation energy

The activation energy ( $E_{a}$ ) is the minimum energy needed for reactants to transform into products. A lower activation energy allows molecules to more easily reach the transition state, resulting in a faster reaction rate.

Activated complex or transition state

At the peak of the energy profile lies the transition state, which corresponds to an activated complex. Bonds forming and bonds breaking are partially in progress; the system can either revert to reactants or proceed to products. Unlike a stable reaction intermediate, the transition state exists momentarily and cannot be isolated.

Interpretation of energy profiles showing energies of reactants, products, activation energy, and $Δ$ H for the reaction

A reaction energy profile illustrates how energy changes along the reaction pathway:

The activation energy is the height from the reactant energy level to the transition state.
The enthalpy change ( $Δ$ H) is the difference between the energy of the products and the energy of the reactants:
- If $Δ$ H is negative, the reaction is exothermic.
- If $Δ$ H is positive, the reaction is endothermic.

Use of the Arrhenius equation

The Arrhenius equation relates the rate constant (k) to activation energy and temperature:

$k = A e^{- \frac{E _{a}}{RT}}$

where (A) is a constant, (E_a) is the activation energy, (R) is the gas constant, and (T) is the temperature. This equation reveals that lowering (E_a) or raising (T) increases (k), and thus accelerates the reaction.

Kinetic control versus thermodynamic control of a reaction

A reaction can yield multiple products under different conditions:

Kinetic product: Forms faster because it has a lower activation energy. Dominates at lower temperatures where reaction rates are paramount.
Thermodynamic product: More stable (lower free energy) but may require a higher activation energy. Dominates at higher temperatures or when the system is given enough time to reach the most stable state.

Catalysts and enzymes lower activation energy, accelerating both forward and reverse reactions without altering the overall thermodynamics. They do not change the position of equilibrium or the $Δ$ G of the process but enable the system to achieve equilibrium faster.

Catalysts

A catalyst speeds up a reaction by lowering its activation energy but does not shift the position of equilibrium. Catalysts accelerate both the forward and reverse reactions equally, allowing the system to reach the same equilibrium state more rapidly.

Equilibrium in reversible chemical reactions

Many reactions are reversible, meaning reactants can form products and products can revert to reactants. At equilibrium, the forward and reverse reaction rates are equal. While the concentrations of substances may remain constant at this point, reactions continue to occur in both directions at identical rates.

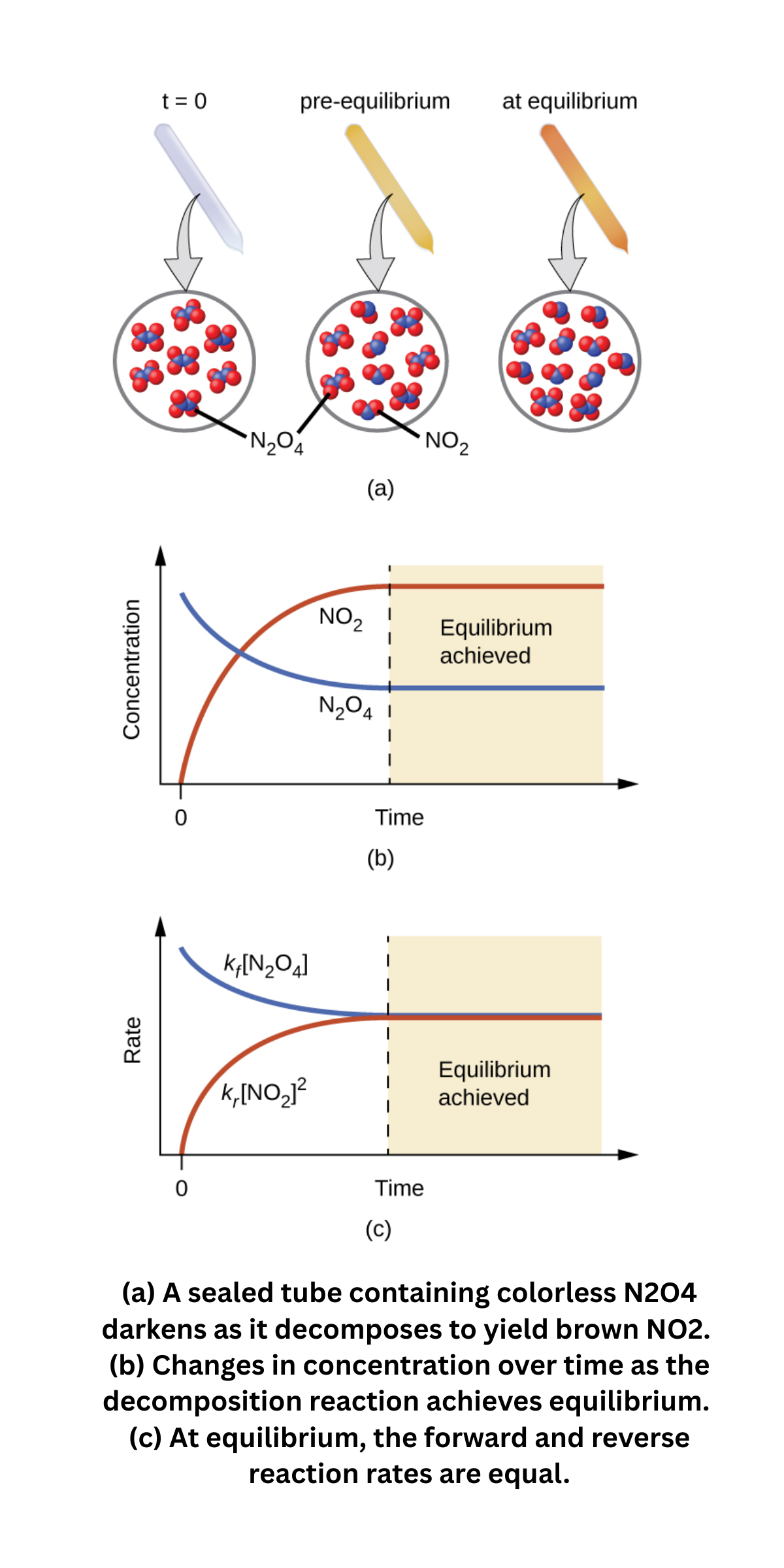
Chemical equilibrium in the reversible reaction N₂O₄ ⇌ 2NO₂

Law of mass action

This principle underlies how equilibrium constants are derived. It states that the rate of a reaction depends on the concentrations (or activities) of the reacting substances. For a generic reaction

$a A + b B \leftrightarrow c C + d D$

the equilibrium condition arises when the forward rate equals the reverse rate:

$k_{forward} [A]^{a} [B]^{b} = k_{reverse} [C]^{c} [D]^{d}$

This leads to the equilibrium constant ( $K_{e q}$ ):
$K_{e q}$ = $\frac{[ C ] ^{c} [ D ] ^{d}}{[ A ] ^{a} [ B ] ^{b}}$ .

Equilibrium constant

There are two primary ways to obtain ( $K_{e q}$ ):

From the balanced equation, applying the law of mass action.
From thermodynamics, using the standard free energy relationship:

$Δ G = Δ G^{\circ} + RT ln Q$

When ( $K_{e q}$ \gg 1), the reaction lies to the right (favoring products). When ( $K_{e q}$ \approx 1), the reaction balances between reactants and products. When ( $K_{e q}$ \ll 1), the reaction lies to the left (favoring reactants).

Application of Le Châtelier’s principle

If a system at equilibrium is disturbed, it will shift to re-establish equilibrium. Changes in concentration, pressure, volume, or temperature can push the reaction forward or backward. For instance, adding more reactant may push the reaction to produce more product, whereas increasing product concentration can drive the reaction back toward reactants.

Relationship of the equilibrium constant and $Δ$ $G^{\circ}$

Free energy ( $Δ G$ ) at any point in a reaction depends on the ratio of products to reactants (the reaction quotient $Q$ ):

$Δ G = Δ G^{\circ} + RT ln (Q)$

At equilibrium, $Δ G = 0$ and $Q = K_{e q}$ , thus:

$0 = Δ G^{\circ} + RT ln (K_{e q})$

leading to

$Δ G^{\circ} = - RT ln (K_{e q})$

Using standard enthalpy and entropy changes to calculate $Δ G^{\circ}$

Use standard enthalpy and entropy data from Appendix G to calculate the standard free energy change for the vaporization of water at room temperature (298 K). What does the computed value for $Δ G^{\circ}$ say about the spontaneity of this process?

Solution

The process of interest is the following:

$H_{2} O (l) \to H_{2} O (g)$

The standard change in free energy may be calculated using the following equation:

$Δ G^{\circ} = Δ H^{\circ} - T Δ S^{\circ}$

From Appendix G:

Substance	$Δ H_{f}^{\circ}$ (kJ/mol)	$S^{\circ}$ (J/K\cdot mol)
H $_{2}$ O(l)	$- 286.83$	$70.0$
H $_{2}$ O(g)	$- 241.82$	$188.8$

Using the appendix data to calculate the standard enthalpy and entropy changes yields:

$Δ H^{\circ} = Δ H_{f}^{\circ} (H_{2} O (g)) - Δ H_{f}^{\circ} (H_{2} O (l)) = [- 241.82 kJ/mol - (- 286.83 kJ/mol)] = 45.01 kJ$

$Δ S^{\circ} = 1 mol \times S^{\circ} (H_{2} O (g)) - 1 mol \times S^{\circ} (H_{2} O (l)) = (1 mol) \times 188.8 J/ (mol \cdot K) - (1 mol) \times 70.0 J/ (mol \cdot K) = 118.8 J/ (mol \cdot K)$

$Δ G^{\circ} = Δ H^{\circ} - T Δ S^{\circ}$

Substitution into the standard free energy equation yields:

$Δ G^{\circ} = 45.01 kJ - (298 K \times 118.8 J/K) \times \frac{1 kJ}{1000 J}$

$= 45.01 kJ - 35.4 kJ = 9.6 kJ$

At $298 K$ ( $25^{\circ} C$ ) $Δ G^{\circ} > 0$ , so boiling is nonspontaneous (not spontaneous).

Adapted from Example 12.7, OpenStax

Rate processes in chemical reactions - Kinetics and equilibrium