Stoichiometry

Molecular weight and formula, common metric units in chemistry

Molecular weight is numerically equivalent to the molecular mass of a substance and is measured in amu. Since 1 amu is defined as 1 $g/mol$, an element like Oxygen-16, with a mass of 16 amu, weighs 16 $g/mol$. The molecular formula of a compound, such as glucose ($C_6{H}_{1}2O_6$), specifies the exact number of each type of atom present, while the empirical formula represents the simplest whole-number ratio of these atoms (for glucose, $C{H}_{2}O$).

In chemistry, we often use metric units like molarity ($M=mol/L$) to express concentration and molality ($m=mol/kg$) to denote the number of moles per kilogram of solvent, with molar mass expressed in $g/mol$ and overall mass measured in kilograms.

Composition by percent mass, mole concept, density

• % Mass represents the proportion of a specific species’ mass relative to the total mass of a sample, calculated as (% mass = [mass of species / total mass] × 100).\
• The mole concept helps in quantifying substances at the molecular level, where 1 mole equals Avogadro’s number (approximately $6.02\times 10^{23}$ molecules).\
• Density is defined as the mass per unit volume (density = mass/volume, measured in $kg/m^3$), and in chemistry, specific gravity is often used. Specific gravity is the ratio of the density of a substance to that of water (density of water = 1 $g/ml$ or 1 $g/c{m}^3$), making it a unitless measure; for example, if lead has a density of 11 $g/c{m}^3$, its specific gravity is 11.

Oxidation number

The oxidation number of an atom is the charge it would carry if the compound were entirely composed of ions.

Oxidizing agents are substances that gain electrons during a redox reaction, thereby causing another substance to be oxidized. Common examples include oxygen ($O_2$), ozone ($O_3$), permanganates ($Mn{O}_4^{-}$), chromates ($Cr{O}_4^{2-}$), dichromates ($C{r}_2{O}_7^{2-}$), and peroxides ($H_2{O}_2$), as well as various Lewis acids or compounds rich in oxygen. These agents have a high electron affinity and typically increase their oxidation state by accepting electrons.

In contrast, reducing agents donate electrons and are thus responsible for reducing other species. Typical reducing agents include hydrogen ($H_2$), reactive metals such as potassium, and reducing mixtures like $Zn/HCl$ and $Sn/HCl$, along with strong reductants like LAH (Lithium Aluminum Hydride) and $NaB{H}_4$ (Sodium Borohydride), as well as various Lewis bases or hydrogen-rich compounds. These agents tend to lower their oxidation state by losing electrons.

An important concept in redox reactions is disproportionation, where a single element in one oxidation state simultaneously undergoes both oxidation and reduction. For example, in the reaction $2C{u}^{+}\to Cu+C{u}^{2+}$, the $C{u}^{+}$ ion acts as both the oxidizing and reducing agent: one $C{u}^{+}$ loses an electron to become $C{u}^{2+}$; the other gains an electron to form elemental copper ($Cu$).

Redox titration

Redox titration is an analytical technique used to determine the concentration of an unknown analyte by reacting it with a known titrant that participates in a redox (reduction-oxidation) reaction. In these processes, the analyte can exist in a reduced form (A_red) or an oxidized form (A_ox), while the titrant is chosen as either a strong oxidizing agent (T_ox) or a reducing agent (T_red), depending on the nature of the analyte. Often, a standard solution with an accurately known concentration is used to calibrate the reaction, ensuring precise quantification.

A common variant is iodimetric titration, where the redox reaction involves iodine ($I_2$). For instance, a reduced analyte reacts with iodine to yield its oxidized counterpart along with iodide ions ($I^{-}$). In more complex procedures, an intermediate species ($X$), which can be in an oxidized ($X_{\mathrm{ox}}$) or reduced ($X_{\mathrm{red}}$) state, is formed and later reacts with the titrant. The endpoint of the titration is typically detected by a distinct color change; for example, iodine forms a dark blue complex with starch that disappears when all the iodine is reduced, signaling the completion of the reaction. This technique is analogous to acid-base titration but focuses on changes in oxidation states rather than pH shifts, making it a versatile method for quantifying substances that undergo redox reactions.

Description of reactions by chemical equations

A chemical equation is written according to specific conventions that communicate both the reactants and products along with their respective phases—(s) for solids, (l) for liquids, (g) for gases, and (aq) for aqueous solutions.

• Coefficients are placed before each compound to ensure the equation is balanced, meaning the number of atoms for each element is conserved on both sides.
• The arrow in the equation indicates the direction of the reaction: a single-headed arrow signifies a reaction that goes to completion, while a double-headed arrow denotes an equilibrium; if one side of the double arrow is larger, the equilibrium favors that side.
• The charge on ions is also indicated, with symbols such as + or -, while neutral species are left without a charge.

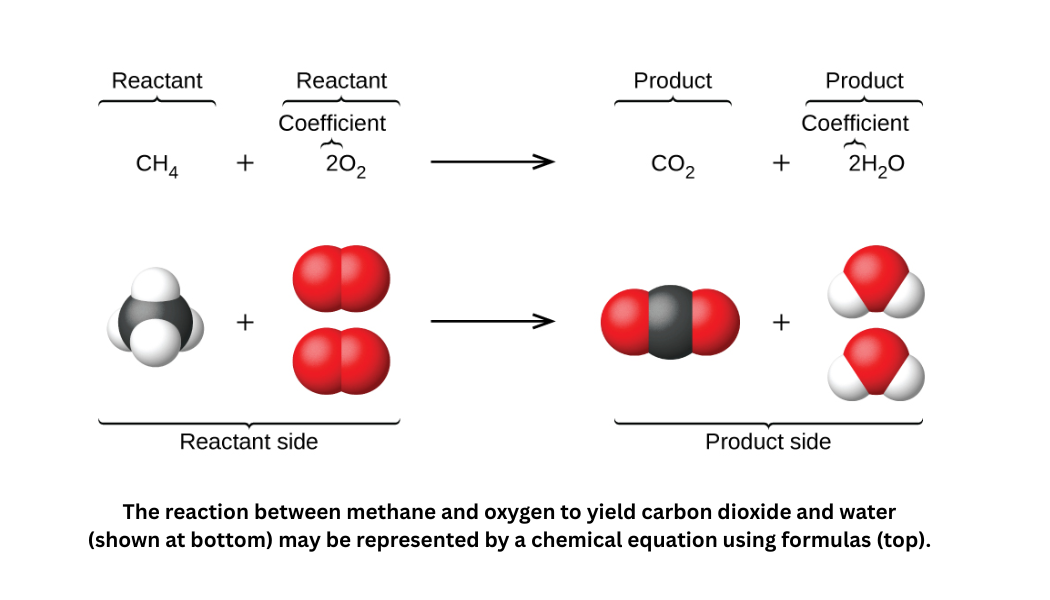
To balance chemical reactions:

1. start by balancing each of the half reactions separately, ensuring that both the atoms and charge are equal on both sides.
   • Under acidic conditions, balance oxygen atoms by adding $H_{2}O$ to the side that needs oxygen, and then add $H^{+}$ to the opposite side to balance the added hydrogen atoms.
   • Under basic conditions, add $2O{H}^{+}$ to the side lacking oxygen and then add $H_{2}O$ to the other side to balance the hydrogens. Two common methods used are the Ion-Electron Method, which balances atoms first and then charge, and the Oxidation-State Method, where you treat the species undergoing a change in oxidation number as a single entity.
2. Once the half reactions are balanced, multiply them by appropriate factors so that the electrons cancel out when you add the equations together.
3. Finally, combine identical species on the same side, cancel out any species that appear on both sides, and add back any spectator ions. Ensure that the final equation has the same number of each atom on both sides and a neutral net charge.

Limiting reactants and theoretical yields

The limiting reactant is the substance that is completely consumed first in a chemical reaction, thereby determining the maximum yield of products.

The theoretical yield is the maximum amount of product predicted by stoichiometry under ideal conditions. To calculate it, you first determine the limiting reactant—the substance that will be completely consumed—and then use its stoichiometric relationship to find the expected amount of product. The percent yield is then calculated by dividing the experimental yield (the actual amount obtained) by the theoretical yield and multiplying by 100. In practice, the experimental yield is usually lower than the theoretical yield due to losses during the reaction process.

Calculation of percent yield

Upon reaction of 1.274 g of copper sulfate with excess zinc metal, 0.392 g copper metal was obtained according to the equation:

$$\mathrm{CuS}{\mathrm{O}}_4(\mathrm{aq})+\mathrm{Zn}(\mathrm{s})\to \mathrm{Cu}(\mathrm{s})+\mathrm{ZnS}{\mathrm{O}}_4(\mathrm{aq})$$

What is the percent yield?

The provided information identifies copper sulfate as the limiting reactant, and so the theoretical yield is found by the approach illustrated in the previous module, as shown here:

$$1.274{\cancel{\text{g CuSO}}}_4\times \frac{1{\cancel{\text{mol CuSO}}}_4}{159.62{\cancel{\text{g CuSO}}}_4}\times \frac{1\cancel{\text{mol Cu}}}{1{\cancel{\text{mol CuSO}}}_4}\times \frac{63.55\text{g Cu}}{1\cancel{\text{mol Cu}}}=0.5072\text{g Cu}$$

Using this theoretical yield and the provided value for actual yield, the percent yield is calculated as:

$$\text{percent yield}=\left(\frac{\text{actual yield}}{\text{theoretical yield}}\right)\times 100$$

$$\text{percent yield}=\left(\frac{0.392\text{g Cu}}{0.5072\text{g Cu}}\right)\times 100=77.3\%$$