Short puts
This chapter covers the fundamentals of short put options contracts. To gain a good understanding of the language used when discussing options, watch this video:
When an investor goes short a put, they are bullish on the underlying security’s market price. Selling a put obligates the investor to buy stock at the strike price if assigned (exercised). If the stock’s market price falls below the put’s strike price (“put down” - the put is “in the money”), the holder may exercise the option, forcing the writer to fulfill their obligation. If the market price rises above the strike price (the put is “out of the money”), the holder will not exercise the option, and the writer realizes a gain equal to the premium.
Let’s work through a few examples to understand short puts better:
Short 1 ABC Sep 75 put @ $6
This contract obligates the writer to buy ABC stock at $75 per share if assigned. The writer received $600 for selling the option ($6 premium x 100 shares), which expires on the third Friday in September. The investor is betting ABC stock’s market price stays at or above $75 before expiration. Otherwise, the holder will exercise the option, resulting in losses for the writer.
Math-based options questions should be expected on the exam. Normally, they involve potential gains, losses, and breakeven values. Let’s go through each.
An investor goes short 1 ABC Sep 75 put @ $6. The market price falls to $0. What is the gain or loss?
Can you figure it out?
Answer = $6,900 loss
| Action | Result |
|---|---|
| Sell put | +$600 |
| Assigned - bought shares | -$7,500 |
| Share value | +$0 |
| Total | -$6,900 |
At $0, the option is $75 “in the money.” This is the worst-case scenario for a put writer. We can safely assume the investor was assigned their contract, requiring a purchase of 100 ABC shares at $75. The shares are worthless, so the investor experiences a $75 loss per share. The assignment results in a $7,500 loss ($75 loss x 100 shares). Factoring in the $600 premium received upfront brings the overall loss down to $6,900.
The maximum loss for a short put can be found by utilizing this formula:
The strike price of $75 minus the premium of $6 leaves the investor with a maximum loss of $69 per share (or $6,900 overall).
In the short call chapter, we learned an option is “naked” when sold without a hedge (protection). The same applies to a short put. As you’ve learned, a short put is risky because it may result in the investor buying shares at the higher strike price when their market values are lower. In the worst-case scenario, the investor is forced to purchase worthless shares at the strike price.
In the next chapter, you’ll learn how investors protect themselves from risk on short options. For now, here is a quick list of investments that would cover a short put:
- Short shares
- Long put
- Cash (equal to the maximum loss)
The risk of a short put comes from selling shares at a lower price (or not being able to sell shares because they’re worthless) compared to what they were bought for when assigned. If the investor is short the shares, the sale already occurred. When the put is assigned, the customer effectively “buys back” the short shares, which closes their position. They won’t have to worry about selling them at a lower price because the sale already occurred when the stock was sold short!
If the investor owns a put (in addition to the short put), they maintain the right to sell the shares purchased at assignment at the long put’s strike price. Even if the market price drops dramatically, they can exercise the long put and sell the shares at a higher strike price.
While cash does not prevent losses, posting cash in an account equal to the maximum loss of a short put technically “covers” the put. The investor has more than enough money to pay for the short put’s risk; therefore, the short put is covered. Remember that cash cannot cover a short call because its risk is unlimited.
Let’s look at an example that is more likely to occur:
An investor goes short 1 ABC Sep 75 put @ $6. The market price falls to $60. What is the gain or loss?
Answer = $900 loss
| Action | Result |
|---|---|
| Sell put | +$600 |
| Assigned - bought shares | -$7,500 |
| Share value | +$6,000 |
| Total | -$900 |
The market price fell to $60 and the option went “in the money” by $15. This is not good for the writer! After being assigned, they must buy 100 ABC shares for $75. The shares are only worth $60, which locks in a $1,500 loss ($15 loss x 100 shares). Factoring in the $600 premium received up-front reduces the overall loss to $900.
Investors who sell puts don’t always lose money. Even if ABC’s market price falls below $75, the seller must lose at least an amount equal to the premium to have an overall loss.
Let’s work through another example.
An investor goes short 1 ABC Sep 75 put @ $6. The market price falls to $69. What is the gain or loss?
Answer = $0 (breakeven)
| Action | Result |
|---|---|
| Sell put | +$600 |
| Assigned - bought shares | -$7,500 |
| Share value | +$6,900 |
| Total | $0 |
At $69, the option is $6 “in the money.” The option gained intrinsic value, but the writer didn’t lose enough money from the assignment to have an overall loss. The investor was forced to buy ABC stock at $75 when the shares were only worth $69, resulting in a $600 loss ($6 loss x 100 shares). The $600 premium received upfront offsets the assignment loss, and the investor breaks even.
When investing in puts, the breakeven can be found using this formula:
You probably noticed, but this is the same breakeven formula for long puts. With the two sides acting as opposites, it shouldn’t be a surprise they both get back breakeven at the same point. With a strike price of $75 and a premium of $6, the investor breaks even when ABC stock is at $69 per share. At this market value, there is no profit or loss.
The breakeven formula is also same as a short put’s maximum loss formula. Regardless, the maximum loss must be multiplied by 100 to show the overall loss covering 100 shares (on a per contract basis). Breakeven only refers to the market price of ABC, which is why you don’t need to multiply by 100.
If ABC’s market price doesn’t fall too far below $75, the investor could make a profit. For example:
An investor goes short 1 ABC Sep 75 put @ $6. The market price falls to $74. What is the gain or loss?
Answer = $500 gain
| Action | Result |
|---|---|
| Sell put | +$600 |
| Assigned - bought shares | -$7,500 |
| Share value | +$7,400 |
| Total | +$500 |
At $74, the option is $1 “in the money.” The assignment resulted in a $1 per share loss as the investor was forced to buy 100 ABC shares at $75 that were only worth $74. The overall loss from the assignment was $100 ($1 x 100 shares). When the upfront $600 premium received is included, the investor achieves an overall gain of $500.
Expiration is the best-case scenario for investors writing (going short) options. When this occurs, the investor receives a premium for an option that is never used (the obligation is not required to be fulfilled). The same applies to short put contracts.
An investor goes short 1 ABC Sep 75 put @ $6. The market price rises to $84. What is the gain or loss?
Answer = $600 gain
| Action | Result |
|---|---|
| Sell put | +$600 |
| Total | +$600 |
At $84, the option is $9 “out of the money” and has no intrinsic value. When the market price is above $75, the holder does not exercise their option. Why would they exercise and sell the stock for $75 when the market is trading it for $84? At this point, the option expires worthless.
An easy way to determine if a put will be assigned is utilizing the phrase “put down.” Puts are only exercised if the underlying security’s market price is below the strike price. This is not the case in this example, so the option expires.
Investors with short options can only make the premium, nothing more. It only goes downhill from there. If an exercise occurs, losses will start eating away at the premium, potentially pushing the investor to a loss.
Writers can also perform closing transactions to exit their obligations before expiration.
An investor goes short 1 ABC Sep 75 put @ $6. After ABC’s market price rises to $79, the premium falls to $2, and the investor does a closing purchase. What is the gain or loss?
Answer = $400 gain
| Action | Result |
|---|---|
| Sell put | +$600 |
| Close put | -$200 |
| Total | +$400 |
To find the profit or loss for a closing transaction, we’ll compare the premium received for selling the option to the premium paid for closing it out. When the put was initially sold, the premium was $6. The market price increased, causing the option’s premium to fall. When the option contract was bought (closing purchase), the premium was $2. This results in a $4 net gain (credit).
With option premiums representing 100 shares, the investor has a $400 overall gain.
Here’s a visual summarizing the important aspects of short puts:
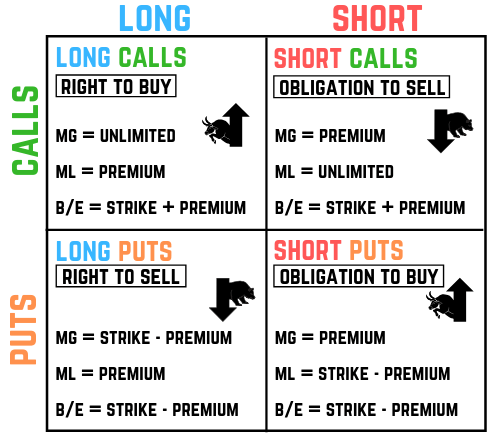
You’ve now been through all four versions of options: long calls, short calls, long puts, and short puts. The following visual puts it all together:
Sign up for free to take 22 quiz questions on this topic