A trend is a pattern in a graph or table of data. On the ACT test, trends are usually used to relate two different sets of data. Questions that ask about the trends of data are extremely common in the science section of the test, so make sure you are comfortable with these ones!
Let’s first take a look at how to recognize trends in both tables and graphs. Then, we will look at what we can do with those trends.
When looking for trends in tables, we are usually only looking at two columns of data. Even if the table has many columns, the question will typically only have you compare two of them. So, let’s see what this looks like. The example below will have the columns and for simplicity:
| 1 | 5 |
| 2 | 10 |
| 3 | 15 |
| 4 | 20 |
| 5 | 25 |
As the values increase, the values also increase. This would be the trend that describes this table. If you feel comfortable with this simple trend, try indicating the claim in the next example.
| Temperature (º) | Density (m3/kg) | Viscosity (mm2/s) | Vapor Pressure (kPa) |
| 15 | 1.004 | 1.3 | 1.74 |
| 20 | 1.000 | 1.1 | 2.35 |
| 25 | 0.998 | 1.0 | 3.16 |
| 30 | 0.994 | 0.8 | 4.19 |
| 35 | 0.990 | 0.5 | 5.52 |
As temperature increases, what happens to the viscosity of the chemicals?
Give it a try, and then check our explanation!
As temperature increases (from to ), viscosity decreases (from to ).
There are many columns, but we only need to focus on the ones mentioned in the question: temperature and viscosity. We observe the trend by moving down the table for each column.
Find trends in graphs by looking at a line or set of dots and figuring out the direction that they move. As the axis increases, does the line move upward or downward? In other words, do the values increase or decrease?
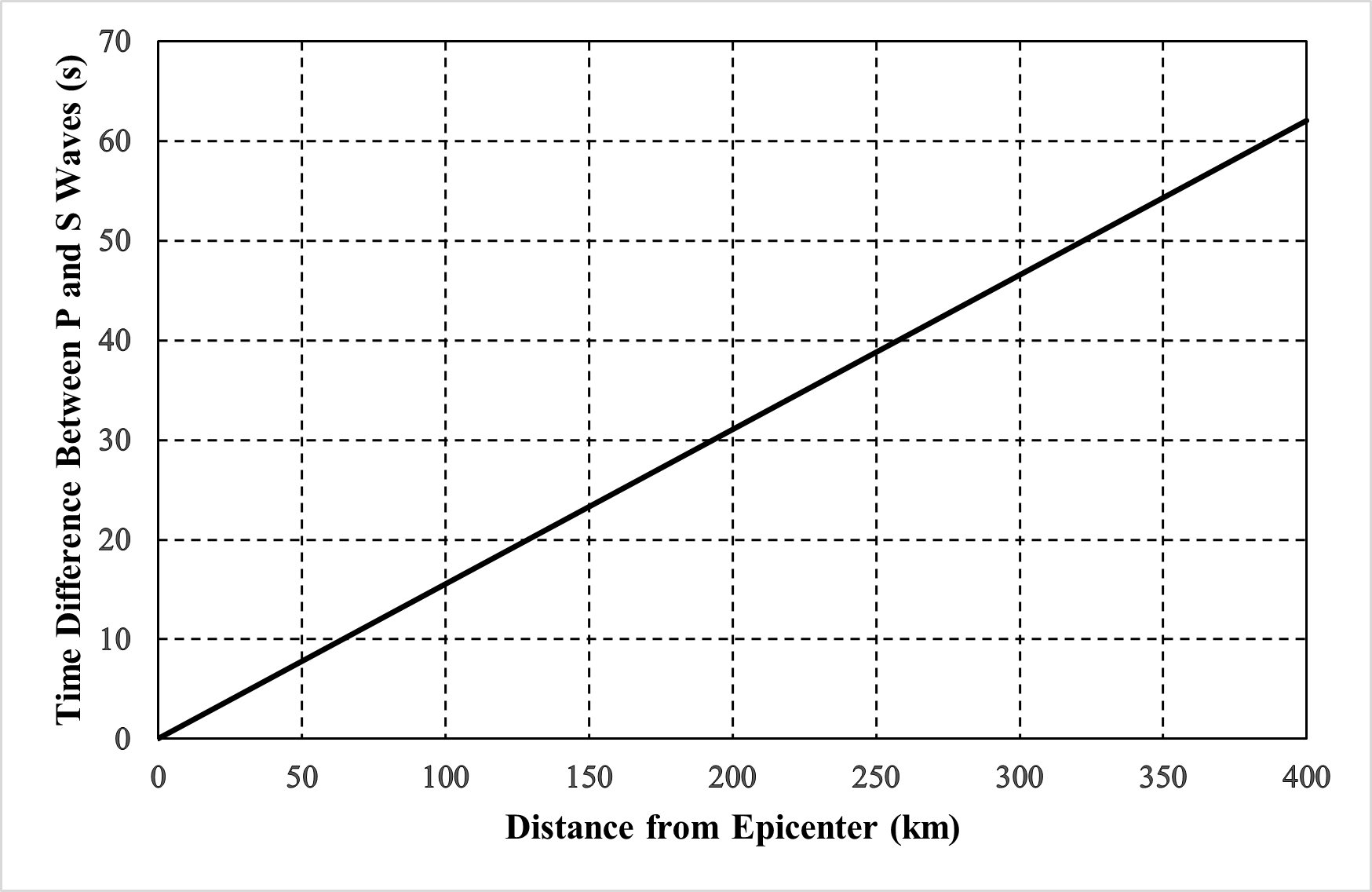
For this line, we can see that as we move along the axis the line gets higher. This means that as increases, increases. In terms of this graph, “as the distance from the epicenter increases, the time difference between P and S waves also increases.”
Graphs with multiple lines will not always follow the same trend. Sometimes one line increases with and the other line decreases with . Make sure that you are looking at the trend for the correct line that the question is asking about.
Some questions will have you estimate where a line would end up on a graph, or where a number might go on a table, based on the trend of the figure. For instance, the graph above ends when is equal to km. A question along these lines might ask you to predict what the time difference between P and S waves would likely be when the distance from the epicenter is equal to km. There are a few ways to do this.
First, you may solve this the quick way (recommended) though it will not be perfect. This method is done by simply mimicking the trend of the line and literally drawing the rest of the line past where it ends on the graph. This is an estimation of where it would end up, judging just by how it looks like it is moving.
Second, you may solve this problem by looking at how much the line is increasing as it ends. In our case, since we want to find the point 100 km after the graph ends, we want to know how much it will grow in km. So, we should measure how much it grew in the last km (from to ). Let’s look at the graph again so we can make sense of this:
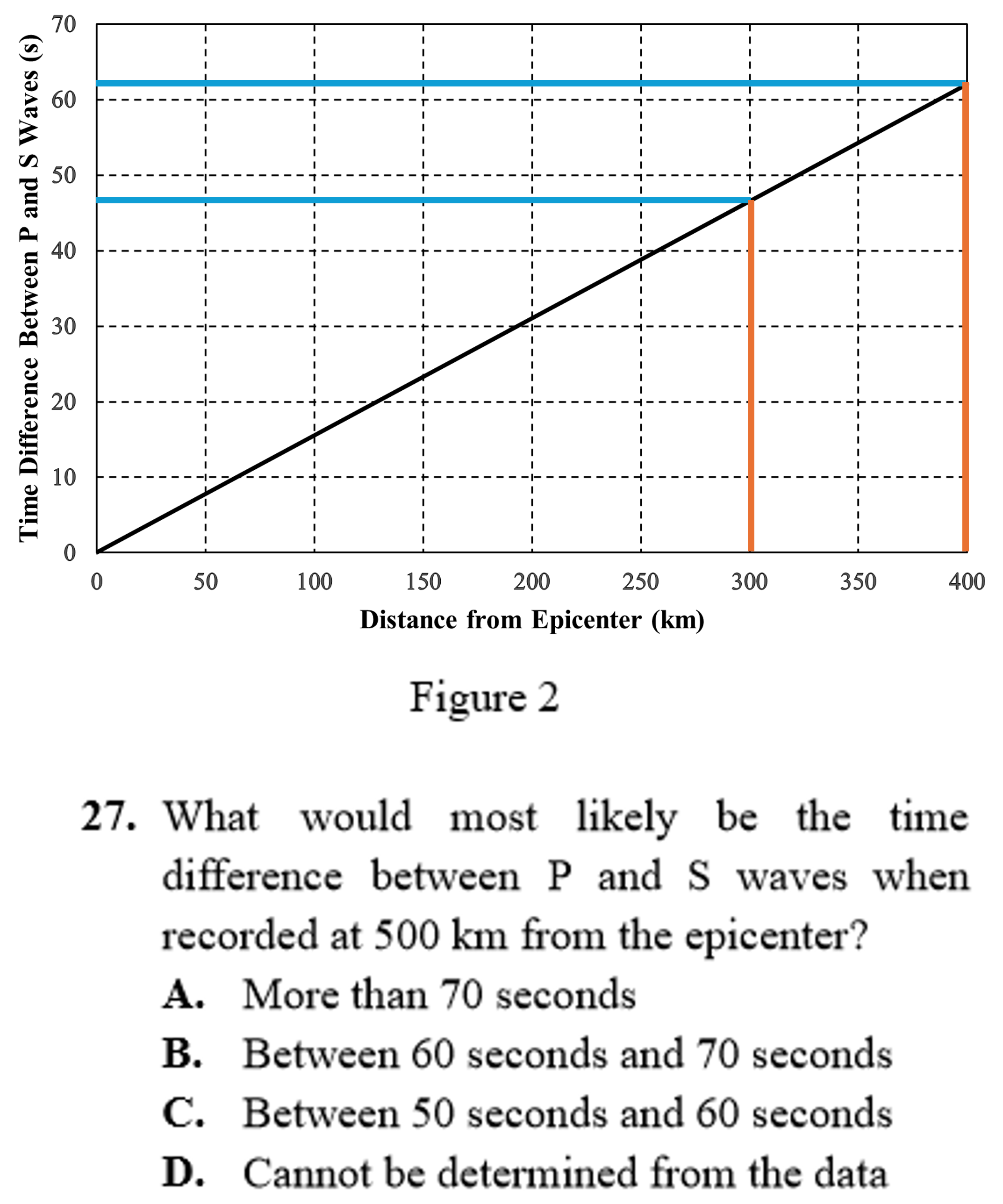
The line increases by about seconds on the axis from to (indicated by the blue lines) when the axis increases by from to (indicated by the red lines). Apply this number to the final point on the graph to predict what the concentration would be at a distance of km ( km after the graph ends): .
Regardless of the method you choose, your goal is to predict where the line would be if the graph extended as far as the question mentions. As long as you are able to confidently predict this, you will do fine on these questions.
Sign up for free to take 5 quiz questions on this topic