Absolute value | Pre-algebra | ACT Math

Absolute value is easy to identify because it uses |these vertical lines| in expressions. The rules are relatively simple. So, even if a question seems difficult, don’t get discouraged! Remember this one key rule: after everything is settled inside absolute value signs, everything becomes positive.

Let’s look at the absolute value of some numbers:

$∣2∣$ , i.e., the absolute value of $2$ , simplifies to the number $2$ .
$∣$ $- 2∣$ , i.e., the absolute value of $- 2$ , must follow our rule: everything on the inside becomes positive. It also simplifies to $2$ .

But not everything is this easy. It can get a bit more algebraic:

How about $3 - ∣2 - 6∣$ ? Remember PEMDAS, and treat absolute value as parentheses. First solve what is inside the absolute value signs: $∣2 - 6∣ = ∣$ $- 4∣$ then perform the absolute value rule: $∣$ $- 4∣ = 4$ finally, finish out the rest of the expression: $3 - 4 = - 1$ Here, the answer is negative overall, but the number we get from the absolute value signs ( $4$ ) is positive because our absolute value numbers should always come out positive. After all, that is the rule.

Layered absolute value questions

This question is an example of an absolute value within another absolute value. Try this one on your own, applying the same rule we discussed:

$∣3 - ∣5 - 3 (12) ∣∣$

(spoiler)

Like with PEMDAS, we start with the innermost parentheses or absolute value sign and work outward:

$∣3 - ∣5 - 3 (12) ∣∣ ∣3 - ∣5 - 36∣∣ ∣3 - 31∣ ∣ - 28∣ 28$

As you see, we treat absolute value signs exactly as we would if they were parentheses, solving them in order of innermost to outermost, but we make sure to add in the step of making the final number positive after each one.

Absolute value solutions

There are some questions that you should be familiar with that ask you to find solutions to an equation, meaning you need to find a value for $x$ that makes the equation true.

If $x$ is within the absolute value lines, it adds a new step when doing these problems by adding an extra solution to the equation, which you can see below:

Find the solutions to the following equation: $4 + ∣ x - 12∣ = 12$

The first thing we should do is move the things from the left side so all we have is the absolute value on the left. So, we subtract $4$ from both sides. Then, $∣ x - 12∣ = 8$ .

At this point we need to recognize a key principle: the value within the absolute value signs can be either positive or negative. When you remove the absolute values in your algebra steps, be sure to write out the insides as positive and as negative:

$(x - 12) = 8 and - (x - 12) = 8$

So, try to solve this yourself. Remember, there are two solutions.

(spoiler)

$∣ x - 12∣ = 8$

$x - 12 = 8 and - (x - 12) = 8$

Let’s solve the left (positive) equation first, by adding $12$ to both sides:

$x = 20$ for the left equation. The right equation will take some more work.

We first need to distribute the negative sign throughout the parentheses so our new equation becomes $- x + 12 = 8$ .

We then add over the $x$ , then subtract $8$ , getting $12 - 8 = x$ or $4 = x$ .

$x = 20 and x = 4$

We can check this by plugging in these solutions to the original equation:

$4 + ∣20 - 12∣ 4 + ∣8∣ 12 = 12 = 12 = 12$

$4 + ∣4 - 12∣ 4 + ∣ - 8∣ 4 + 8 = 12 12 = 12 = 12 = 12$

Absolute value graphs

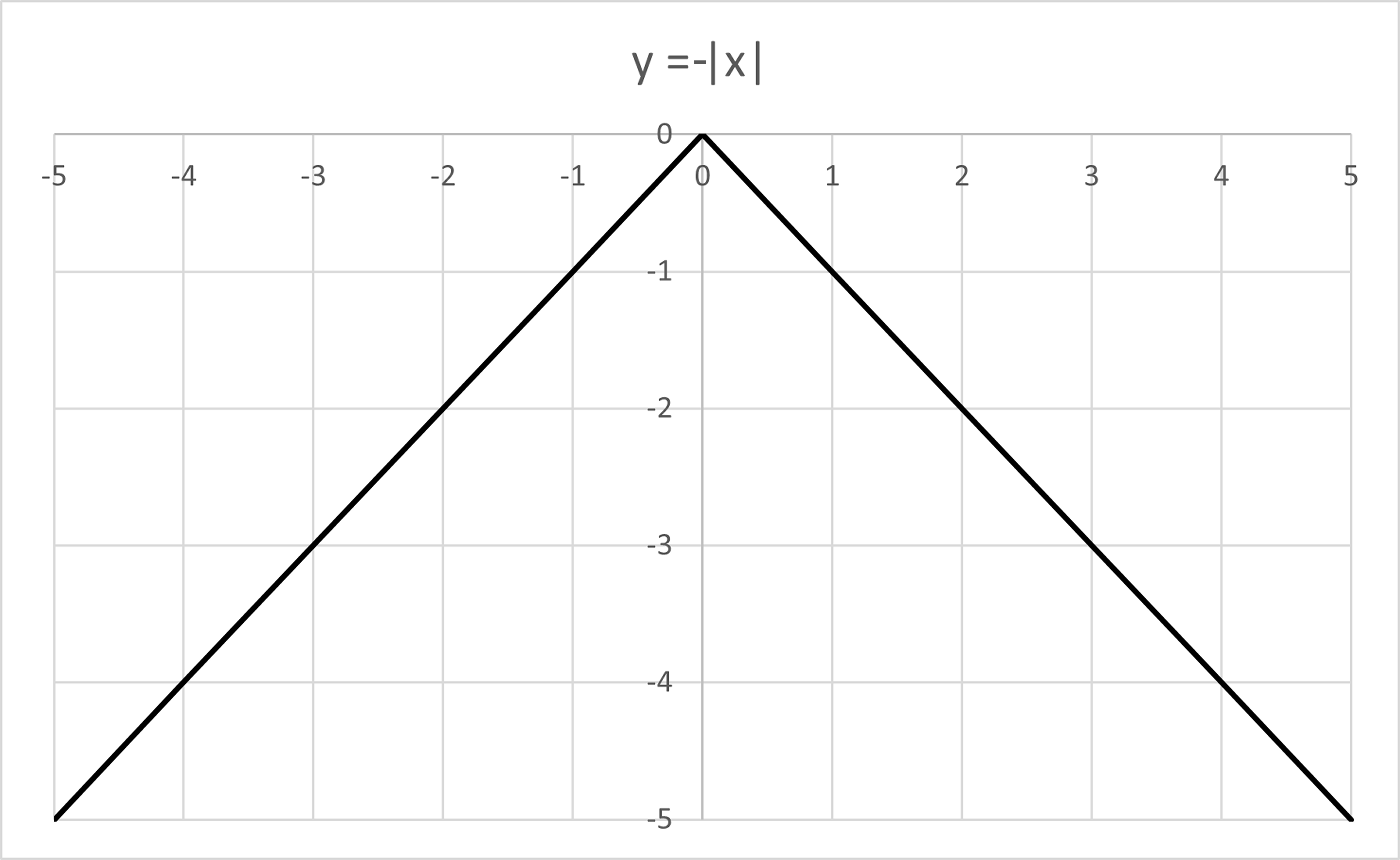
There is one important trait you need to recognize when it comes to absolute value graphs: the way it looks. Absolute value graphs look like a “V” whether right side up or upside down:

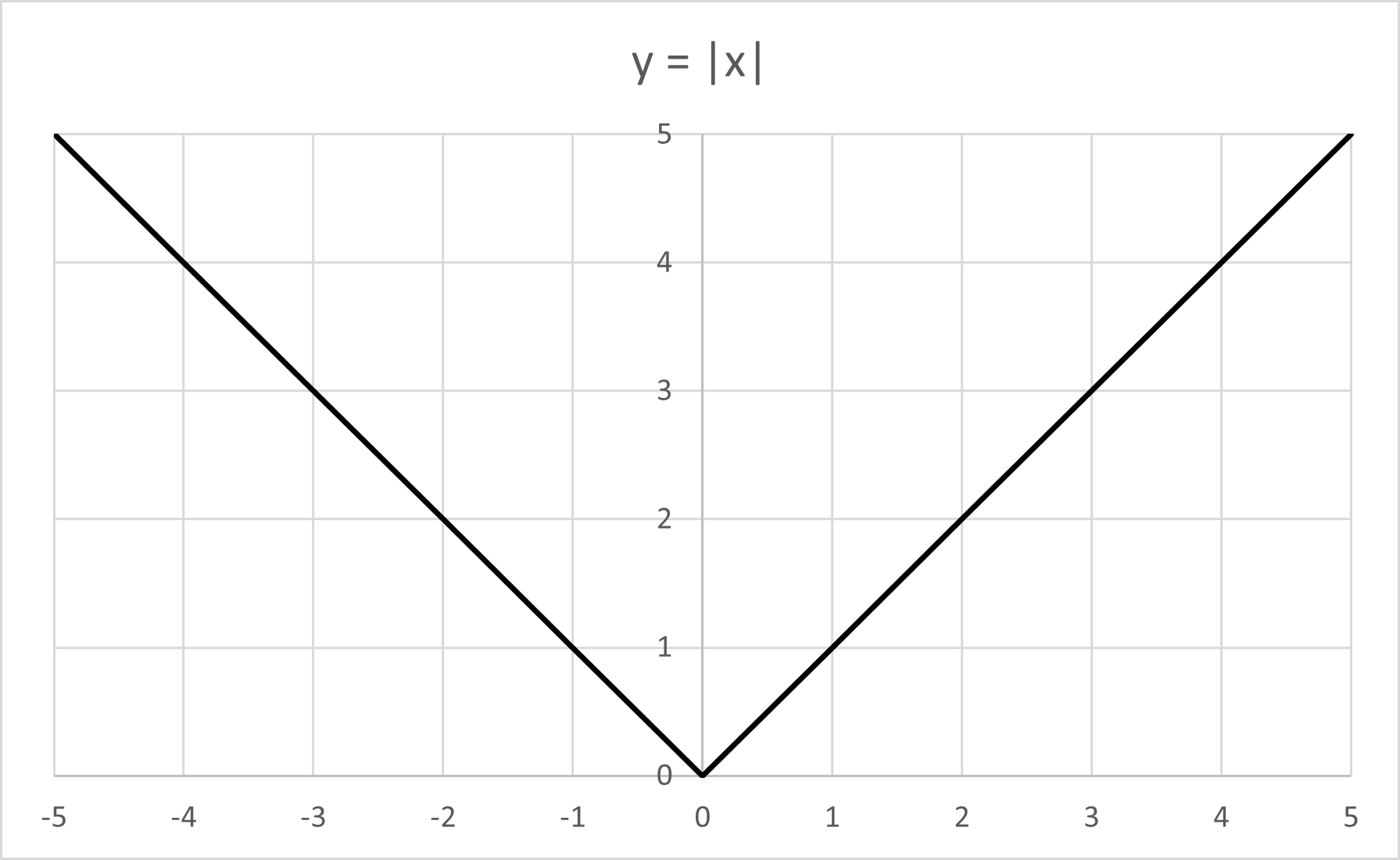
$Absolute value facing up$

$Absolute value facing down$

Key points

Notation. Absolute value is denoted by |these vertical lines|.

Primary rule. The final value within absolute value lines becomes positive.

Layered questions. Follow the order of PEMDAS as if absolute value lines were parentheses: do them first, working from the inside to the outside.

Multiple solutions. Absolute value equations have multiple solutions if $x$ is within the lines. The final value inside the absolute value lines can be either positive or negative because it will become positive after applying the primary rule.

Graphs. Remember that an absolute value graph looks like a V.