Logic questions are part of the quantitative reasoning section much more for their reasoning emphasis than for their quantitative emphasis, though they may have quantitative parts as well. These questions generally require reading and combining statements to discover what inferences may be made. Propositional, or formal, logic constitutes a significant subcategory of logic questions.
Here’s a sample question:
Josh has chemistry class on every day on which he has a biology lab. Chemistry tests replace a regular chemistry class on Friday every other week. If Josh has his chemistry class on Mondays, Wednesdays, and Fridays only, which of the following, if any, must be true?
I. Josh has biology lab on Mondays, Wednesdays, and Fridays.
II. Josh has a chemistry test on Friday this week.
III. Josh never has biology lab on Thursdays.A. I only
B. III only
C. II and III only
D. None of the above must be true.
Consider the question and, when you’re ready, read the explanation below.
Logic questions present two primary tasks: first, combining statements to draw logical inferences, and second, employing the tools of conditional, or formal, logic. Let’s take these one at a time as they relate to this question.
There is a statement in the question relating biology lab to chemistry class, a statement relating chemistry tests to chemistry class, and a final statement identifying the scheduled days for chemistry class. The first statement can be summarized as follows: A day that has a biology lab must also have a chemistry class, but the reverse is not necessarily true (for reasons we’ll see below). We then learn of a (sometimes) replacement: every other week, Friday’s chemistry plan is a test instead of a class.
Now let’s consider the first statement more closely. It is a universal (all or nothing) declarative statement, also known as a proposition. All such statements can be converted into “If, then” format, where the content of the “if” clause always leads to the outcome described in the “then” clause. In this case, the “if/then” translation would be: If Josh has a biology lab on a certain day, then he also has chemistry class on that day. Based on the information given, this statement is universally true for Josh’s current class schedule.
This kind of statement raises three questions that students of propositional logic will be familiar with.
The first of these “if” statements is called the converse; it reverses the clauses without negating them. Formal logic tells us that the converse is an invalid inference from the original statement. That means that it may be true, but that it does not follow logically. Take a moment to look at the original question. If you think about the first sentence carefully, you may see that having a chemistry class doesn’t require Josh to have a biology lab on that day as well. If we see Josh walking to his chemistry class (and either envy Josh or pity him, depending on how we feel about chemistry), we can suppose that he might also have lab on that day, but we can’t know for sure.
The second question above shows the inverse of the original statement; it negates both clauses without reversing them. Like the converse, the inverse is not a logically valid inference. In this case, if Josh doesn’t have biology lab, that doesn’t mean he doesn’t have his chemistry class. Put another way, the original sentence leaves open the possibility that Josh’s chemistry class meets on more days per week than does his bio lab. If Josh tells us with a sigh (of either relief or disappointment), “I don’t have bio lab today,” we won’t, from that statement alone, have either idea whether his chemistry class meets on that same day.
Question #3 above constitutes the logical contrapositive; unlike the converse and inverse, the contrapositive is a universally valid logical inference. To explore this, consider the original statement again. If we meet Josh on the way to his biology lab, that means he must also have chemistry class on that day. But for this reason, if we run across him bemoaning (or relishing) the lack of chem class on a particular day, there’s no way he can have the bio lab on that day, because if he has the lab, he must have the chemistry class as well!
At this point, you might be understandably lost in a haze of words. Propositional logic is not easy to explain in words and can be more succinctly demonstrated in a diagram (which is why it is also called “formal” logic, that is, logic according to form). Here’s a diagram that shows both Josh’s real-life situation and a more abstract picture that shows in a universal way how this kind of logic works.
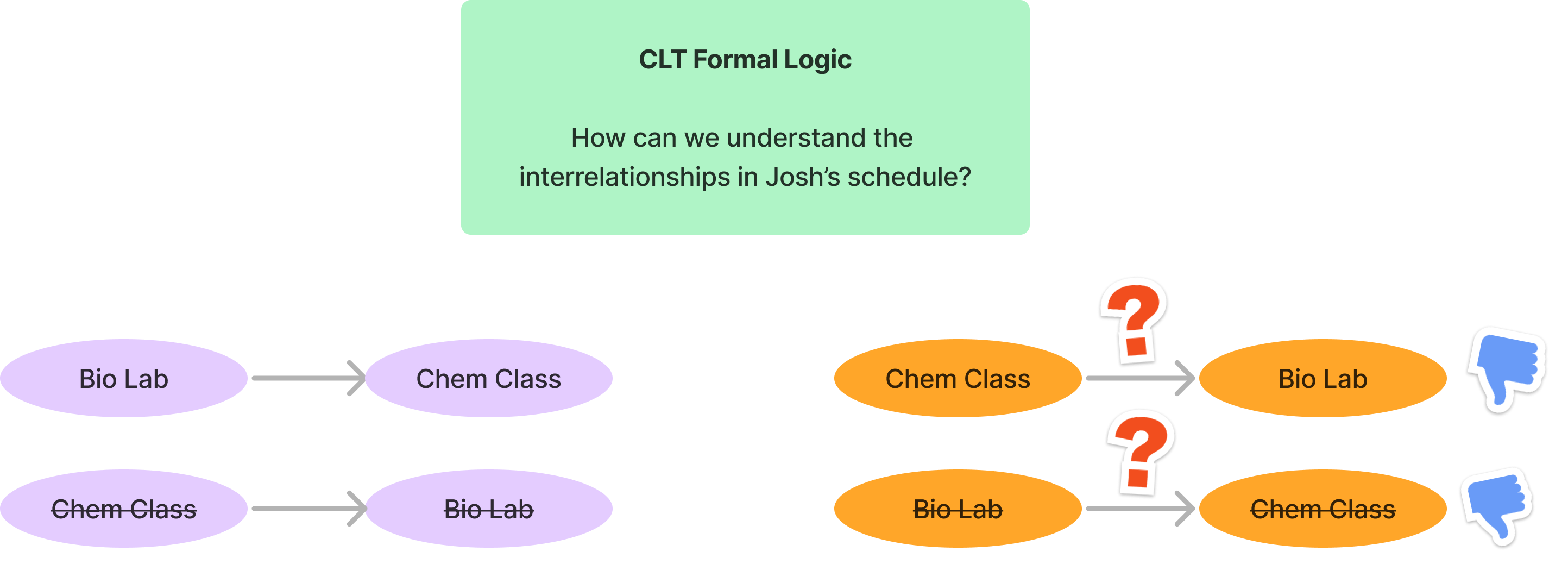
With this all in mind, we conclude that only statement III must be true. If Josh had a biology lab on Thursdays, then he would have a chemistry class on that day as well. But his chemistry class only meets on Monday, Wednesday, and Friday. The answer is B.
Instead of universal formal logic statements, the CLT may, on rare occasions, present you with questions involving particular (limiting) words like “most” or “some”.
You do not need to make many flashcards related to logic questions, but if you are not familiar with any of the key terms in this module, making flashcards with the term and definition would be a good idea.
At the Lyceum School, the sports offered for girls in the spring are tennis, softball, and track. No student may participate in both tennis and softball due to scheduling conflicts, but track may be pursued alongside either of the other two sports. If Corinne wants to do at least one spring sport but does not participate in track, which of the following must be true?
A. Corinne participates in tennis.
B. Corinne participates in tennis and softball.
C. Corinne participates in softball.
D. Corinne participates in only one spring sport.
The answer is D. Let’s start with the fact that Corinne does not participate in track, since that fact is mentioned last, and work backward. What else do we know about track? It’s the most flexible sport, schedule-wise; track and be done alongside tennis or softball, but tennis and softball together a no-go. So if Corinne doesn’t participate in track, there are only two sports left, and they can’t both be joined. Choice D is true, while choice B is outright false; choices A and C, while they could be true, don’t have to be true because we don’t know which sport–tennis or softball–Corinne will pursue.
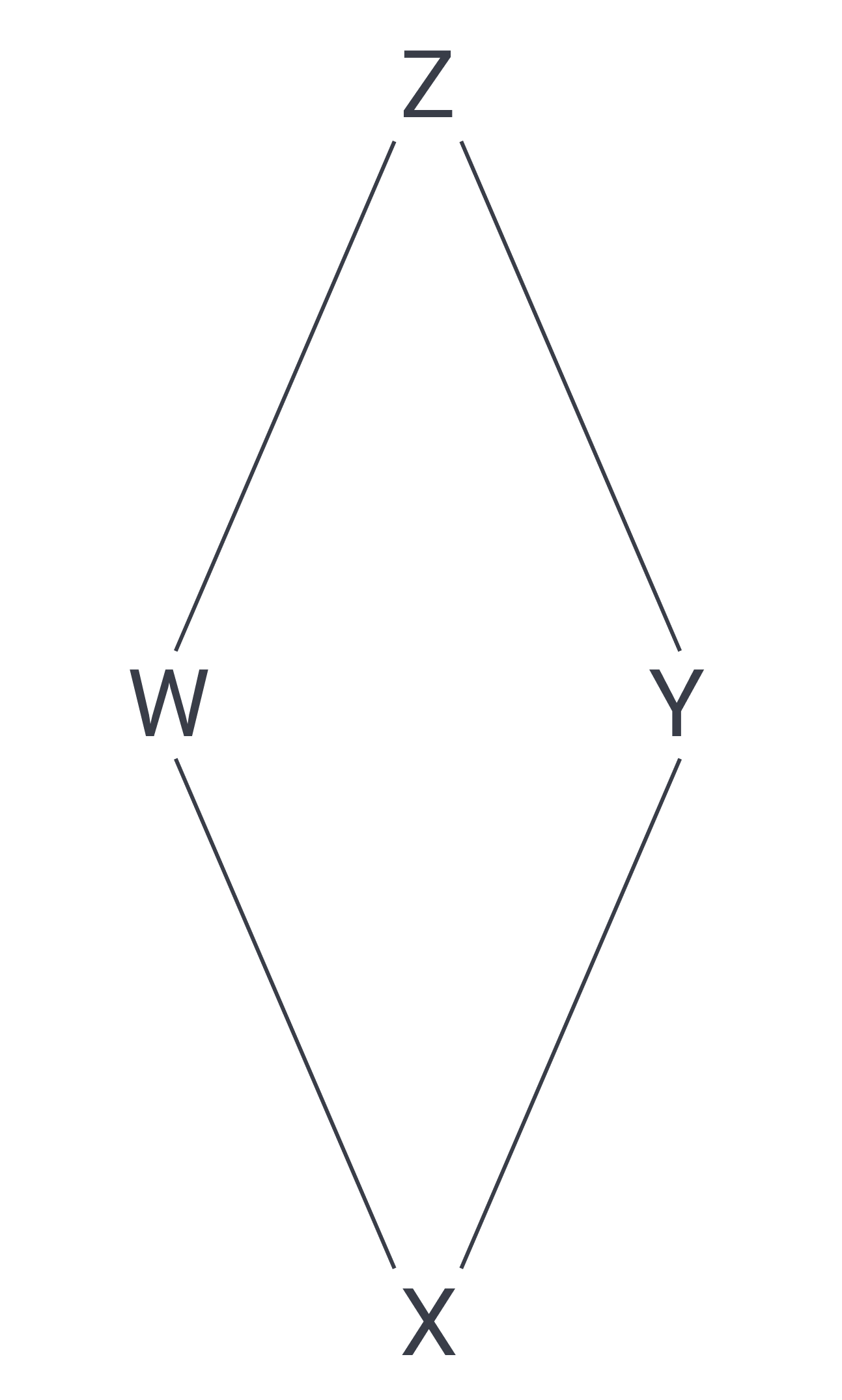
A researcher is determining the pH of four substances, W, X, Y, and Z. If substance W has a higher pH than substance X but a lower pH than substance Z, and if substance Y has a lower pH than substance W but a higher pH than substance X, then which of the following must be true?
I. Substance Z has a higher pH than substance W.
II. Substance Z has a higher pH than substance X.
III. Substance Z has a higher PH than substance Y.
A. III only
B. I and II only
C. II and III only
D. I, II, and III
The answer is D because all three statements are true. We can create a diagram that shows the relative pH’s vertically, where higher on the diagram is a higher page. The first relationship puts Z on top, then W, then X; the second adds that Y is also below Z and above X. The results look like this.
The European bee-eater is a migratory bird species except for its African population, which does not migrate. Migratory bee-eaters fly from Europe to Africa. Given this information, which of the following statements, if any, must be true?
A. If a European bee-eater is found in Africa, it must not be migratory.
B. If one encounters a migratory European bee-eater, one must be in Africa.
C. If a European bee-eater is encountered in Europe, it may be migratory or non-migratory.
D. None of the above must be true.
The answer is D because none of choices A, B, or C must be true. Choice A would be true of the non-migratory African population, but we also know that a European bee-eater currently in Africa could have flown there from Europe. Choice B might seem to fit with the idea of migration from Europe to Africa, but that doesn’t mean all the bee-eaters are currently in Africa. They might be just beginning their migration and still in Europe, or currently not migrating. Choice C could sound the most tempting because it seems to leave the options fairly open: couldn’t it be either kind of bird? Not in this case, because we are told all European bee-eaters are migratory … with the only exception being the African population. But if this African population does not migrate, it will never make it to Europe! If we see one of these birds in Europe, it would have to be migratory.
Some members of the band play the clarinet and most band members play more than one instrument. None of those who play more than one instrument fail to play the drums, but everyone who plays more than one instrument does not play the trombone. Finally, most band members are also in the orchestra. Which of the following must be true?
A. Some clarinet players in the band play more than one instrument.
B. No drummers also play the trombone.
C. Some trombone players also play the clarinet.
D. Some drummers only play the drums.
The answer is B. With a lot of information to keep track of, starting with the answers tends to work best. Must choice A be true, given what we know about clarinet players? Not necessarily, because the clarinet is never mentioned again after the first sentence establishing that the band has some clarinet players. What about choice C? Like choice A, it has the advantage of using the word “some”, which can often mark a correct answer because it helps us avoid extreme language. But, also like choice A, choice C mentions the clarinet. We simply don’t know enough about the clarinet to establish choice C. To understand choice D, we need to unpack the statement, “None of those who play more than one instrument fail to play the drums.” This is a double-negative meaning that if someone plays more than instrument, that person definitely plays the drums. We need to be careful and avoid falling for the converse; it is not necessarily true that if you play the drums, you play more than one instrument. There could be some drum players who only play the drums, but the problem is that we don’t know that to be the case. We have no proof one way or the other. That leaves choice B. Consider the statement, “Everyone who plays more than one instrument does not play the trombone.” If someone plays multiple instruments, none of those instruments can be the trombone. That means choice B must be true because if we encounter a drummer, we know that drummer can’t also play the trombone since that would make multiple instruments. Another way to put this is that, for whatever reason, trombone players are single-instrument people; they play nothing else.
Most Zorks are Sploinks, and some Sploinks are Quoozers. Also, all Zorks are Knoobs and some Zorks are not Quoozers. Which of the following must be true?
A. Most Zorks are Quoozers.
B. Some Sploinks are Knoobs.
C. Some Sploinks are not Knoobs.
D. Some Quoozers are not Zorks.
The answer is B. This question used nonsense words to challenge you to think about the underlying logic without your “real-life” sense kicking in. It’s a challenge to keep it straight! Let’s start with the group mentioned most: the Zorks. We seem to know a lot about them, do we know either choice A or choice D? More than half of the Zorks must also be Sploinks, and some of the Sploinks are Quoozers, but that doesn’t mean that these two groups of Sploinks overlap at all. (If you’re feeling confused by the wording and silly language, check out this Venn diagram to visualize the question’s first sentence.
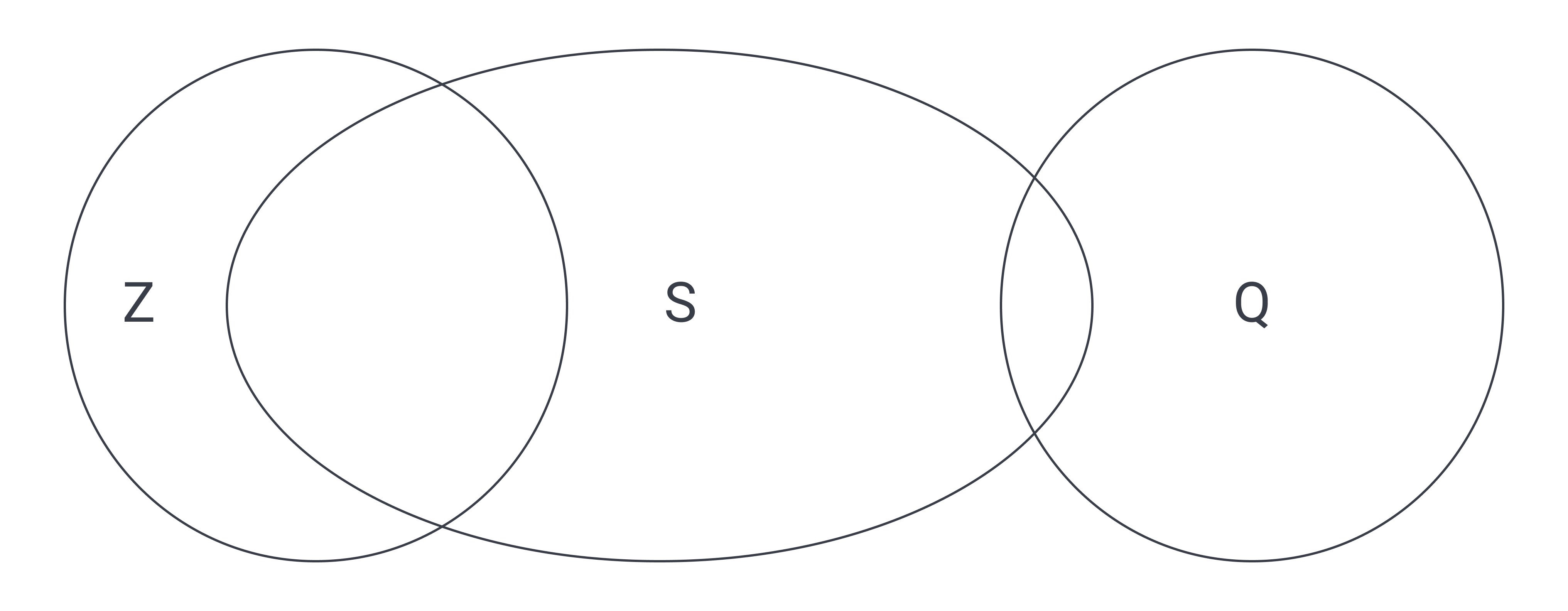This possible arrangement of Venn Diagram circles shows that, based on the first sentence, there doesn’t have to be any overlap at all between Z and Q. The second sentence doesn’t get us any further, despite comparing Z and Q directly. We know that some Z are not Q, but does that mean any Z are Q? We still don’t know.
The Venn Diagram above might seem to suggest that choice D is true, since the Q circle does not overlap with Z. But it’s equally possible that the entire Q circle is inside the Z circle; nothing prevents this. And even if it’s true that some Z are not Q, that doesn’t mean that some Q are not Z. Why not? Think of the Venn diagram comparing dogs and mammals. The “dog” circle will be entirely inside the “mammal” circle. So while it’s certainly true that there are some mammals that are not dogs, it doesn’t follow from this that some dogs are not mammals.
We are left with choices B and C. Since both compare K and S, let’s what we know about “Knoobs”. If all Z are K, then the Z circle must be entirely inside the K circle. That’s everything we know about Z, but let’s continue with K: we also know that most K are S. Consider the following diagram:
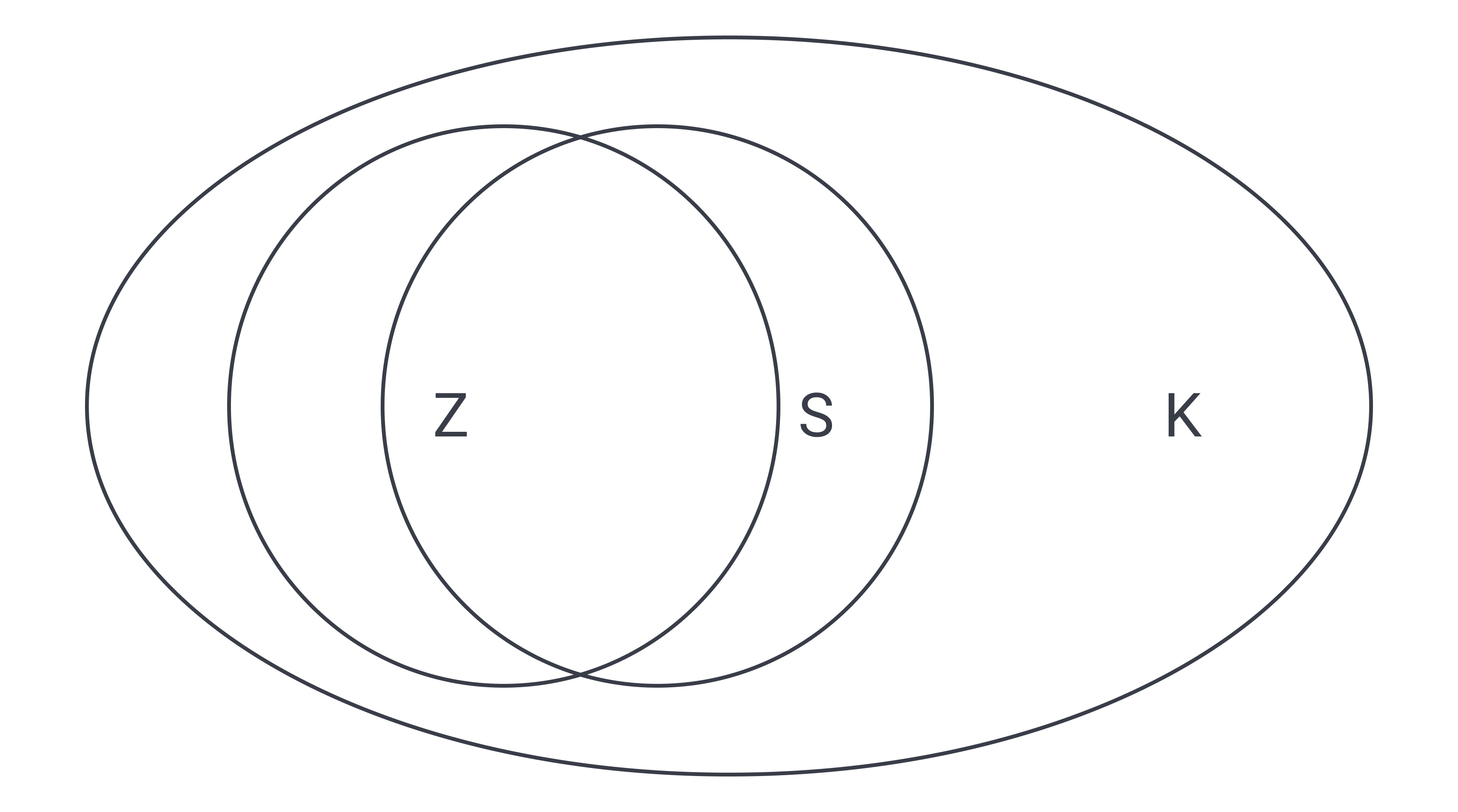
If Z is entirely inside K and predominantly inside S, then there must be some overlap between K and S. Choice B fits, while we could falsify choice C by looking at the diagram again: in this situation, at least, all the S are inside K, and this is a possible scenario, so choice C doesn’t have to be true.
Sign up for free to take 5 quiz questions on this topic