Yield
We first discussed the concept of yield in the preferred stock chapter. The concept is the same for bonds; yield measures the overall return of an investment. With bonds, several factors determine bond yields, including:
- The interest rate (coupon)
- The purchase price
- The length of time until maturity
While a bond’s interest rate and yield may sound like the same thing, they are not (except for the nominal yield, discussed below). The interest rate represents the annual interest paid by the issuer to the bondholder, while the yield represents the overall rate of return of the bond. A bond’s interest rate factors into its yield, but the interest rate and yield differ if it is bought at a discount or a premium.
We’ll discuss the following yields in this chapter:
- Nominal yield
- Current yield
- Yield to maturity (YTM)
- Yield to call (YTC)
Nominal yield
The nominal yield is another way to refer to the interest rate (coupon). You will likely never do a calculation to find the nominal yield, but you may be asked what the formula is.
For example:
A $1,000 par, 4% bond
As you can see, we went through a calculation only to find the 4% that was originally provided. The nominal yield is based on two factors, which never change. This bond has a $1,000 par value and pays $40 annually to its bondholder, regardless of what happens in the market. The nominal yield is a fixed, unaffected rate throughout the bond’s life. Unlike all the other yields we’ll discuss, the bond’s market price is not a factor.
Current yield
A bond’s current yield is a quick, easy, and not-so-terribly accurate way to calculate a bond’s overall rate of return. It factors in annual income and market price, but disregards time. Time is important for bonds, as it determines how long interest is paid and when the final principal payment is made. Therefore, many financial professionals use current yield as a quick and “sloppy” way to calculate yield but rarely provide it to clients (as it may be misleading).
Let’s add some information to the example we used in the last section.
A $1,000 par, 4% bond bought for $800
If this bond is bought at $800 (a discount), the bond’s overall return will be higher than the interest rate of the bond. How do we know this? The investor is earning two separate forms of return:
Coupon
- Pays the investor $40 annually
Discount
- Investor earns $200 over the life of the bond
The investor receives 4% of par ($1,000) annually but also benefits from the difference between the purchase price and the maturity value (par). The extra $200 return adds to their overall return (yield), so we can assume it’s something above 4%. The current yield is found by dividing the annual income by the security’s market price.
A $1,000 par, 4% bond bought for $800. What’s the current yield?
Can you figure it out?
As you can see, the current yield reflects a higher yield than the coupon. Therefore, you can always assume the current yield for discount bonds will always be higher than the coupon.
Let’s also discuss how current yield works with premium bonds. As a reminder, premium bonds trade in the market at prices above par ($1,000).
A $1,000 par, 4% bond bought for $1,100
The investor purchasing this bond will receive $40 a year in interest from the issuer. They’ll lose money over the bond’s life by buying it at a premium because bonds mature at par. They are paying $1,100 for a bond that will mature at $1,000, resulting in a $100 loss at maturity. Because of this dynamic, yields of premium bonds will always be lower than the coupon.
A $1,000 par, 4% bond bought for $1,100. What is the current yield?
Can you figure it out?
When the coupon is coupled with the loss of the premium, we find that the investor’s current yield reflects a more accurate rate of return than the coupon. Therefore, you can always assume the current yield for premium bonds will always be lower than the coupon.
Here’s a video breakdown of a practice question on current yield:
Yield to maturity (YTM)
Yield to maturity and yield to call formulas are difficult to memorize and typically are not tested. Exam questions are more likely to focus on the relationships of the yields, which is best depicted on the bond see-saw (discussed at the end of this chapter). Additionally, a test question may focus on the components of these yield formulas. Don’t spend much time focusing on the math related to these yields.
Unlike current yield, the yield to maturity (YTM) (also known as a bond’s basis) factors in time as it assumes the investor buys the bond and holds it until maturity. Additionally, it is a much more accurate representation of a bond’s overall rate of return. Let’s look at an example:
A 10 year, $1,000 par, 4% bond is trading at $800. What is the yield to maturity (YTM)?
The annual income is $40, based on the 4% coupon. The annualized discount is found by dividing the overall discount ($200) by the years until maturity (10). Remember, the discount equals the difference between the market price ($800) and par ($1,000). Then, find the average between the market price ($800) and par ($1,000).
This yield (6.7%) exceeds the coupon (4%). The trend remains the same; bonds bought at discounts have yields higher than their coupon because the bond’s discount provides an added return.
Let’s look at how YTM looks with a premium bond.
A 10 year, $1,000 par, 4% bond is trading at $1,100. What is the yield to maturity (YTM)?
The bond’s annual income is $40, based on its 4% coupon. The annualized premium is found by dividing the premium ($100) by the years to maturity (10 years). Instead of adding, we subtract the annualized premium because the investor is losing money over time. The average value of the bond is found by adding the market value ($1,100) to the par value ($1,000) and dividing by 2.
We see the trend again with premium bonds. The yield is lower than the bond’s coupon when purchased at a market price above par.
Yield to call (YTC)
Remember the advice above - the math behind the yield to call formula is unimportant.
Yield to call (YTC) only applies to callable bonds. If a bond is not callable, YTC does not exist. It represents a bond’s overall rate of return if held until the bond is callable. Essentially, we’re assuming the bond will be called as soon as it’s eligible. Like YTM, YTC also factors in time to its calculation. The YTC formula is similar to the YTM formula, but some differences exist.
A 10 year, $1,000 par, 4% bond is trading at $800. The bond is callable at par after 5 years. What is the yield to call (YTC)?
Again, we see the yield we calculated (8.9%) is higher than the coupon (4%). Also, the YTC (8.9%) is higher than the YTM (6.7%). Why is that? Remember, this investor is earning a discount of $200 over the bond’s life. If the bond is held to maturity, it takes the investor 10 years to make the $200 discount. If the bond is called in 5 years, the customer earns $200 5 years earlier than expected, increasing their annualized return rate.
Let’s take a look at YTC with a premium bond:
A 10 year, $1,000 par, 4% bond is trading at $1,100. The bond is callable at par after 5 years. What is the yield to call (YTC)?
We see the yield we calculated (1.9%) is lower than the coupon (4%). Also, the YTC (1.9%) is lower than the YTM (2.9%). Why is that? Remember, this customer is losing a premium of $100 over the bond’s life. If the bond is held to maturity, it takes the investor 10 years to lose the $100 premium. If the bond is called in 5 years, the customer loses the $100 5 years earlier than expected, which decreases their annualized rate of return.
Discount bond yield relationships
Let’s look at a summary of our discount bond example from the previous sections.
A 10 year, $1,000 par, 4% bond is trading at $800. The bond is callable at par after 5 years.
-
Coupon = 4.0%
-
Current yield = 5.0%
-
YTM = 6.7%
-
YTC = 8.9%
The order of these yields is no coincidence. Every discount bond will exhibit the same relationship. The coupon will be the lowest, followed by the current yield, then the YTM, and last the YTC. You could spend time calculating each yield separately or utilize a beloved visual with bonds: the bond see-saw.
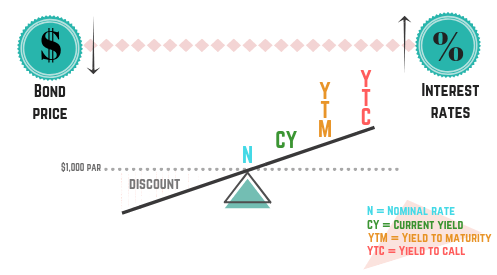
As you can see, the bond see-saw is a quick way of determining the relationship between a bond’s price and its yields. Many test-takers commit the bond see-saw to memory and write it on scratch paper when they take the exam. By doing this, you can avoid doing most of the calculations we just went through.
FINRA is more concerned that you know the relationship between the yields (which is lower or higher) than your ability to calculate these yields. While you certainly can be required to calculate current yield, the order of the yields and their relationships are more important topics to master. Plus, knowing the order of yields will help you eliminate wrong answers to yield calculation questions.
Premium bond yield relationships
Let’s continue using our premium bond example from the previous sections.
A 10 year, $1,000 par, 4% bond is trading at $1,100. The bond is callable at par after 5 years.
-
Coupon = 4.0%
-
Current yield = 3.6%
-
YTM = 2.9%
-
YTC = 1.9%
Again, the order of these yields is no coincidence. Every premium bond will exhibit the same relationship between the yields. The YTC will be the lowest, followed by the YTM, then the current yield, and last the coupon. You could spend time calculating each yield separately, or you can utilize the bond see-saw.
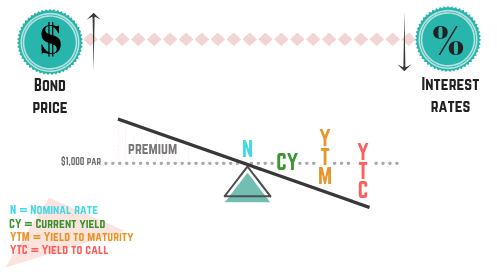
As we witnessed with discount bonds, the bond see-saw gives us a great visual representation of the yields. Now, we have the price side pointed upward, as premium bonds are purchased at prices above par. Remember the specific order of the yields on the see-saw, and yield-based questions will be easy to answer!
Yield for par bonds
We’ve reviewed how prices affect bonds’ yields purchased at discounts and premiums. What if a bond is purchased at par ($1,000)? We won’t need to go into much detail because this concept is fairly simple. When a bond is purchased at par, all of the yields are equal to the coupon. The investor isn’t making or losing any money through the purchase price of their bond. The bond is bought at par ($1,000) and will mature at par ($1,000). The only return the investor realizes is the coupon. For a bond purchased at its par value, the see-saw looks like this:
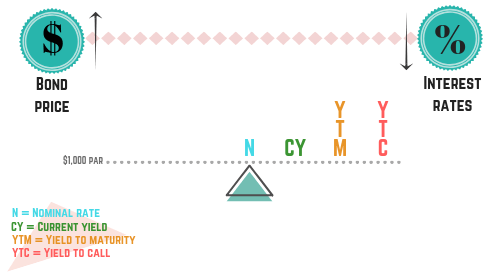
As you can see, the coupon is at the same level as the current yield, YTM, and YTC. If you see a question on par bond yields, keep it simple. All of them are the same.
The bond see-saw
Yield is a very important concept on the SIE exam, and the bond see-saw helps visualize the relationship between bond prices, interest rate changes, and yields. We’ve looked at the see-saw through the lens of a discount, premium, and par bond. Let’s take a look at all of them together:
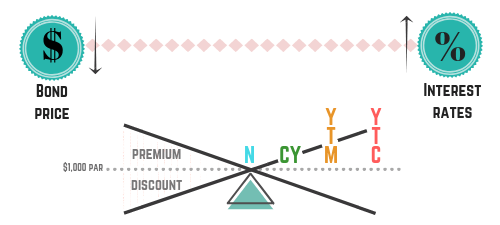
If you will utilize a “dump sheet,” it’s highly recommended that this be a part of it. A dump sheet is a list of visual items written on your scratch paper after you start your exam. Many students memorize concepts like the bond see-saw to rewrite them for the exam and rely on them for yield-based questions.
Additionally, many successful test-takers use acronyms like this:
CYM Call
-
CY = Current Yield
-
M = yield to Maturity
-
Call = yield to Call
Whatever will help you commit these terms to memory is encouraged. It doesn’t matter how you remember it, as long as you remember it!
Sign up for free to take 27 quiz questions on this topic