We first discussed the concept of yield in the preferred stock chapter. The idea is the same for bonds: yield measures the overall return of an investment. For bonds, yield is influenced by several factors, including:
A bond’s interest rate (coupon) and its yield sound similar, but they aren’t the same thing (except for nominal yield, discussed below). The interest rate is the annual interest the issuer pays based on par value. Yield is the bond’s overall rate of return, which depends on both the coupon and the price you pay. If a bond is purchased at a discount or a premium, its yield will differ from its coupon.
We’ll discuss the following yields in this chapter:
The nominal yield is another name for the bond’s interest rate (coupon). You’ll rarely calculate nominal yield in practice, but you may be asked to identify the formula.
For example:
A $1,000 par, 4% bond
This calculation simply confirms the stated 4% coupon. Nominal yield depends on two values that don’t change:
No matter what happens to the bond’s market price, the issuer still pays $40 per year, and the bond still matures at $1,000. That’s why nominal yield stays fixed over the bond’s life. Unlike the other yields in this chapter, market price is not part of the nominal yield calculation.
A bond’s current yield is a quick (but incomplete) way to estimate return. It uses annual income and the bond’s current market price, but it ignores time. Time matters for bonds because it affects:
Because of that, current yield is often used as a fast approximation, but it can be misleading if treated as a full measure of return.
Let’s add market price to the example.
A $1,000 par, 4% bond bought for $800
If this bond is bought at $800 (a discount), the investor’s overall return will be higher than the 4% coupon. That’s because the investor earns return from two sources:
Coupon
Discount
The investor receives 4% of par ($1,000) each year, and also benefits from the bond moving from the purchase price ($800) up to par ($1,000) at maturity. That extra $200 increases the overall return.
Current yield is calculated by dividing annual income by the bond’s market price.
A $1,000 par, 4% bond bought for $800. What’s the current yield?
Can you figure it out?
Because the bond is purchased at a discount, the current yield (5%) is higher than the coupon (4%). So you can assume:
Now compare that to a premium bond. Premium bonds trade above par.
A $1,000 par, 4% bond bought for $1,100
The investor still receives $40 per year in interest. But because the bond matures at par, paying $1,100 for a bond that will be worth $1,000 at maturity creates a $100 loss over time. That pushes the overall return below the coupon.
A $1,000 par, 4% bond bought for $1,100. What is the current yield?
Can you figure it out?
Here, the current yield (3.6%) is lower than the coupon (4%). So you can assume:
Here’s a video breakdown of a practice question on current yield:
Yield to maturity and yield to call formulas are difficult to memorize and typically are not tested. Exam questions are more likely to focus on the relationships of the yields, which is best depicted on the bond see-saw (discussed at the end of this chapter). Additionally, a test question may focus on the components of these yield formulas. Don’t spend much time focusing on the math related to these yields.
Unlike current yield, yield to maturity (YTM) (also called a bond’s basis) includes time. It assumes the investor buys the bond and holds it until maturity, making it a more complete measure of overall return.
A 10 year, $1,000 par, 4% bond is trading at $800. What is the yield to maturity (YTM)?
Here’s what each part represents:
The YTM (6.7%) is higher than the coupon (4%). That matches the general pattern: discount bonds have yields above the coupon because the discount adds to return.
Now compare a premium bond.
A 10 year, $1,000 par, 4% bond is trading at $1,100. What is the yield to maturity (YTM)?
The YTM (2.9%) is lower than the coupon (4%), which is the typical premium-bond relationship.
Remember the advice above - the math behind the yield to call formula is unimportant.
Yield to call (YTC) applies only to callable bonds. If a bond isn’t callable, there is no YTC.
YTC is the bond’s overall rate of return assuming it’s called at the first call date. Like YTM, it includes time. The formula is similar to YTM, but it uses:
A 10 year, $1,000 par, 4% bond is trading at $800. The bond is callable at par after 5 years. What is the yield to call (YTC)?
The YTC (8.9%) is higher than the coupon (4%), and it’s also higher than the YTM (6.7%). The reason is timing: the investor earns the $200 discount sooner.
Now look at a premium bond.
A 10 year, $1,000 par, 4% bond is trading at $1,100. The bond is callable at par after 5 years. What is the yield to call (YTC)?
The YTC (1.9%) is lower than the coupon (4%), and it’s also lower than the YTM (2.9%). Again, timing explains it:
Let’s summarize the discount bond example from the previous sections.
A 10 year, $1,000 par, 4% bond is trading at $800. The bond is callable at par after 5 years.
Coupon = 4.0%
Current yield = 5.0%
YTM = 6.7%
YTC = 8.9%
This ordering is consistent for discount bonds:
Instead of calculating each yield, many test-takers rely on a visual tool: the bond see-saw.
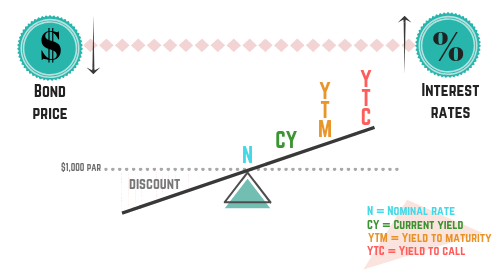
The bond see-saw is a fast way to determine how price relates to yields. Many people memorize it and rewrite it on scratch paper at the start of the exam.
FINRA is more focused on whether you understand which yield is higher or lower than on whether you can compute every yield. You may still need to calculate current yield, but yield relationships are tested frequently. Knowing the order also helps you eliminate incorrect answer choices.
Let’s continue using the premium bond example from the previous sections.
A 10 year, $1,000 par, 4% bond is trading at $1,100. The bond is callable at par after 5 years.
Coupon = 4.0%
Current yield = 3.6%
YTM = 2.9%
YTC = 1.9%
This ordering is consistent for premium bonds:
You can calculate each yield, or you can use the bond see-saw.
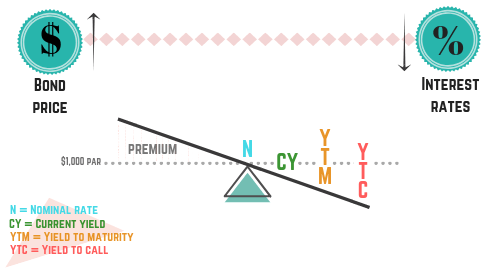
For premium bonds, the price side points upward because the bond trades above par. The yield side points downward, reflecting that yields are below the coupon.
We’ve seen how discounts and premiums affect yield. What if a bond is purchased at par ($1,000)? This case is straightforward.
When a bond is purchased at par:
So, all yields equal the coupon.
For a bond purchased at par, the see-saw looks like this:
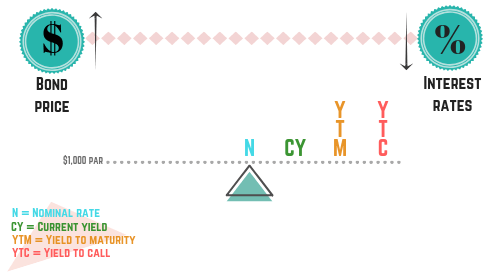
Coupon, current yield, YTM, and YTC all line up at the same level. If you see a question about par bond yields, keep it simple: they’re all the same.
Yield is a major SIE topic, and the bond see-saw helps you visualize the relationship between bond prices, interest rate changes, and yields. Here are the discount, premium, and par versions together:
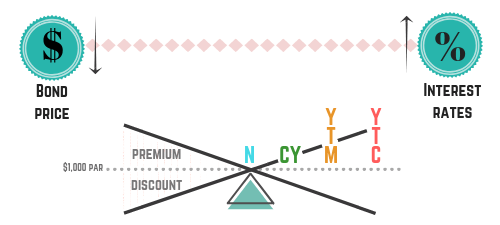
If you use a “dump sheet,” this is a common item to include. A dump sheet is a set of key visuals or facts you write on scratch paper after the exam begins, so you can reference them during questions.
Some test-takers also use acronyms like this:
CYM Call
CY = Current Yield
M = yield to Maturity
Call = yield to Call
Use any memory aid that helps you keep the yield terms and their order straight.
Sign up for free to take 27 quiz questions on this topic