The UnCLES Method for CLT Math

UnCLES Explained

Understand important phrases or indicators. Words such as diameter, even, tangent, integer, and isosceles are all examples of terms to note carefully. Write such terms on your scratch paper near where you’re solving the problem. The purpose of this step is to make sure that you don’t overlook crucial details for solving.

Clarify exactly what the problem is asking for. If there is any potential uncertainty about what you’re solving for, write down the precise wording of the question on your scratch paper. If the problem asks you to find $x^{2}$ , then make sure you don’t stop when you solve for $x$ ! The purpose of this step is to make sure you solve for the right value, variable, or expression.

Look at the answers before you start solving. To identify patterns among the answer choices, imagine that the answer choices are part of a topical list. How would you title that list? Positive numbers? Negative numbers? Variable expressions? Also, pay attention to how the answers are formatted. For example, are they left in expanded form or completely simplified? Do they have a common denominator? What other similarities and differences do you observe? The purpose of this step is to provide clues about how to answer the question efficiently.

Establish your solution strategy. Before you start to solve, decide how you are going to solve the problem. Some basic strategies are: If it’s an ALGEBRA question, write an equation. If it’s a GEOMETRY question, draw a figure. If it’s a WORD PROBLEM, write an equation. If you can’t think of an efficient method, PLUG IN NUMBERS or BACKSOLVE (plug in the answers). The purpose of this step is to make sure you have a game plan for solving the problem.

Solve carefully and methodically, with the answer choices in mind. You may finish the process early because you recognize the answer from the multiple choice, but don’t skip steps along the way. Forgetting even the smallest step can completely wreck your work on the entire question. The purpose of this step is to help reduce careless errors in your work.

UnCLES Illustrated

Understand key terms.

What: As you are reading, understand important phrases or indicators. Pay attention to any word that completely changes the meaning of the question such as diameter, even, tangent, integer, and isosceles. Write such terms on your scratch paper near where you’re solving the problem.

Why: The purpose of this step is to make sure that you don’t overlook crucial details for solving the problem.

Example: A certain stock goes down by two points every day for the first week (note: the stock market only runs on weekdays); it doubles the following week; then it increases by 20 points the week after. If the stock starts at a value of x, which of the following expressions represents the value of the stock after these 3 weeks?

Execution: Write down or abbreviate all the words and phrases underlined above. Your notations might look something like this:

2↓/day
5 days
↑20
starts at x

Clarify the question.

What: When reading the question, identify exactly what you are solving for and, if there is any potential uncertainty, write down the word or phrase. Be concise. If the problem asks you to find $x^{2}$ , then make sure you don’t stop when you solve for $x$ . Remember that one of the most common errors on standardized tests is solving for the wrong quantity.

Why: The purpose of this step is to make sure you solve for the right value, variable, or expression.

Execution: A brief phrase on your scratch paper will do: something like “stock’s value at the end”. You can decide whether to write down the word “expression”; one advantage of doing so is that it reminds you you’re not looking for a full equation with an “equals” sign.

Look at the answers.

What: Before you start doing work, look at the answer choices. Pay attention to the format of the answer choices to ensure that your final solution matches the answer choice format. Additionally, try to identify patterns among the answer choices. Pay attention to number properties such as positive/negative or even/odd, to multiples of the same number, and to closeness of answer choices, etc. Common properties among answer choices might give you a clue to solving the question.

Why: The purpose of this step is to provide clues about how to answer the question efficiently and give you an edge for guessing the answer if needed.

Example:

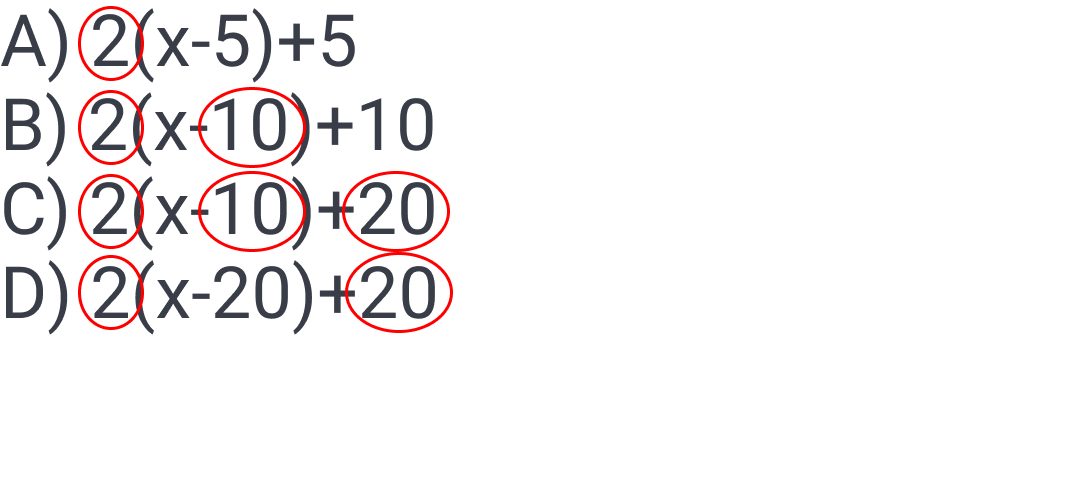
A B C D answer with patterns identified

Establish your strategy.

What: Before you start to solve, decide how you are going to solve the problem. Some basic strategies are: if it’s an ALGEBRA question, write an equation. If it’s a GEOMETRY question, draw a figure. If it’s a WORD PROBLEM, write an equation. If you can’t think of an efficient method, PLUG IN NUMBERS or BACKSOLVE (plug in the answers).

Why: The purpose of this step is to make sure you have a game plan for solving the problem.

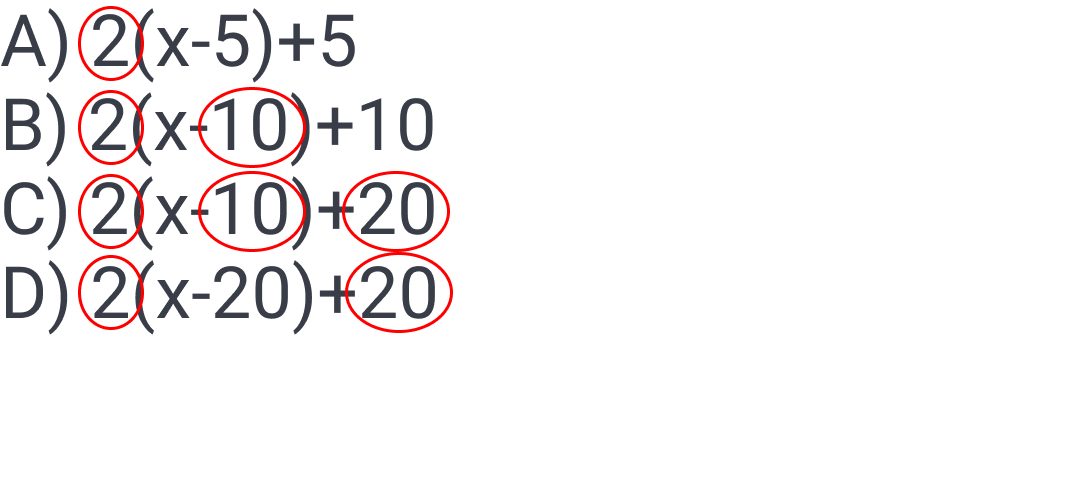
A B C D answer with patterns identified

As is often the case, two possible solution strategies emerge with this problem, based on our understanding of key terms, clarifying of the question, and careful review of the answers:

As noted above, If it’s a word problem, write an equation. In this case we have an expression rather than an equation (no equals sign), but the idea is the same. We may decide to take each key part of the word problem and “translate” it into algebra. See the step below for the execution.
For the sake of efficiency, we can also work backward from the answers. This “backsolving” strategy shouldn’t be considered simply a last resort; it can sometimes be a faster (and therefore better) way to solve a CLT problem. See below for how it works.

Solve carefully and methodically with the answers in mind.

What: Solve carefully, showing your steps! Make sure you even show the simple steps. Forgetting even the smallest step can completely wreck your work on the entire question.

Why: The purpose of this step is to help reduce careless errors in your work.

Here is Strategy 1, “translating” from math to algebra, explained:

We take the three elements we underlined and translate them into math: a “ $2$ ” in front for “doubles,” a “ $+ 20$ ” at the end for “increases by 20 points,” and (this is the hardest part) a “ $- 10$ ” for “down by two points every day” plus “weekdays”—details which, together, tell us that we need to multiply 2 by 5 and subtract the result.

Here’s Strategy 1 in a more step-by-step format that might represent what you write on your scratch paper:

STEP 1: “Doubles” means I need a $2$ at the beginning multiplied by something: $2 (...$
STEP 2: What is doubled? The first week’s total, so I need to think about that. Dropping by 2 over 5 days would subtract 10, and the unknown starting point could be called $x$ ; so far, I have:

$2 (x - 10)$

STEP 3; I need to incorporate what happens in the second week, when it “increases by 20.” That only happens once, so I can add it as a constant at the end:

$2 (x - 10) + 20$

Here’s Strategy 2, explained:

Every answer begins with a 2, so that doesn’t help us eliminate anything on that basis.

So we look at other differences: two of the answers have $- 10$ ; not only is this likely correct because the majority of the answers have it, but it also fits a 2-point drop per day over five days. So answers A and D are eliminated.

Finally, we compare the final parts of answers B and C and ask ourselves which matches; choice B’s $+ 10$ does not match “increases by 20,” so choice B is out.

And for Strategy 2, in which you work backward from the answers, showing your work would involve writing “A”, “B”, “C”, and “D” vertically down on your page and eliminating the answers one by one, so first:

A)
B)
C)
D)

Then:

A)
B)
C)
D)

The UnCLES Method for CLT Math

UnCLES Explained

UnCLES Illustrated

Answer C remains.