If you can break a problem down into several smaller (easier) pieces, you should. Always.
A common way to do that is to notice that a situation can be divided up into a few different cases. For example, you might notice that there are only three different ways a situation can unfold. So, you might consider those three situations – those three cases – separately. Congratulations! You’ve just turned a problem into three easier problems. That’s always better.
Here’s a problem where casing is a great approach:
How many paths from to consist of exactly six line segments (vertical, horizontal, or inclined)?
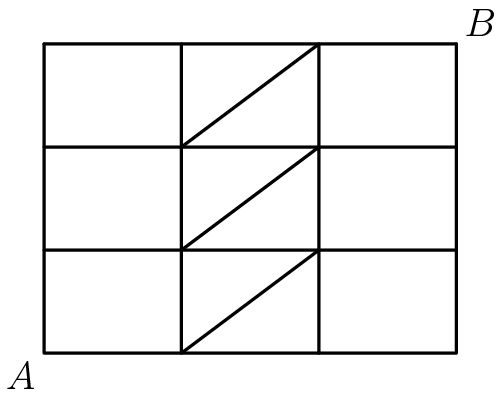
First, ignore the diagonal segments for a moment. Consider: at each vertex, you have the choice of going either up or to the right. (If you ever go left or down, then you won’t be able to make it to the end in just six segments.) Okay, so then each path can be described as a six-move list of ups and rights in some particular order. For example, up, right, right, up, up, right is a valid and unique path. But note also that this path must contain exactly three ups and exactly three rights. Have we seen something like this before? Maybe, yeah: this is the same problem as “how many ways can you combine three As and three Bs to make a six-letter nonsense word?”
The answer to that question is the same as the answer to the question of “how many paths are there here, ignoring the diagonals?” which is
Traversing the diagonals, we quickly find that the path must run through exactly 2 diagonals. There are pairs of diagonals through which this is possible; quick counting shows us that each pair of diagonals yields 2 paths. So there are 6 more cases here.
In total, we get paths.
Sign up for free to take 1 quiz question on this topic